문제
N x M 크기의 행렬 모양의 게임 맵이 있습니다. 이 맵에는 내구도를 가진 건물이 각 칸마다 하나씩 있습니다. 적은 이 건물들을 공격하여 파괴하려고 합니다. 건물은 적의 공격을 받으면 내구도가 감소하고 내구도가 0이하가 되면 파괴됩니다. 반대로, 아군은 회복 스킬을 사용하여 건물들의 내구도를 높이려고 합니다.
적의 공격과 아군의 회복 스킬은 항상 직사각형 모양입니다.
예를 들어, 아래 사진은 크기가 4 x 5인 맵에 내구도가 5인 건물들이 있는 상태입니다.
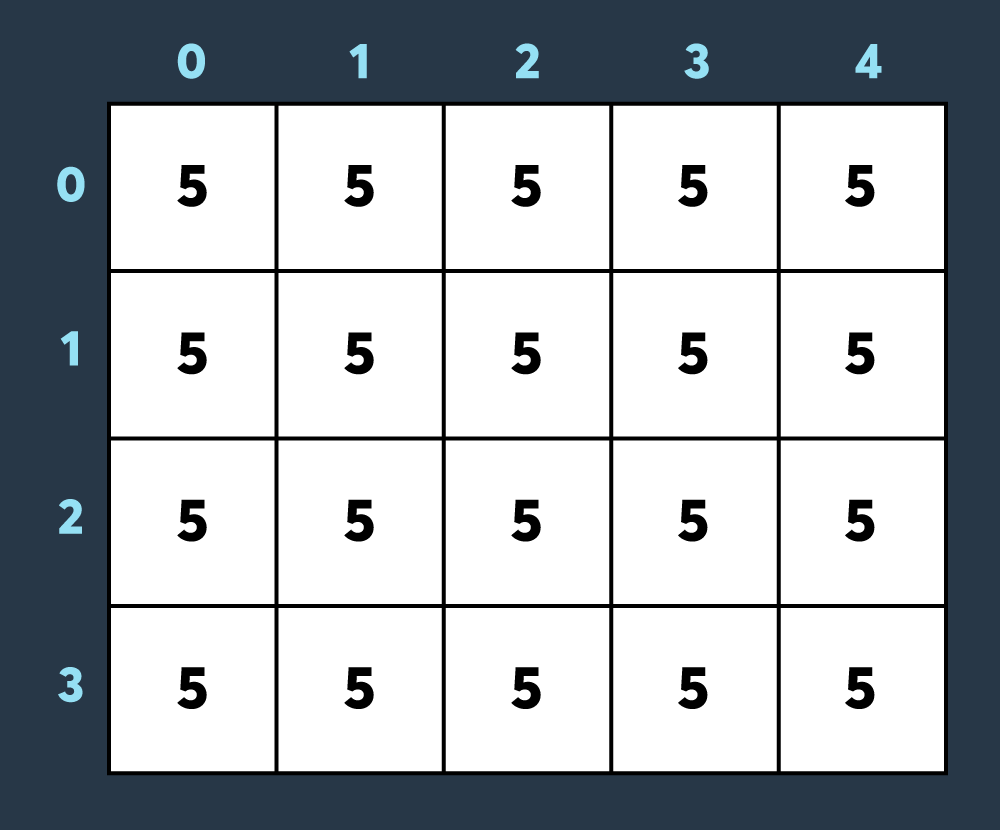
첫 번째로 적이 맵의 (0,0)부터 (3,4)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.
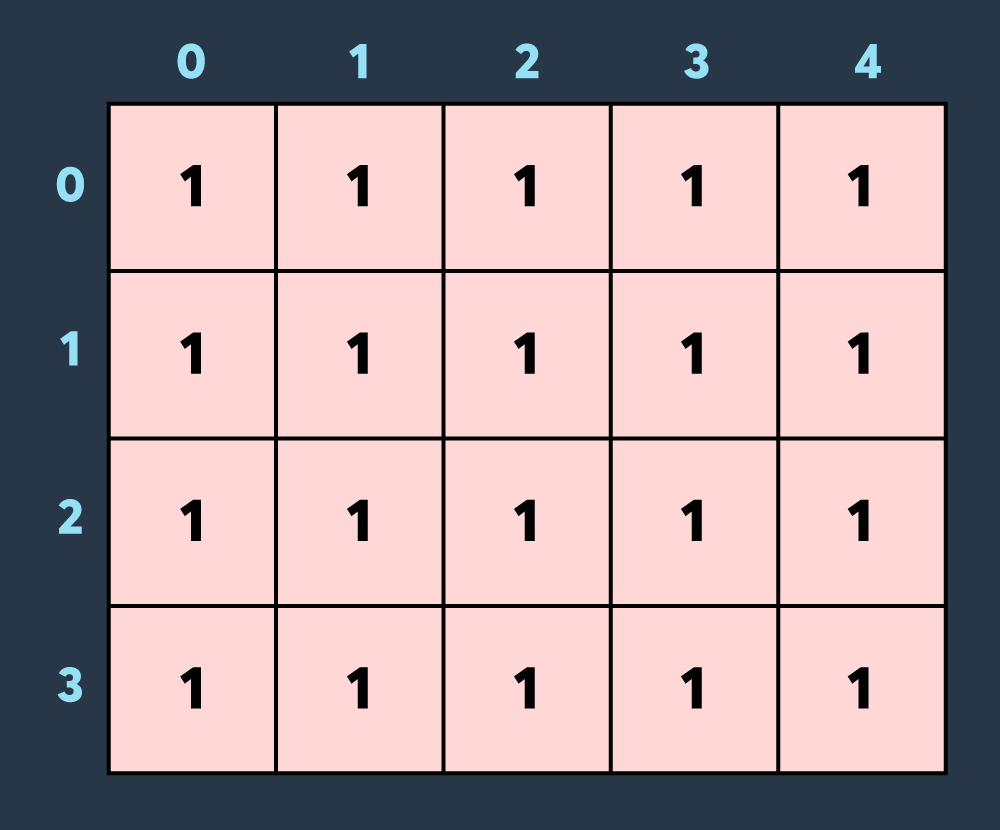
두 번째로 적이 맵의 (2,0)부터 (2,3)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같이 4개의 건물이 파괴되는 상태가 됩니다.
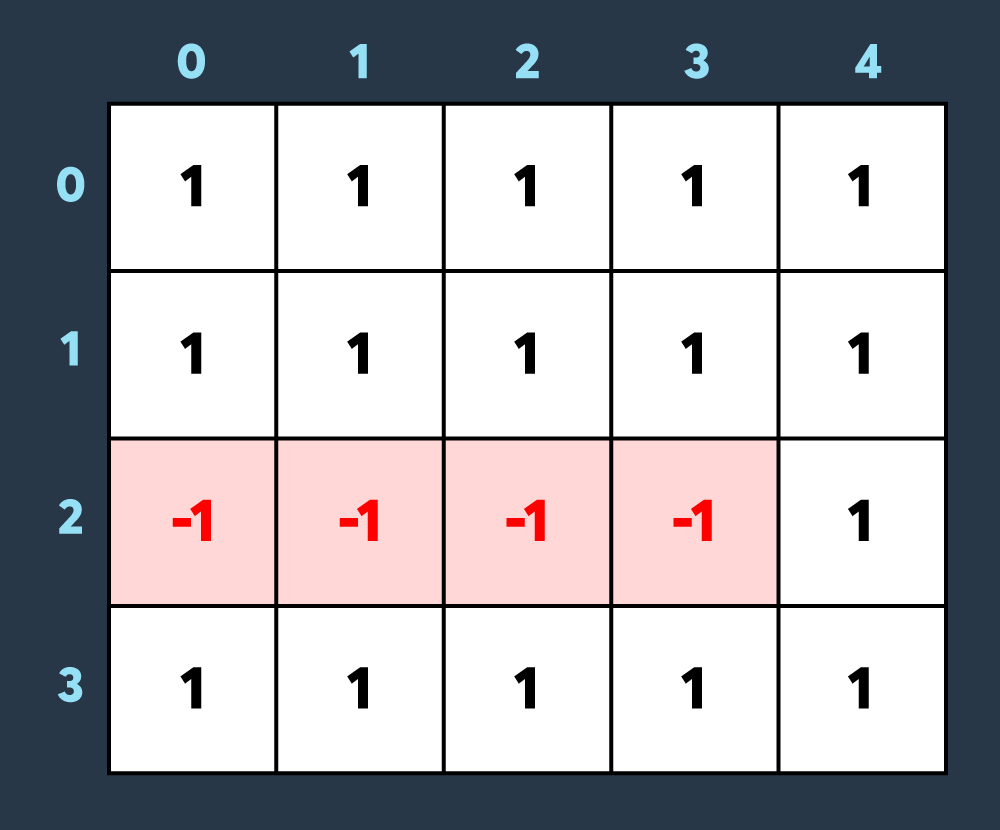
세 번째로 아군이 맵의 (1,0)부터 (3,1)까지 회복하여 2만큼 건물의 내구도를 높이면 아래와 같이 2개의 건물이 파괴되었다가 복구되고 2개의 건물만 파괴되어있는 상태가 됩니다.
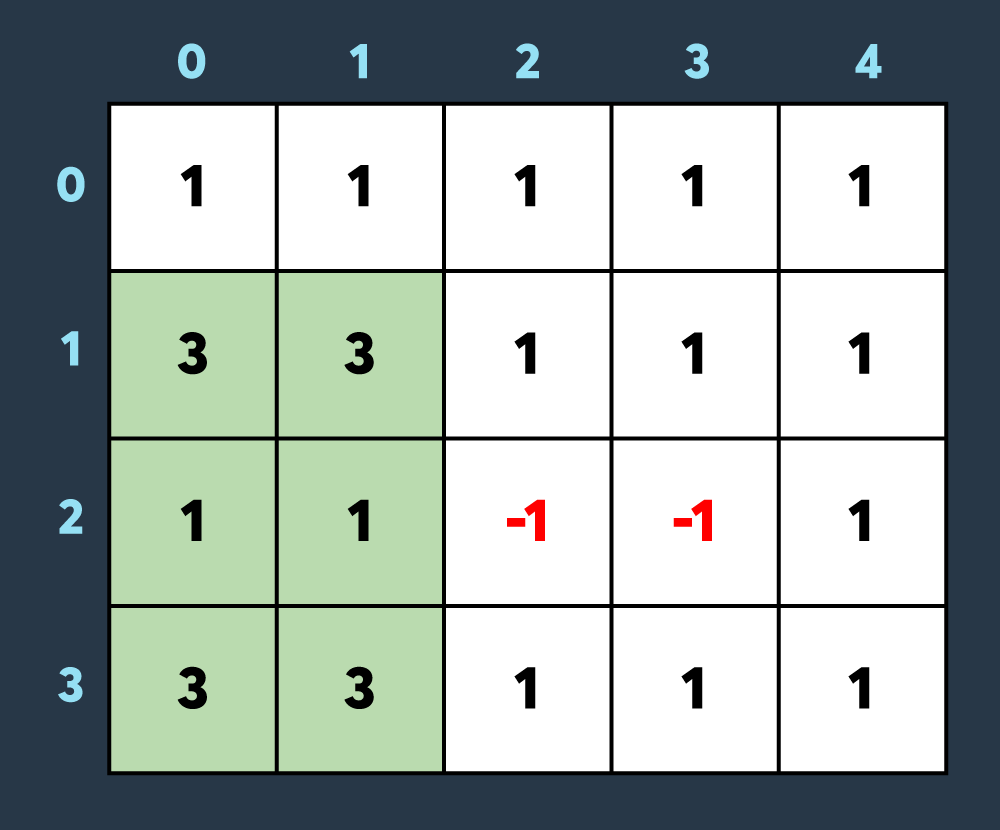
마지막으로 적이 맵의 (0,1)부터 (3,3)까지 공격하여 1만큼 건물의 내구도를 낮추면 아래와 같이 8개의 건물이 더 파괴되어 총 10개의 건물이 파괴된 상태가 됩니다. (내구도가 0 이하가 된 이미 파괴된 건물도, 공격을 받으면 계속해서 내구도가 하락하는 것에 유의해주세요.)
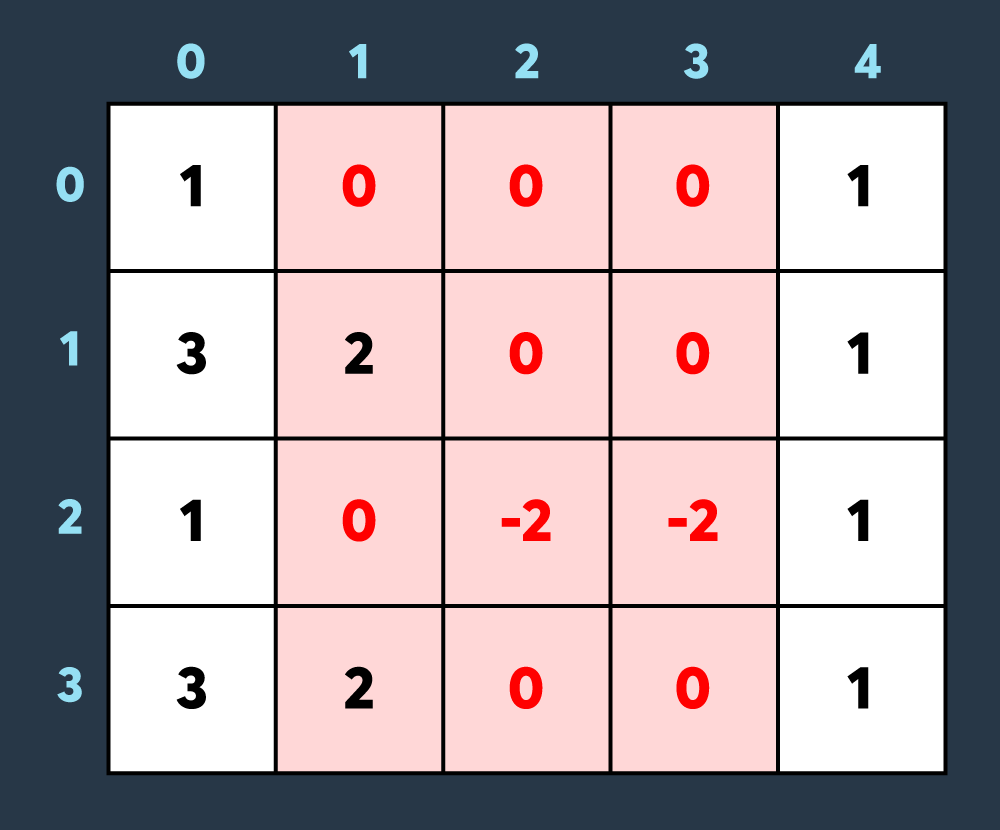
최종적으로 총 10개의 건물이 파괴되지 않았습니다.
건물의 내구도를 나타내는 2차원 정수 배열 board와 적의 공격 혹은 아군의 회복 스킬을 나타내는 2차원 정수 배열 skill이 매개변수로 주어집니다. 적의 공격 혹은 아군의 회복 스킬이 모두 끝난 뒤 파괴되지 않은 건물의 개수를 return하는 solution함수를 완성해 주세요.
제한사항
- 1 ≤ board의 행의 길이 (= N) ≤ 1,000
- 1 ≤ board의 열의 길이 (= M) ≤ 1,000
- 1 ≤ board의 원소 (각 건물의 내구도) ≤ 1,000
- 1 ≤ skill의 행의 길이 ≤ 250,000
- skill의 열의 길이 = 6
- skill의 각 행은 [type, r1, c1, r2, c2, degree]형태를 가지고 있습니다.
- type은 1 혹은 2입니다.
- type이 1일 경우는 적의 공격을 의미합니다. 건물의 내구도를 낮춥니다.
- type이 2일 경우는 아군의 회복 스킬을 의미합니다. 건물의 내구도를 높입니다.
- (r1, c1)부터 (r2, c2)까지 직사각형 모양의 범위 안에 있는 건물의 내구도를 degree 만큼 낮추거나 높인다는 뜻입니다.
- 0 ≤ r1 ≤ r2 < board의 행의 길이
- 0 ≤ c1 ≤ c2 < board의 열의 길이
- 1 ≤ degree ≤ 500
- type이 1이면 degree만큼 건물의 내구도를 낮춥니다.
- type이 2이면 degree만큼 건물의 내구도를 높입니다.
- type은 1 혹은 2입니다.
- 건물은 파괴되었다가 회복 스킬을 받아 내구도가 1이상이 되면 파괴되지 않은 상태가 됩니다. 즉, 최종적으로 건물의 내구도가 1이상이면 파괴되지 않은 건물입니다.
정확성 테스트 케이스 제한 사항
- 1 ≤ board의 행의 길이 (= N) ≤ 100
- 1 ≤ board의 열의 길이 (= M) ≤ 100
- 1 ≤ board의 원소 (각 건물의 내구도) ≤ 100
- 1 ≤ skill의 행의 길이 ≤ 100
- 1 ≤ degree ≤ 100
효율성 테스트 케이스 제한 사항
주어진 조건 외 추가 제한사항 없습니다.
입출력 예
| board | skill |
|---|---|
| [[5,5,5,5,5],[5,5,5,5,5],[5,5,5,5,5],[5,5,5,5,5]] | [[1,0,0,3,4,4],[1,2,0,2,3,2],[2,1,0,3,1,2],[1,0,1,3,3,1]] |
| [[1,2,3],[4,5,6],[7,8,9]] | [[1,1,1,2,2,4],[1,0,0,1,1,2],[2,2,0,2,0,100]] |
입출력 예 설명
- 입출력 예 #1
문제 예시와 같습니다. - 입출력 예 #2
<초기 맵 상태>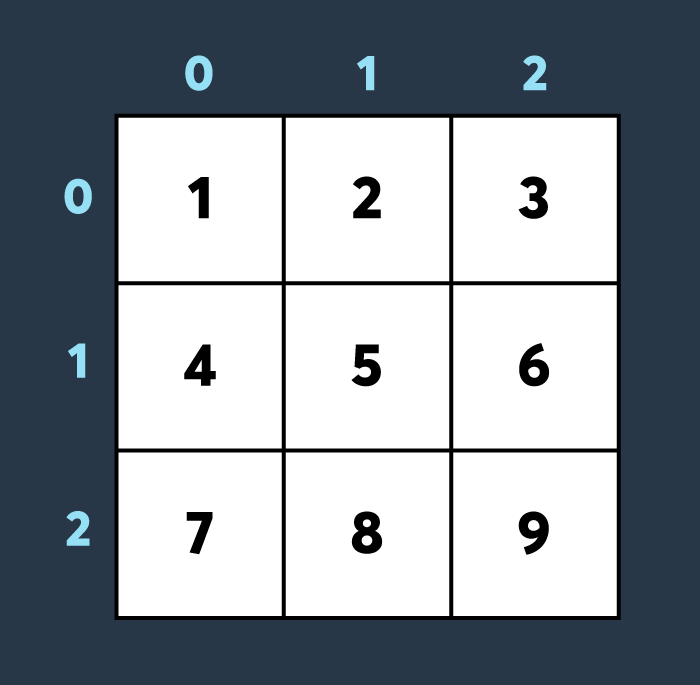
첫 번째로 적이 맵의 (1,1)부터 (2,2)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.
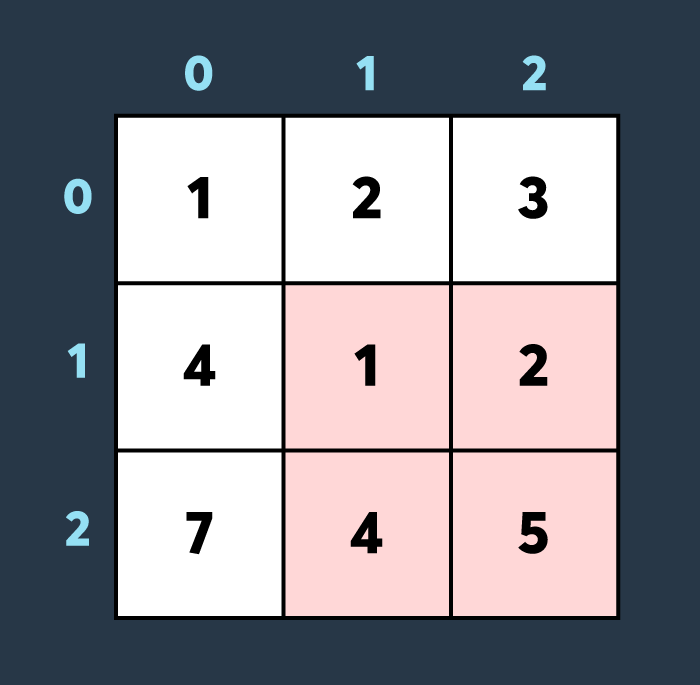두 번째로 적이 맵의 (0,0)부터 (1,1)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.
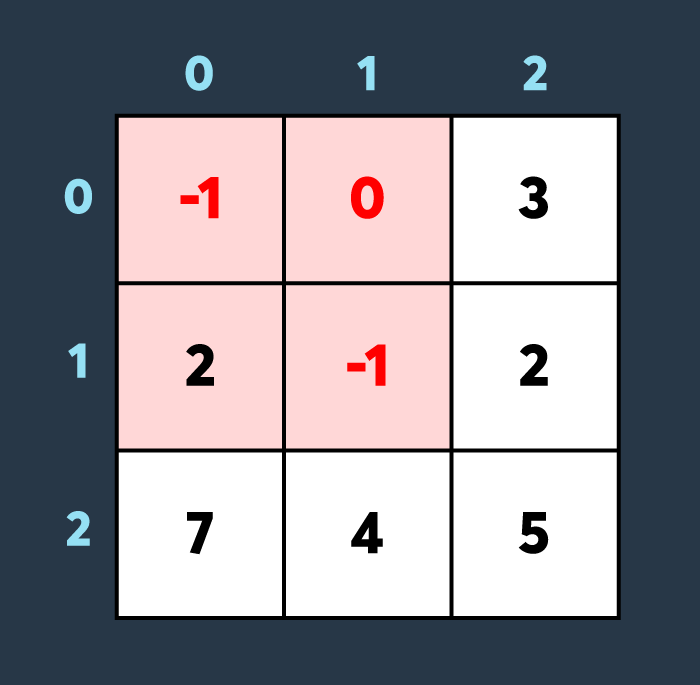마지막으로 아군이 맵의 (2,0)부터 (2,0)까지 회복하여 100만큼 건물의 내구도를 높이면 아래와 같은 상황이 됩니다.
풀이
설계
최초에는 단순 구현으로 skill에 주어진 명령어대로 이중 for문을 순회하며 값을 변경하는 방식으로 진행하였다. 그러나 이 케이스는 예상대로 효율성 테스트를 전혀 통과하지 못하였고, 질문 게시판을 통해 '누적합' 방식으로 구현하는 방법을 확인하였다.
누적합 방식의 경우 여전히 그 원리를 제대로 이해하고 있지는 못하지만, 전체 프로세스를 간단히 정리하면 다음과 같다.
-
0으로 구성된, board보다 가로세로가 1칸씩 더 큰 2차원 행렬(attack)을 선언한다.
-
skill type에 따라 degree의 값에 -를 곱하거나 그대로 두어 이를 변수 operation에 저장한다.
-
operation을 attack에 더하되, 다음과 같은 규칙에 따라 더한다.
- (r1, c1)에는 operation의 값을 더한다.
- (r2+1, c1)에는 operation의 값을 제한다.
- (r1, c2+1)에도 operation의 값을 제한다.
- (r2+1, c2+1)에는 다시 operation의 값을 더한다.
즉 m x n에 대한 공격 혹은 수리 명령이 입력되었을 때 각각의 m+1 x n+1 크기의 면에 대하여 각 꼭짓점에 공격 혹은 수리 명령의 수치를 더하거나 제하는 것인데, 좌측 상단 꼭짓점과 우측 하단 꼭짓점은 수치를 더하고, 우측 상단 꼭짓점과 좌측 하단 꼭짓점에는 수치를 제하는 것이다. 이렇게 함으로써 가장 마지막에 누적합 연산을 했을 때 원하는 구간에만 수치가 입력되도록 할 수 있다.
-
모든 operation의 입력이 완료되면, 다음과 같이 누적합 연산을 수행한다.
- 각 행의 왼쪽 끝에서부터 오른쪽으로 1칸씩 이동하며 이전 위치의 값을 더한다.
- 각 열의 상단에서부터 하단으로 1칸씩 이동하며 이전 위치의 값을 더한다.
-
attack의 요소들을 board에 더하여 최종 내구도를 계산하고, 0 을 초과하는 요소들의 총합을 반환한다.
코드
-
1차 코드 - 단순 구현
def solution(board, skills): for skill in skills: skill_type, r1, c1, r2, c2, degree = skill if skill_type == 1: for i in range(r1, r2+1): for j in range(c1, c2+1): board[i][j] -= degree elif skill_type == 2: for i in range(r1, r2+1): for j in range(c1, c2+1): board[i][j] += degree return len([x for x in sum(board, []) if x > 0]) -
2차 코드 - 누적합 구현
def solution(board, skills): max_r, max_c = len(board), len(board[0]) attack = [[0] * (max_c+1) for _ in range(max_r+1)] for skill in skills: skill_type, r1, c1, r2, c2, degree = skill operation = (-1) * degree if skill_type == 1 else degree attack[r1][c1] += operation attack[r2+1][c1] -= operation attack[r1][c2+1] -= operation attack[r2+1][c2+1] += operation for r in range(len(board)+1): for c in range(1, len(board[0])+1): attack[r][c] += attack[r][c-1] for c in range(len(board[0])+1): for r in range(1, len(board)+1): attack[r][c] += attack[r-1][c] return sum([1 if 0 < board[r][c] + attack[r][c] else 0 for r in range(max_r) for c in range(max_c)])
본 문제의 해결 방향과 누적합의 개념에 대해서는 다음 두 글이 도움이 되었다.
https://school.programmers.co.kr/questions/25471
https://school.programmers.co.kr/questions/30876
...물론 도움이 되었을 뿐 이해가 됐다는 말은 아닙니....
