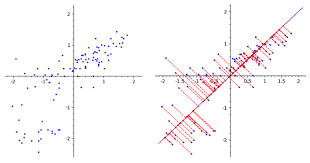
PCA란?

• 차원축소 기법중 하나로 원데이터의 성질을 유지하면서 여러개의 feature들을 dimention reduction을 하여 feature간의 경향성을 파악하고, 주성분을 만들어 낸다.

주성분: 기존의 변수를 조합하여 서로 연관성이 없는 새로운 변수

등장배경

고차원의 데이터는 계산과 시각화가 어려워 분석하기가 쉽지 않다.

따라서 원 데이터의 분포를 가능한 유지하면서 데이터의 차원을 줄이는 것이 필요하다. 이를 dimensionality reduction라 한다.

물론 필요한 일부 변수의 데이터만 뽑아서 사용할 수 있지만 (feature selection), 변수들 사이에 어떤 밀접한 관계가 있는지는 미리 알 수가 없어서 이 경우 원데이터의 분포를 잘 반영한다고 볼 수는 없다.

용도

• 경향성 파악
• 복잡한 feature을 단순화하여 pca를 새로운 feature에 사용
• insight 얻기(feature간 correlation check, 비례관계....)
• feature reduction 할때 사용

ex)
iris 데이터로 예를 들면

1. 꽃받침 길이랑 꽃받침 폭 feature들을 pca해서 꽃받침 길이가 커지면 꽃받침 폭도 커지는 경향성파악
2. pca한녀석으로 feature 2개를 대체해서 feature reduction

cf)

• '꽃받침의 길이'와 '꽃받침 폭'은 '꽃의 크기'라는 근본적인 데이터가 두개의 다른 형태로 표현된것에 지나지 않다. 이렇게 바로 측정되지는 않지만 측정된 데이터의 기반에 깔려 안보이는 데이터를 잠재변수(latent variable)라고 한다.

수학적 모델에 대해서 심도 있는 이해를 위해서는 선형대수학을 좀더 공부해와야겠다.

예시까지 적용하며 참고하고 싶다면 링크 참고: http://matrix.skku.ac.kr/math4ai-intro/W12/

틀린 내용이 있다면 댓글 달아주십쇼

1. pca사진: http://matrix.skku.ac.kr/math4ai-intro/W12/
2. 내용 참조:http://matrix.skku.ac.kr/math4ai-intro/W12/
   (예시까지 잘 나와있어서 링크 참고하기)