
베이즈 정리 (Bayes' Theorem)란?
베이즈 정리는 사건이 발생한 후에 원인을 추론하는 데 사용하는 확률 법칙입니다.
즉, 이미 발생한 사건을 바탕으로 다른 사건이 일어날 확률을 업데이트하는 방법을 제공합니다.
1. 베이즈 정리의 공식
베이즈 정리는 조건부 확률을 이용하여 다음과 같이 표현됩니다:
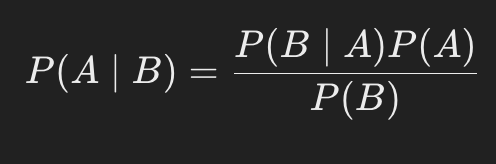
- P(A | B): B가 발생한 후 A가 발생했을 확률 (사후 확률, Posterior Probability)
- P(B | A): A가 발생한 경우 B가 발생할 확률 (우도, Likelihood)
- P(A): A가 발생할 확률 (사전 확률, Prior Probability)
- P(B): B가 발생할 확률 (모든 가능한 경우에서 B가 발생할 확률)
2. 베이즈 정리가 왜 중요한가?
베이즈 정리는 새로운 정보가 주어졌을 때 확률을 업데이트하는 과정입니다.
즉, 기존 확률(사전 확률)을 새로운 정보(우도)를 통해 수정하여 사후 확률을 계산합니다.
- 의학적 진단: 질병이 있을 확률을 검사 결과를 기반으로 업데이트
- 기계 학습: 새로운 데이터가 주어질 때 모델이 확률을 업데이트하는 과정
- 범죄 수사: 주어진 증거를 바탕으로 용의자가 범인일 확률 계산
3. 예제: 질병 진단
어떤 병(예: 독감)에 걸릴 확률이 1%라고 가정하겠습니다.
이 병을 진단하는 검사에서 양성(positive)이 나올 확률은 다음과 같습니다:
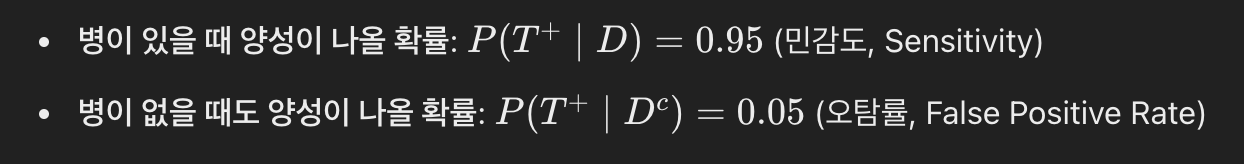
여기서:

우리는 "검사 결과가 양성일 때 실제로 병에 걸렸을 확률" P(D | T^+)을 구해야 합니다.
베이즈 정리 적용
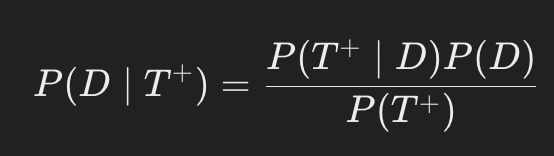
먼저, P(T^+)를 구해야 합니다. 전체적으로 검사에서 양성이 나올 확률은 다음과 같이 계산됩니다:
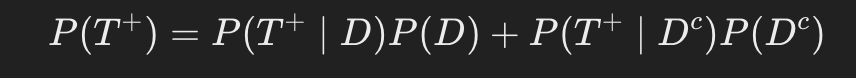
대입하면:
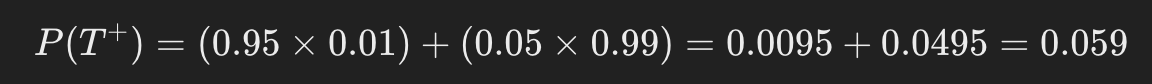
이제, 베이즈 정리를 사용하여 P(D | T^+)을 구합니다:
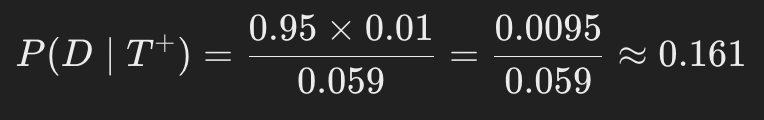
즉, 검사에서 양성이 나왔다고 해서 실제로 병에 걸렸을 확률은 약 16.1%입니다.
(검사 결과만 믿으면 안 되는 이유!)
4. 확장: 여러 개의 원인 (전확률 정리 활용)
베이즈 정리는 하나의 원인(A)이 아니라 여러 원인들이 있을 때도 사용됩니다.
만약 B가 여러 개의 가능한 원인 A_1, A_2, ..., A_n 중 하나로 인해 발생했다면:
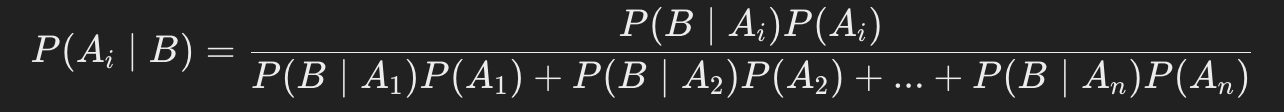
이것을 전확률 정리 (Law of Total Probability)라고 합니다.
5. 결론
-
베이즈 정리는 새로운 정보가 주어졌을 때 확률을 업데이트하는 방법입니다.
-
조건부 확률을 활용하여 원인을 추론할 수 있습니다.
-
의학, 인공지능, 금융, 범죄 수사 등에서 널리 사용됩니다.
-
기본 공식:
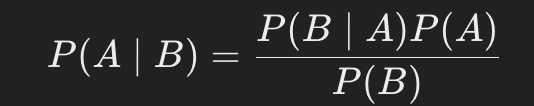
-
응용 예제: 검사 결과가 양성일 때 실제 질병 확률을 구하는 문제
혹시 더 궁금한 점 있으면 질문해주세요! 😊
