파이썬 머신러닝 완벽 가이드 - 7. Dimension Reduction(1) (PCA, LDA)

Mios·2022년 10월 11일

AI AI study Dimension Reduction LDA PCA mechinelearning python 머신러닝 차원 축소 파머완 파이썬

[AI Study] 파이썬 머신러닝 완벽 가이드

목록 보기

10/14

Dimension Reduction 차원 축소

: 매우 많은 피처로 구성된 다차원 세트의 차원을 축소해 새로운 차원의 데이터 세트를 생성하는 것

다차원 데이터 세트의 문제점
1. 차원이 증가할 수록 데이터 포인트 간의 거리가 기하급수적으로 멀어지고, 희소한Sparse 구조를 가져 예측 신뢰도가 떨어진다.
2. 다중공선성 문제(독립변수 간의 상관관계가 높은 것)로 예측 성능 저하
  - 회귀분석의 전제 가정 위배 : 독립변수간 상관관계는 높으면 안된다
차원 축소의 분류
- 피처(특성) 선택 : 특정 피처에 종속성이 강한 불필요 피처는 아예 제거 + 데이터 특징 잘 나타내는 주요 피처만 선택
- 피처(특성) 추출 : 기촌 피처를 저차원의 중요 피처로 압축하여 추출 ⇒ 기존 피처와 완전히 다른 새로운 값이 됨
  - 단순 압축이 아닌, 피처를 합축적으로 더 잘 설명할 수 있는 또 다른 공간으로 매칭하여 추출하는 것
    ex) 학생의 모의고사성적, 내신성적, 수능성적, 봉사활동, 대외활동, 수상경력 등 ⇒ 학업 성취도, 커뮤니케이션 능력, 문제해결력 등 더 함축적인 요약 특성으로 추출할 수 있음
  - 가장 중요한 의미 : 데이터를 더 잘 설명할 수 있음 잠재적인 요소 추출 PCA, SVD, NMF 등
차원 축소의 활용
1. 이미지 데이터에서 잠재된 특성을 피처로 도출해 함축적 형태의 이미지 변환과 압축 수행 ⇒ 원본보다 작은 차원으로 과적향 방지
2. 텍스트 문서의 숨겨진 의미 추출. 문서 내 단어들의 구성에서 숨겨져 있는 시맨틱Semantic 의미나 토픽topic을 잠재 요소로 간주하고 이를 찾아낸다.

1. PCA(Principal Component Analysis, 주성분 분석)

: 변수 간 상관관계를 이용해 이를 대표하는 주성분을 추출해 차원을 축소하는 방법

PCA의 주성분: 정보 유실을 최소화하기 위해 가장 높은 분산을 가지는 데이터를 찾아, 이 축으로 차원을 축소한다. 즉, 분산이 데이터의 특성을 가장 잘 나타내는 것으로 간주한다.
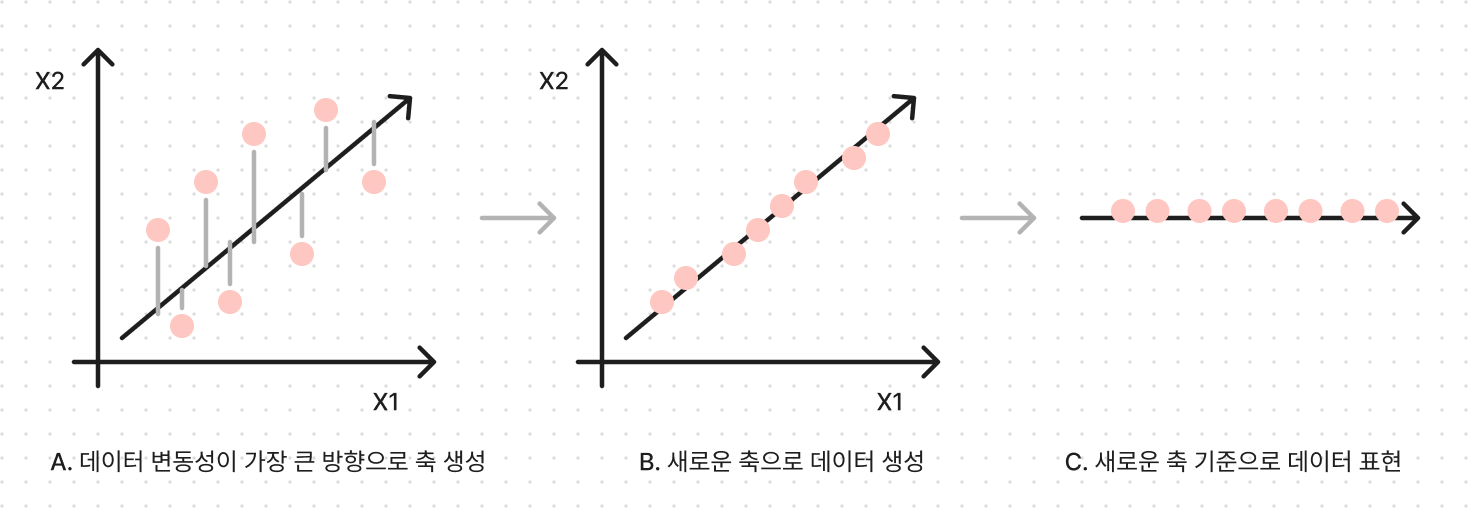
PCA 차원 축소 하는 방법

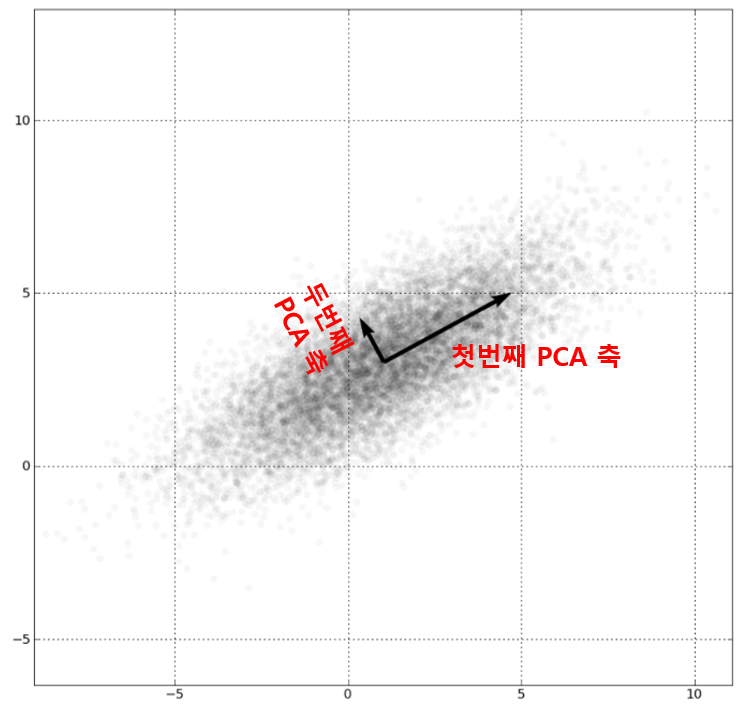
첫 번째 벡터 축 : 가장 큰 데이터 변동성(Variance)을 기반으로 생성
두 번째 벡터 축 : 첫 번째 벡터 축에 직각이 되는 벡터(직교 벡터)를 축으로 함
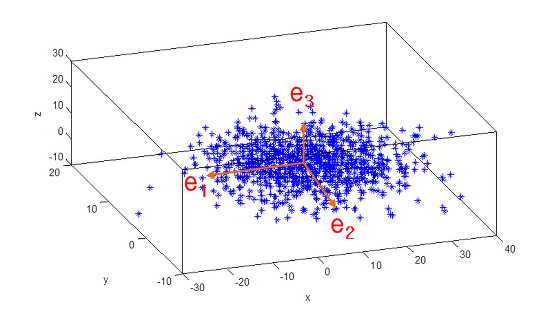
세 번째 벡터 축 : 다시 두 번째 축과 직각이 되는 벡터를 설정하는 방식으로 축 생성
- 선형대수 관점 : 입력 데이터의 공분산 행렬(Covariance Matrix)을 고유값 분해하고, 이렇게 구한 고유벡터에 입력 데이터를 선형 변환하는 것
PCA의 주성분 : 위에서 말하는 고유벡터. 입력 데이터의 분산이 가장 큰 방향을 나타낸다.
고유값(eigenvalue) : 고유벡터의 크기. 입력 데이터의 분산을 나타냄
선형 변환 : 특정 벡터에 행렬 A를 곱해 새로운 벡터로 변환하는 것, 특정 벡터를 하나의 공간(행렬을 공간으로 가정)에서 다른 공간으로 투영하는 개념
고유 벡터 : 행렬A를 곱하더라도 방향이 변하지 않고, 그 크기만 변하는 벡터
- Ax = ax (A: 행렬, x: 고유 벡터, a: 스칼라 값)
- 이 고유 벡터는 여러 개가 존재하며,
- 정방 행렬은 최대 그 차원 수 만큼 고유 벡터를 가질 수 있다. (예: 2x2 행렬은 최대 2개의 고유벡터를 가질 수 있음, 3x3은 3개)
- 이렇듯 고유벡터는 행렬이 작용하는 힘의 방향과 관계가 있어서, 행렬을 분해하는데 사용됨
분산 : 한 개의 특정한 변수의 데이터 변동을 의미
공분산 : 두 변수 간의 변동을 의미
- 사람의 키 변수를 X, 몸무게 변수를 Y로 둘 때, 공분산 $Cov(X,Y) > 0$ == X(키)가 증가할 때 Y(몸무게)도 증가한다는 의미
공분산 행렬 : 여러 변수와 관련된 공분산을 포함하는, 정방 행렬 & 대칭 행렬

X Y Z
X 3.0 -0.71 -0.24
Y -0.71 4.5 0.28
Z -0.24 0.28 0.91
- 대각선 원소는 각 변수(X, Y, Z)의 분산을 의미
- 대각선 외의 원소는, 가능한 모든 변수 쌍 간의 공분산을 의미
- X와 Y의 공분산 = -0.71
정방 행렬(Diagonal Matrix) : 열과 행이 같은 행렬
대칭 행렬(Symmetric Matrix) : 정방 행렬 중에서 대각 원소를 중심으로 원소값이 대칭되는 행렬, $A^T = A$ 대
- 대칭 행렬은 항상 고유 벡터를 직교 행렬로, 고유값을 정방 행렬로 대각화 할 수 있음 ⇒ 고유값 분해
공분산 행렬의 분해
- $C = P \sum P^T$
  
  $C = [e_1\cdots e_n] \begin{bmatrix} \lambda_1 \> \cdots\> 0 \\ \cdots \> \cdots \> \cdots \\ 0 \> \cdots \> \lambda_n \end{bmatrix} \begin{bmatrix} e_1^t \\ \cdots \\ e_n^t \end{bmatrix}$
  
  $C$ = 고유벡터의 직교 행렬 고유값 정방행렬 고유벡터 직교행렬의 전치 행렬
  - $e_i$ 는 $i$ 번째 고유 벡터
  - $\lambda_i$ 는 $i$ 번째 고유벡터의 크기(고유값)
  - $e_1$ 는 가장 분산이 큰 방향을 가진 고유 벡터
  - $e_2$ 는 $e_1$ 에 수직이면서, 그 다음으로 분산이 큰 방향을 가진 고유벡터
PCA : 입력 데이터의 공분산 행렬이 고유벡터와 고유값으로 분해될 수 있으며, 이렇게 분해된 고유벡터를 이용해 입력 데이터를 선형 변환하는 방식
수행
1. 입력 데이터 세트의 공분산 행렬 생성 ( $C$ )
2. 공분산 행렬의 고유벡터( $e_i$ )와 고유값( $\lambda_i$ )을 계산
3. 고유값( $\lambda_i$ )이 가장 큰 순으로 K개(PCA 변환 차수)만큼 고유벡터( $e_i$ )를 추출
4. 고유값( $\lambda_i$ )이 가장 큰 순으로 추출된 고유벡터( $e_i$ )를 이용해 새롭게 입력 데이터 변환

	X	Y	Z
X	3.0	-0.71	-0.24
Y	-0.71	4.5	0.28
Z	-0.24	0.28	0.91

📐 PCA의 구성 개념 정리

PCA : 입력 데이터의 공분산 행렬(Covariance Matrix)을 고유값 분해하고, 이렇게 구한 고유벡터(주성분)에 입력 데이터를 선형 변환하는 것
- 주성분 : 위에서 말하는 고유벡터. 입력 데이터의 분산이 가장 큰 방향을 나타낸다.
- 공분산 (행렬) : 두 변수 간의 변동을 의미 (여러 변수와 관련된 공분산을 포함하는 대칭 행렬)
- 공분산 행렬은 항상 고유 벡터를 직교 행렬로, 고유값을 정방 행렬로 대각화 할 수 있음 ⇒ 고유값 분해
- 고유값 ( $\lambda$ ) : 고유벡터의 크기, 입력 데이터의 분산을 나타냄
- 고유 벡터 ( $e$ ) : 행렬A 곱해도, 방향 변화 X & 크기만 변화 O 벡터, 행렬이 작용하는 힘의 방향과 관계 있음
- 선형 변환 : 특정 벡터(고유 벡터)에 행렬 A(입력 데이터)를 곱해 새로운 벡터로 변환하는 것
  - 특정 벡터를 하나의 공간(행렬을 공간으로 가정)에서 다른 공간으로 투영하는 개념
공분산 행렬의 분해
- $C = [e_1\cdots e_n] \begin{bmatrix} \lambda_1 \> \cdots\> 0 \\ \cdots \> \cdots \> \cdots \\ 0 \> \cdots \> \lambda_n \end{bmatrix} \begin{bmatrix} e_1^t \\ \cdots \\ e_n^t \end{bmatrix}$
  
  $[e_1\cdots e_n]$ = 고유 벡터 : 행렬이 작용하는 힘의 방향
  
  $\begin{bmatrix} \lambda_1 \> \cdots\> 0 \\ \cdots \> \cdots \> \cdots \\ 0 \> \cdots \> \lambda_n \end{bmatrix}$ = 고유값 : 입력데이터의 분산 & 고유 벡터의 크기
- $e_1$ 는 가장 분산이 큰 방향을 가진 고유 벡터, $e_2$ 는 $e_1$ 에 수직이면서, 그 다음으로 분산이 큰 방향을 가진 고유벡터

PCA를 적용하기 위해서는 각 속성값을 동일한 스케일로 변환해야 한다. ⇒ StandardScaler
- 여러 속성 값을 연상해야 하므로, 속성의 스케일에 영향을 받기 때문

사용


from sklearn.preprocessing import StandardScaler

# Target 값을 제외한 모든 속성 값을 StandardScaler를 이용하여 표준 정규 분포를 가지는 값들로 변환
iris_scaled = StandardScaler().fit_transform(irisDF.iloc[:, :-1])

from sklearn.decomposition import PCA

pca = PCA(n_components=2)

#fit( )과 transform( ) 을 호출하여 PCA 변환 데이터 반환
pca.fit(iris_scaled)
iris_pca = pca.transform(iris_scaled)
print(iris_pca.shape)

# PCA 환된 데이터의 컬럼명을 각각 pca_component_1, pca_component_2로 명명
pca_columns=['pca_component_1','pca_component_2']
irisDF_pca = pd.DataFrame(iris_pca, columns=pca_columns)
irisDF_pca['target']=iris.target
irisDF_pca.head(3)

n_components: PCA로 변환할 차원의 수
이후 fit()과 transform()을 호출해 PCA 변환 데이터 반환

explainedvariance_ratio: 전체 변동성에서 개별 PCA 컴포넌트별로 차지하는 변동성 비율 제공

pca.explained_variance_ratio_

> [0.72962445 0.22850762]
>> 원본 데이터의 0.95 변동성을 설명할 수 있음

신용카드 고객 데이터

df.corr()로 각 속상간의 상관도를 구한 뒤, heatmap으로 보기
상관도 높은거 묶어서 하기(?)

2. LDA(Linear Discriminant Analysis, 선형 판별 분석)

: PCA와 유사하지만, 지도 학습의 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원 축소

PCA는 입력 데이터의 변동성의 가장 큰 축을 찾았지만, LDA는 입력 데이터의 결정 값 클래스를 초대한 분리할 수 있는 축을 찾음
입력 데이터의 결정값 클래스를 최대한으로 분리할 수 있는 축을 찾기 위해, 클래스 간 분산(between)과 클래스 내부 분산(within)의 비율을 최대화하는 방식으로 차원 축소
- 클래스 간 분산은 크게, 클래스 내부 분산은 작게
$S_W^TS_B = [e_1\cdots e_n] \begin{bmatrix} \lambda_1 \> \cdots\> 0 \\ \cdots \> \cdots \> \cdots \\ 0 \> \cdots \> \lambda_n \end{bmatrix} \begin{bmatrix} e_1^T \\ \cdots \\ e_n^T \end{bmatrix}$

$[e_1\cdots e_n]$ = 고유 벡터 : 행렬이 작용하는 힘의 방향

$\begin{bmatrix} \lambda_1 \> \cdots\> 0 \\ \cdots \> \cdots \> \cdots \\ 0 \> \cdots \> \lambda_n \end{bmatrix}$ = 고유값 : 입력데이터의 분산 & 고유 벡터의 크기

수행
1. 입력 데이터의 결정값 클래스 별로 개별 피처의 평균 벡터(mean vector)를 기반으로 [클래스 내부, 클래스 간 분산 행렬]을 구한다.
2. 클래스 내부 분산 행렬( $S_W$ ), 클래스 간 분산 행렬( $S_B$ ) ⇒ 두 행렬을 고유벡터( $e$ )로 분해
3. 고유값이 가장 큰 순으로 K개(LDA 변환 차수)만큼 추출
4. 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력 데이터를 변환

사용

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris

iris = load_iris()
iris_scaled = StandardScaler().fit_transform(iris.data)

lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(iris_scaled, iris.target) # 지도학습이라, fit할 때, 클래스 결정값 (y) 넣어야함
iris_lda = lda.transform(iris_scaled)
print(iris_lda.shape)

LDA는 실제로는 PCA와 다르게 비지도학습이 아닌 지도학습 ⇒ 즉, 클래스 결정값이 변환시에 필요함.

Mios

mios의 데이터 놀이터 | Instagram@data.decision (하단 홈 아이콘 버튼)

이전 포스트

파이썬 머신러닝 완벽 가이드 - 6. Regression(2) (규제, 로지스틱회귀, 회귀 트리 및 예제)

다음 포스트