5. 규제 Regularization

1. 릿지 회귀 Ridge

: $w^2$에 대해 패널티를 부여하는 방식. 주요 생성 파라미터는 alpha로, alpha가 커질 수록 회귀 계수 값을 작게 만든다.

• $RSS(w) + alpha*||w||_2^2$ 식을 최소화하는 w를 찾는 것

from sklearn.linear_model import Ridge

2. 라쏘 회귀 Lasso

: $|w|$에 패널티를 부여하는 방식. 불필요한 회귀 계수를 급격하게 감소시켜 0으로 만든다.

• $RSS(w) + alpha*||w||_1$ 식을 최소화하는 w를 찾는 것

from sklearn.linear_model import Lasso

3. 엘라스틱넷 회귀 ElasticNet

• L2규제와 L1규제를 결합한 회귀
  • L1 라쏘 회귀가 중요 피처만 셀렉션하고 다른 피처들은 회귀 계수를 0으로 만드는 성향이 강함
  • alpha 값에 따라 회귀 계수 값이 급격히 변동할 수 있는데, 이를 완화하기 위해 L2 릿지를 L1 라쏘 회귀에 추가한 것
  • 반대로 엘라스틱넷 회귀의 단점은 L1 + L2로 수행시간이 상대적으로 오래 걸린다는 것
• $RSS(w) + alpha1*||w||_1+alpha2*||w||_2^2$ 식을 최소화하는 w를 찾는 것
  • 엘라스틱 규제 : $a * L1 + b * L2$
  • 릿지와 라쏘의 alpha값과는 다름
  • $a$ = L1 규제의 alpha값, $b$ = L2 규제의 alpha값
  • 엘라스틱넷 회귀의 alpha값은 = $a+b$
• 주요 생성 파라미터
  • alpha = $a + b$
  • l1_ratio = $\frac{a}{a+b}$
    • l1_ratio = 0이면, a=0이므로 L2규제와 동일
    • l1_ratio = 1이면, b=0이므로 L1 규제와 동일

from sklearn.linear_model import ElasticNet

4. 선형 회귀 모델을 위한 데이터 변환

• 데이터 분포도의 정규화와 인코딩의 중요성
• 데이터 변환 : 선형 회귀 모델은 피처값과 타겟값의 분포가 정규분포로 된 형태를 선호
  • 정규분포 형태가 아니라, 특정값 분포로 치우친 왜곡(Skew)된 형태의 분포도일 경우, 성능에 부정적 영향 줄 가능성 높음

  1. StandardScaler : 평균이 0, 분산이 1인 정규분포를 가진 데이터 세트로 변환

     MinMaxScaler : 최소값이 0, 최대값이 1인 값으로 정규화 수행

  2. 스케일링/정규화를 수행한 데이터 세트에 다시 다항 특성을 적용하여 변환

     • 1번 방법을 통해 성능 향상이 없는 경우, 2번을 적용하는 경우가 많음

  3. ⭐️로그 변환⭐️ : log함수를 적용하여 정규분포에 가까운 형태로 변환

     • 이 방법을 주로 사용
       • 1번은 성능 향상을 크게 기대하기 어려우며
       • 2번은 피처 갯수가 매우 많을 경우에는 다항 변환으로 생기는 피처 갯수가 기하급수로 늘어나서 과적합 이슈 발생 높음
     • 타깃값의 경우는 일반적으로 로그 변환을 적용
       → 타깃값을 다른류의 정규값으로 변환하면 원복이 어렵고, 왜곡된 타깃 분포도를 로그 변환하면 성능 향상된 경우가 많은 사례에서 검증됐음
     • np.log1p() = $1 + log()$ 사용
       • $log()$는 언더플로우 발생 가능성이 있기 때문

6. 로지스틱 회귀 Logistic Regression

: 선형 회귀 방식을 분류에 적용한 알고리즘 (이진 분류에 뛰어남)

: 시그모이드Sigmoid 함수 최적선을 찾고 이 시그모이드 함수의 반환값을 확률로 간주해 확률에 따라 분류를 결정한다.

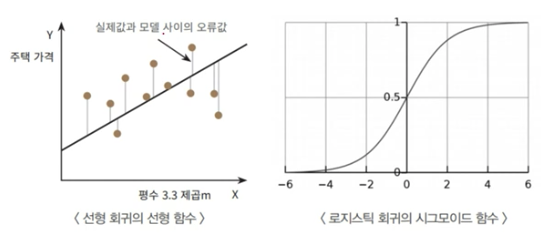
• 시그모이드 함수 : $y = \frac{1}{1+e^{-x}}$
  • $x$ → $\infty$ : $y=1$
  • $x$ → $-\infty$ : $y=0$
  • $x$ → $0$ : $y=0.5$
• 로지스틱 회귀 하이퍼 파라미터
  • penalty : 규제 유형 설정. ‘l2’, ‘l1’ (기본은 l2)
  • C : 규제 강도 조절하는 alpha의 역수 (1/alpha) $\therefore$ 작을수록 규제강도 높아짐

7. 회귀 트리

: 회귀를 위한 트리를 생성하고 이를 기반으로 회귀 예측 진행

: 리프 노드에 속한 데이터 값의 평균값으로 회귀 예측값을 계산

: 결정트리, 랜덤포레스트, GBM, LightGBM, XGBoost 등 모든 트리 기반 알고리즘은 회귀 계산 가능

(뒤에 Regressor. 예: DecisionTreeRegressor)

단, 선형 회귀와 다른 처리 방식이므로 회귀 계수를 제공하는 coef 속성은 없다. 대신 피처별 중요도를 알려주는 feature_importances 제공

8. 회귀 실습

8.1. 캐글 자전거 대여 수요예측

• 회귀 모델 전, 데이터 전처리시 주의점
  • 결괏값이 정규 분포로 돼 있는지 확인
  • 카테고리형 회귀 모델의 경우 → 원-핫 인코딩으로 피처를 인코딩 하는 것
• 예측 오류가 큰 경우 ⇒ Target 값의 분포가 왜곡된 형태를 이루고 있는지 확인하기

  def get_top_error_data(y_test, pred, n_tops = 5):
      # DataFrame에 컬럼들로 실제 대여횟수(count)와 예측 값을 서로 비교 할 수 있도록 생성. 
      result_df = pd.DataFrame(y_test.values, columns=['real_count'])
      result_df['predicted_count']= np.round(pred)
      result_df['diff'] = np.abs(result_df['real_count'] - result_df['predicted_count'])
      # 예측값과 실제값이 가장 큰 데이터 순으로 출력. 
      print(result_df.sort_values('diff', ascending=False)[:n_tops])
      
  get_top_error_data(y_test,pred,n_tops=5)
  
  y_target.hist()
  
  y_log_transform = np.log1p(y_target)
  y_log_transform.hist()

  • 결괏값이 왜곡된 경우, 로그 변환 하면 좋다

    y_log_transform = np.log1p(y_target)
    y_log_transform.hist()

  • 로그 변환된 것 → 원상 복구 : np.expm1(y_data)

    # 타겟 컬럼인 count 값을 log1p 로 Log 변환
    y_target_log = np.log1p(y_target)
    
    # 로그 변환된 y_target_log를 반영하여 학습/테스트 데이터 셋 분할
    X_train, X_test, y_train, y_test = train_test_split(X_features, y_target_log, test_size=0.3, random_state=0)
    lr_reg = LinearRegression()
    lr_reg.fit(X_train, y_train)
    pred = lr_reg.predict(X_test)
    
    # 테스트 데이터 셋의 Target 값은 Log 변환되었으므로 다시 expm1를 이용하여 원래 scale로 변환
    y_test_exp = np.expm1(y_test)
    
    # 예측 값 역시 Log 변환된 타겟 기반으로 학습되어 예측되었으므로 다시 exmpl으로 scale변환
    pred_exp = np.expm1(pred)
    
    evaluate_regr(y_test_exp ,pred_exp)

• 숫자로 되어 있지만, 카테고리형이어야 할 feature ⇒ one-hot 인코딩

  # 'year', month', 'day', hour'등의 피처들을 One Hot Encoding
  X_features_ohe = pd.get_dummies(X_features, columns=['year', 'month','day', 'hour', 'holiday',
                                                'workingday','season','weather'])
                                  # X_features에서, columns=[] 들의 col을 o-h 인코딩 하겠다.
  
  X_features_ohe.head()

8.2. 캐글 주택 가격 : 고급 회귀 기법

9. 정리

• 기본 개념: 경사하강법 Gradient Descent
• 평가: MAE, MSE, RMSE, R^2
• Linear Regressor
  • 단항 회귀
  • 다항 회귀
• Reaularization
  • Ridge
  • Lasso
  • ElasticNet
• Logistic Regression
• Regression Tree

+데이터 스케일링/정규화, 인코딩

+스태킹 기법 가능