1. Introduction

첫 장은 소개이므로, 간단히 요약 정리하는 수준으로 적어볼 예정입니다.

1. 개념

Optimization(최적화)를 하기 위해서는 먼저 Objective(목적)를 정의해야 됩니다. 이 용어는 Cost(비용), Energy와 같은 단어로 표현됩니다. 저는 개인적으로 Cost를 많이 사용하지만, Objective가 좀 더 일반적인 용어입니다.

이 Objective를 정의하는 Function(함수)을 동일하게 Objective Function, Cost Function, Energy Function이라고 합니다. Function은 당연히 입력과 출력이 존재합니다. 입력을 여기에서는 variable이라고 하며, parameter 또는 unknown이라고 부르기도 합니다. 최적화는 우리가 원하는 최적의 Objective(목적, 비용, Energy 무엇이든..)가 나오게 만드는 입력 값, variable을 찾는 작업을 말합니다. 여기서 최적이라고 하면, 보통은 최소 또는 최대를 말합니다. 이렇게 variable과 objective, 그리고 그 관계를 의미하는 objective function을 합쳐서 model이라고 부립니다. 사실 model은 최적화를 위한 용어가 아니라, 입출력이 있는 시스템을 모두 model이라고 부릅니다. model에는 environment condition(환경 조건)이 추가될 수 있습니다. 최적화에서는 이를 constraint(구속)이라고 많이 지칭합니다. constraint는 말 그대로 variable에 구속 조건을 추가하는 것입니다. 최적화를 할 때, 구속 조건 내에서 variable이 결정되어야 한다는 말입니다.

그림으로 표현하면 아래 그림과 같습니다.

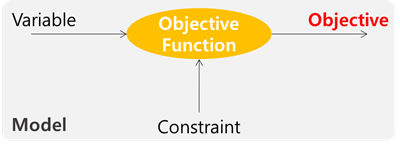
이를 수학적으로 표현하면 아래 수식과 같습니다.

$\underset{x\in R^n}{\min} f(x) \quad \text{subject to} \begin{cases} c_i(x)=0, \quad i \in \mathcal E \\ c_i(x)\geq 0, \quad i \in \mathcal I\end{cases}$

조금 생소할 수 있는 기호가 나옵니다. $i \in \mathcal E$, $i \in \mathcal I$ 입니다. $i \in \mathcal E$는 이 constraint가 equality라는 의미입니다. variable이 어떤 라인이나 면을 따라 움직인다는 말입니다. 반대로 $i \in \mathcal I$는 inequality 입니다. 등호가 붙어 있어 이 경우는 variable이 공간 상에 위치한다는 의미이며, 훨씬 어려운 문제가 됩니다.

2. 예제

책에서는 아래와 같은 예제를 보여줍니다.

$\text{min }(x_1-2)^2+(x_2-1)^2 \quad \text{subject to} \begin{cases} x_1^2-x_2\leq 0 \\ x_1+x_2\leq 2 \end{cases}$

이 예제에서 Objective Function은 $(x_1-2)^2+(x_2-1)^2$, $(2,1)$을 중심으로하는 원의 방정식입니다. 이 Function만 본다면, 최소의 조건은 $x_1=2, x_2=1$인 경우이다. 하지만 여기에 inequality constraint가 추가되었습니다. $x_1, x_2$는 아래의 그림에서 회색 영역에만 있어야 된다는 조건입니다. 사실 이 문제는 간단한 수학문제로 최적값($x_*$)은 $x_1=1, x_2=1$이 됩니다.

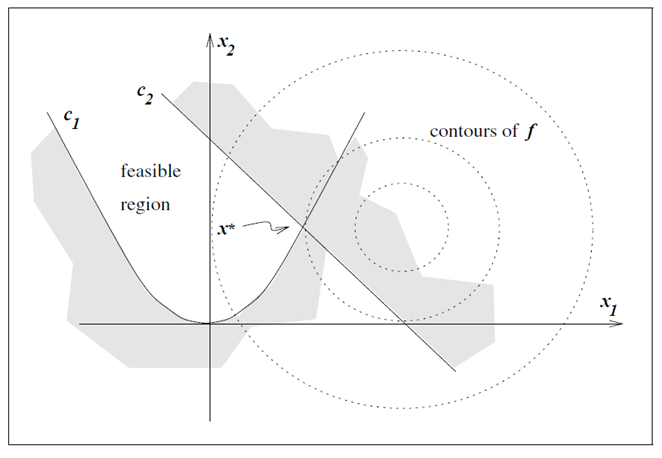
수학적으로 풀면 매우 간단히 풀리는 문제이지만, 만약 이를 코딩으로 한다면 어떨까요?

Brute하게 말그대로 무식하게 한번 코드를 만들면 아래와 같이 될겁니다.

x1과 x2를 -100 ~ 100까지 순회하며, object를 계산한 다음, 구속조건을 만족할 경우에만 업데이트를 하여 최소가 되는 $x_1, x_2$을 찾는 코드입니다. 어디 코딩 테스트에 제출하면 떨어지기 딱 좋은 코드입니다.

그런데 엄밀히 따져보면, 코딩 테스트에서 나올만한 내용이 아니라, 현업에서 마주한 수학적인 문제라면 대부분 이런 식으로 접근할 수 밖에 없습니다. 기껏해봐야 순회를 줄이기 위한 테크닉을 쓰거나, 병렬 처리를 하든지 할겁니다. 하지만 문제가 더 복잡해지고, 정밀도가 높아져야 한다면 이런 방식은 불가능하다는 것을 금방 깨닫게 됩니다. 그래서 optimization이론을 공부할 필요가 있습니다.

class BruteOptimize
{
public: 
	static bool optimize(double &optX1, double &optX2)
	{
		double infinite = 1e+20;

		optX1 = infinite;
		optX2 = infinite;

		double minObject = infinite;
		for (int x1 = -100; x1 < 100; ++x1)
		{
			for (int x2 = -100; x2 < 100; ++x2)
			{
				double object = (x1 - 2.0) * (x1 - 2.0) + (x2 - 1.0) * (x2 - 1.0);

				if (x1 * x1 - x2 <= 0 && x1 + x2 <= 2.0)
				{
					if (object < minObject)
					{
						minObject = object;
						optX1 = x1;
						optX2 = x2;
					}
				}
			}
		}

		if (optX1 == infinite || optX2 == infinite)
			return false;

		return true;
	}
};

3. 기타 개념 소개

LINEAR PROGRAMMING

아래 수식과 같이, objective function과 기타 constraint가 linear(선형)인 경우를 말합니다.

$\min \displaystyle\sum_{ij} c_{ij}x_{ij}$

$\displaystyle\sum_{i=0}^2 x_{ij} \leq a_i$, $i=1, 2$

CONTINUOUS VERSUS DISCRETE OPTIMIZATION

우리가 다루는 최적화 문제중에서는 연속적(Continuous)이지 않은 데이터가 있을 수 있습니다. 예를 들어, 농장에 트랙터를 몇 대 투입해야 최적일까요 이런 문제가 있다면, 연속적인 숫자로 만들어진 결과는 "3.4대를 투입하셔요" 가 될 수 있습니다. 누가봐도 틀린 말입니다. 그럼 이 경우에 3대는 부족하니 4대면 남지만, 충분하니 4대를 투입하자 이런 결론을 낼 수도 있습니다. 이것도 좋은 방법이겠지만, 이 책에서는 그렇게 하지 말고, 정석적인 Discrete(이산) Optimization 기법을 사용하라고 되어 있습니다.
Discrete Optimization은 데이터를 integer형태로 다룹니다. 개발자에게는 매우 익숙한 용어죠. 즉 정수로만 최적화를 수행한다는 의미입니다.

$x_{ij} \in Z\quad \text{for all i, j}$

어떤 문제에서는 연속적인 실수형 데이터와 정수형 데이터가 섞여 있을 수 있습니다. 이 경우에는 Mixed Integer Programming이라는 기법을 사용해야 합니다. 이 책에서는 사실 이 부분은 다루지 않고, 참고할 수 있는 논문이나 저서등을 소개하고 끝내고 있습니다.
저도 오래 전에 비슷한 문제를 다뤄본 경험이 있어, 후에 별도로 내용을 정리할 예정입니다.

CONSTRAINED AND UNCONSTRAINED OPTIMIZATION

앞서 한번 언급된 용어입니다. Constraint가 없다면 unconstrained optimization, 있다면 constrainted optimization입니다. constrainted optimization은 많은 경우에, 선형적으로 최적화를 할 수 없기 때문에, 이 경우를 Nonlinear programming이라고 합니다. Nonlinear programming은 대부분의 경우 특별한 테크닉을 요구합니다.

GLOBAL AND LOCAL OPTIMIZATION

최적화를 하면서 가장 많이 마주치게 될 문제가 바로 최적화의 결과가 Local Optimum이나 Global Optimum이냐 입니다. 당연히 Global Optimum이 모든 경우에 대한 해답이기 때문에 좋지만, 상당히 어려운 문제입니다. 이 책에서 다룰 기법들 역시 Local Optimum을 찾는 경우입니다.

아래 그림과 같이, 특정 초기값을 가지고 시작하는 최적화의 경우, 초기 값의 상태에 따라서 결과가 달라질 수가 있고, 이는 local minimum에 빠지게 합니다.

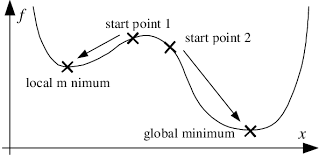
STOCHASTIC AND DETERMINISTIC OPTIMIZATION

최근에 주목을 많이 받는 최적화 기법중에 하나가 확률(Probability)적인 접근으로 다루는 Stochastic Optimization입니다. 여기서는 variable이 확률이 됩니다. 최적화를 수행하고자 하는 대상을 대표하는 값(variable)이 특정한 숫자로 떨어지지 않는 경우 즉, Deterministic이 아닌 경우에 사용합니다. 이 책에서는 Stochastic Optimization은 다루지 않지만, 이 자체가 하나의 분야로 자리 잡았기 때문에, 별도로 다루도록 하겠습니다.

OPTIMIZATION ALGORITHMS

최적화를 수행할 때, 중요한 3가지 요소를 책에서 언급하고 있습니다.
Robustness(강인성), Efficiency(효율성), Accuracy(정확성) 입니다.
강인성은 최적화 알고리즘이 외부 조건에 의해 결과가 달라지지 않고 꾸준히 결과를 도출할 수 있어야 된다는 의미입니다. 튜닝 파라미터를 조금만 달리하면 결과가 확 바껴버리는 경우가 종종 발생하는데, 강인성이 부족한 경우라고 할 수 있습니다.
효율성은 최적화 알고리즘을 수행하는데 있어, 자원을 아껴써라는 의미입니다. 즉 제가 예시로 작성한 위의 코드와 같이 Brute한 방식은 사용하지 말라는 말입니다. (하지만, PC가 엄청 좋다면...... 병렬화도 쉽다면......데이터도 적당히 작다면..... 그냥 Brute하게 하세요..Simple is best 라는 개발자의 의견입니다.)
정확성은 당연한 말입니다. 결과가 정답에 가까워야죠.

CONVEXITY

Convex의 정의를 책에서는 수학적으로 설명하고 있는데, 아래 그림을 보면 쉽게 이해가 됩니다. 좌측 그림과 같이, 공간 내에서 어떠한 두 점을 선택해서 이어도, 공간을 벗어나지 않으면 Convex, 우측처럼 공간을 벗어나는 경우가 있다면, Non-convex입니다.

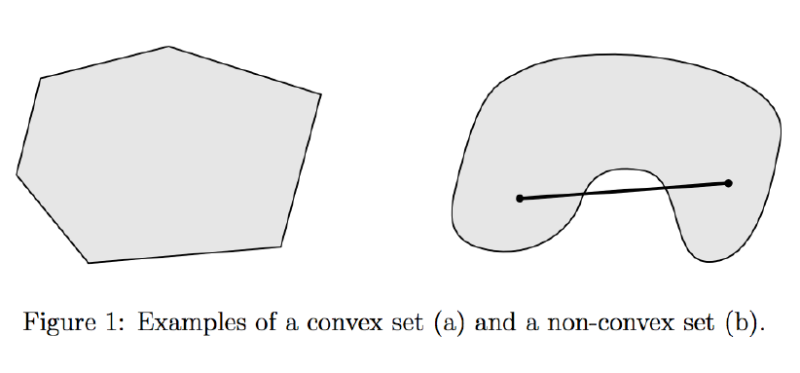
Convex가 중요한 이유는, 앞서 한번 언급한 Global optimization과 관련이 있다. Convex에서는 local minimum이 발생할 수 없기 때문에(Objective Function의 형태가 구불구불 들어가고 나오고해야 local minimum이 발생합니다.), 만약 Objective Function이 convex형태라면, Convex Programming기법을 통해서 Global Optimization을 수행할 수 있다는 의미이기 때문에 중요한 개념입니다.

1장을 마치며..

1장은 기본적인 최적화의 개념과 예시, 종류 등에 대해 설명하고 있습니다.
개인적으로 중요하다고 생각하는 부분은 최적화 이론 자체는 분명 수학적인 영역이지만, Objective를 정의하는 것은 Domain지식이라는 점입니다. 즉 소속된 Domain의 전문가가 최적화도 잘 할 수 있다.
이 말은 최적화에 국한된 것은 아닙니다. 개발자라면 개발 언어, 프레임워크를 잘해야 되지만, 개발하고자 하는 대상의 Domain지식 학습에도 게을리하지 말아야 한다는 뜻도 됩니다. 제가 후배들한테 많이 강조하는 부분이기도 합니다.

위의 내용은 책을 많이 참고하긴 했지만, 직역은 되도록 피했습니다. 책의 컨텐츠 순서는 따르데 되도록이면 제가 알고 있는 내용, 제가 경험해본 내용에 근거하여 설명하도록 노력했습니다. 앞으로도 이렇게 진행할 예정입니다.

고작 1장 소개 끝냈는데, 벌써 힘들어오네요. 끝낼 수 있을지 모르겠습니다.