2. Fundamentals of Unconstrained Optimization

2장 입니다.
2장 역시 간단한 개념 소개를 하기 때문에 간략하게 언급하는 정도로 넘어가겠습니다.
용어 정도 알고 넘어가는 정도면 되겠네요.

1. Solution이란

Solution, 우리 말로는 해를 말합니다.
책에서는 1장에서도 언급된 개념인 Global 과 Local optimization에 의해 Solution이 결정된다고 적혀있습니다.

각 항목별 정의는 다음과 같이 하고 있습니다.

A point $x^*$ is a global minimizer if $f(x^*)\leq f(x)$ for all $x$

A point $x^*$ is a local minimizer if there is a neighborhood $N$ of $x^*$ such that $f(x^*)\leq f(x)$ for all $x$

Global은 모든 x에 대해서 최소인 Solution이며, Local은 인접한 $N$영역의 x에 중에서만 최소인 Solution을 의미합니다.

Local은 다시 strict(strong)와 weak로 구분을 하고 있습니다.

A point $x^*$ is a strict(strong) local minimizer if there is a neighborhood $N$ of $x^*$ such that $f(x^*)\lt f(x)$ for all $x \in N$ with $x \neq x^*$

인접한 $N$영역에서 오직 한개의 해만 존재할 때를 strict(strong)이라고 합니다.
예를 들어, $f(x)=(x-2)^4$라는 objective 함수가 있다면, 해는 2 하나 밖에 없습니다. 이런 경우를 strict라고 합니다. (물론 이 경우는 global 해이기도 합니다)

반대로, $f(x)=2$인 함수가 있다면, 여기에서는 해가 여러개가 존재합니다(사실 무한대죠), 이런 경우를 weak라고 합니다.

그리고 strict 에서는 isolate라는 개념이 존재합니다.

A point $x^*$ is an isolate local minimizer if there is a neighborhood $N$ of $x^*$ such that $x^*$ is the only local minimizer in $N$

이 말은 해의 영역이 말그대로 고립(isolate)되었다는 말인데, 아래 수식을 보면 이해가 좀 쉽습니다.

$f(x)=x^4cos(\frac{1}{x})+2x^4$

위 수식의 해는 0입니다. 그런데 문제는 cos의 $\frac{1}{x}$부분입니다. x가 0으로 가면 이는 무한대가 됩니다. 무한대이기는 하지만 cos이긴 때문에 -1~1의 범위를 가지며, 반복되기 때문에, 0의 근처에서 수없이 많은 해가 존재할 수 있습니다. 이 경우는 isolate가 아닙니다. 즉 모든 strict는 isolate가 아니지만, isolate는 strict라는 조건이 성립합니다.

사실 이런 문제를 아직 접해본 적은 없어서 그냥 이런 개념이 있구나 정도로 넘어가도 좋을 듯 합니다.

Recognizing a local minimum

책에서는 2차 미분(Twice continuously differentiable)이 가능하면, local minimum이 존재한다고 합니다. $f(x)=x^2$인 경우와 $f(x)=x$인 경우를 보면, 전자는 2차 미분값이 2로 존재하지면, 후자는 1차 미분만 가능합니다.(상수를 미분하여 0이 되는 것은 제외합니다)
당연히 전자는 $x=0$이라는 해가 존재하지만, 후자는 존재하지 않습니다. 이런 의미입니다.

이를 증명하는 부분들이 간단히 언급되고 있는데 생략하겠습니다.

2. 최적화 기본 전략 2가지

구속조건이 없는 최적화는 대부분 iteration을 통해, 시작점($x_0$)에서 해($x^*$)로 찾아가는 방식입니다. 여기서 중요한 부분이 각 iteration마다 $x$를 어떻게 변화시켜 가느냐 이며, 이를 위한 방법이 크게 Line search와 True region 이 존재합니다.

Line search

$p_k$는 direction, $\alpha$는 step length입니다. iteration과정에서 $p_k$방향을 계산하고, $\alpha$ 만큼 이동하며 최적 해를 찾아가는 방식입니다.

$\displaystyle\min_{\alpha>0}f(x_k+\alpha p_k)$

아래 그림처럼, $x_k$에서 특정 벡터만큼 이동해 나가는 방식입니다.

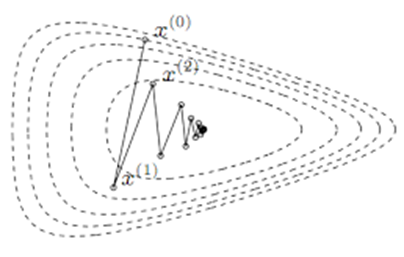
잘 알려진 Newton's Method가 Line search에 해당하는 방식입니다. (Newton's Method에서는 $\alpha$는 1입니다)

Trust region

Trust Region은 iteration과정에서 $x_k$주변의 값으로 $f$를 근사하는 model function, $m_k$를 생성하여 최적 해를 찾아가는 방식입니다. model function을 생성하는 $x_k$주변 영역을 Trust Region이라고 합니다.

$\displaystyle\min_p m_k(x_k+p)$, $x_k+p$ lies inside the trust region

통상, model function은 아래와 같이 2차 함수로 근사를 합니다.

$m_k(x_k+p)=f_k+p^T\bigtriangledown{f_k}+\frac{1}{2}p^T\bigtriangledown^2f_k$

예를 들어서, $f(x)=10(x_2-x_1^2)^2+(1-x_1)^2$ 이고 $x_k=(0,1)$이면,

$f_k=11$, $\bigtriangledown{f_k}=\begin{bmatrix}-2\\20\end{bmatrix}$, $\bigtriangledown^2f_k=\begin{bmatrix}-38 \ 0\\ 0 \ 20\end{bmatrix}$

아래 그림과 같이, 특정 구간내에서 model function, $m_k$로 근사한 이후에, $x_k$를 업데이트해 나갑니다.

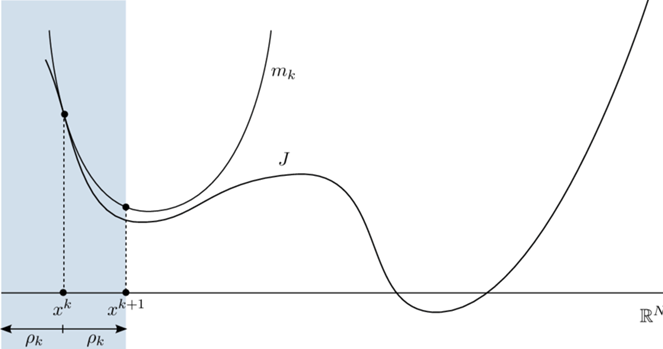
Optimization 이론 중, 정밀도 측면에서 가장 잘 알려진 방식인 Levenberg-Marquardt Method가 Trust Region에 해당합니다.

책에서는 뒤에 Line search와 Trust Region에 관련된 세부 이론들이 간략히 소개되어 있지만, 어차피 뒤에 할 예정이기 때문에 이 정도로 마무리합니다. 이번 챕터는 최적 해는 global, local이 있다. 최적 해를 구하는 방식은 크게, Line search와 Trust region이 있다 정도로만 정리하면 됩니다.