Mat 클래스 활용

Mat 객체 생성

일반적인 Mat 객체 생성

Mat img1; 	// empty matrix

Mat img2(480, 640, CV_8UC1);		// unsigned char, 1-channel
Mat img3(480, 640, CV_8UC3);		// unsigned char, 3-channels
Mat img4(Size(640, 480), CV_8UC3);	// Size(width, height)
// 모두 같은 640x480 크기의 img가 생성 된다.
// width와 height의 자리를 기억하자.

주의할 점

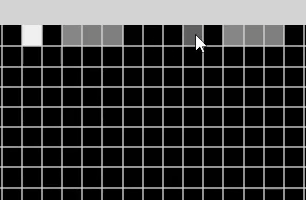
공간만 생성되고 초기화가 안 됐기 때문에, 저런 노이즈가 발생할 수 있다.
크기만 지정했다는 것을 기억하자.

Scalar를 통해 색상을 지정해 보자

Mat img5(480, 640, CV_8UC1, Scalar(128));		// initial values, 128
Mat img6(480, 640, CV_8UC3, Scalar(0, 0, 255));	// initial values, red

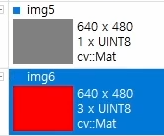
img5는 1채널 영상, img6는 3채널 영상이다. 각 스칼라 값을 확인해 보자.

1채널 Scalar(128)은 회색, 3채널 Scalar(0, 0, 255)는 빨간색 이구나.

Mat 정적 맴버 함수를 사용

Mat mat1 = Mat::zeros(3, 3, CV_32SC1);	// 0's matrix
/*
0 0 0
0 0 0
0 0 0
*/
Mat mat2 = Mat::ones(3, 3, CV_32FC1);	// 1's matrix
/*
1 1 1
1 1 1
1 1 1
*/
Mat mat3 = Mat::eye(3, 3, CV_32FC1);	// identity matrix
/*
1 0 0
0 1 0
0 0 1
*/

Scalar와 다른 인자를 지정할 수 있나?

float data[] = {1, 2, 3, 4, 5, 6};
Mat mat4(2, 3, CV_32FC1, data);

mat4는 3x2행렬이고, data의 원소가 차례로 mat4를 구성하게 된다.

/* mat4 = 
1 2 3
4 5 6
*/

이렇게 생성할 수도 있다.

Mat mat5 = (Mat_<float>(2, 3) << 1, 2, 3, 4, 5, 6);
Mat mat6 = Mat_<uchar>({2, 3}, {1, 2, 3, 4, 5, 6});
// 결과는 모두 같다.

기존 Mat객체를 재활용하고 싶을 때

creat함수를 사용.

mat4.create(256, 256, CV_8UC3);	// uchar, 3-channels
mat5.create(4, 4, CV_32FC1);	// float, 1-channel

// create함수는 값을 줄 수는 없다.
// 그러므로 뒤에서 초기화를따로 해 줘야 한다.

mat4 = Scalar(255, 0, 0);
mat5.setTo(1.f); // 모든 값을 1.f로 설정

Mat 클래스 객체의 참조 & 복사

= 연산자는 참조(얕은 복사)를, Mat::clone() 혹은 Mat::copyTo()는 깊은 복사를 수행한다.

• 예시

  // ...
  Mat img1, img2, img3, img4;
  
  img1 = imread("lenna.bmp");
  img2 = img1;
  img3 = img1.clone();
  img1.copyTo(img4); // 객체 위치 조심!
  
  img1.setTo(Scalar(0, 255, 255));	// yellow
  
  imshow("img1", img1);
  imshow("img2", img2);
  imshow("img3", img3);
  imshow("img4", img4);
  // ...

  결과
  
  img2, img3, img4에 img1을 복사한 뒤, 원본인 img1의 내용을 바꿔 보았다.
  깊은 복사(=)를 한 img2는 결과 값이 바뀌었고,
  얕은 복사(copyTo(), clone())을 한 img3, img4는 내용이 바뀌지 않았다.

Mat행렬 부분 추출

Mat img1 = imread("lenna.bmp");
Mat img2 = img1(Rect(100, 100, 340, 240));
Mat img3 = img1(Rect(100, 100, 340, 240)).clone();
// img1의 Point(100, 120)을 시작으로 Size(340, 240)크기만큼
// img2는 깊은 복사를
// img3는 얕은 복사를 수행했다.

// img2를 반전시키면
img2 = ~img2;

imshow("img1", img1);
imshow("img2", img2);
imshow("img3", img3);

결과

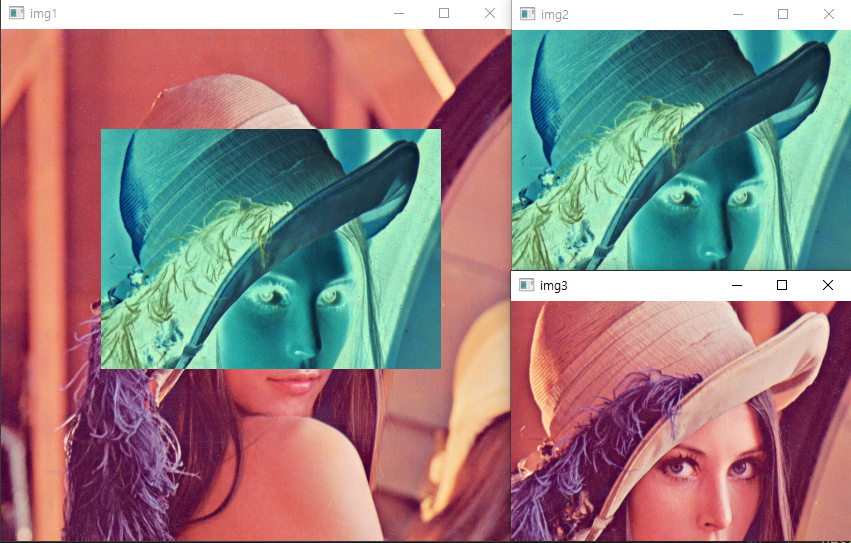
img2는 img1의 일부분을 깊은 복사했기 때문에 원본인 img1역시 일부분 반전이 수행되었다.
img3는 얕은 복사기 때문에 img1의 변화와 상관 없이 원본 모습을 유지하고 있다.

Mat 객체 값 접근하기

여러 방법이 있다.

• Mat::data : 메모리 연산이 잘못될 경우, 프로그램이 비정상 종료될 수 있음.
• Mat::at() : 좌표 지정이 직관적이고, 임의 좌표에 접근할 수 있음.
• Mat::ptr() : Mat:at()보다 빠르게 동작하고, 행 단위 연산 수행에 유리함.
• Matlterator_ : 좌표를 지정하지 않아 안전하지만, 성능은 느림.

Mat::at() 함수 사용

Mat mat1 = Mat::zeros(3, 4, CV_8UC1);

for (int y = 0; y < mat1.rows; y++) {
	for (int x = 0; x < mat1.cols; x++) {
		mat1.at<uchar>(y, x)++;
	}
}

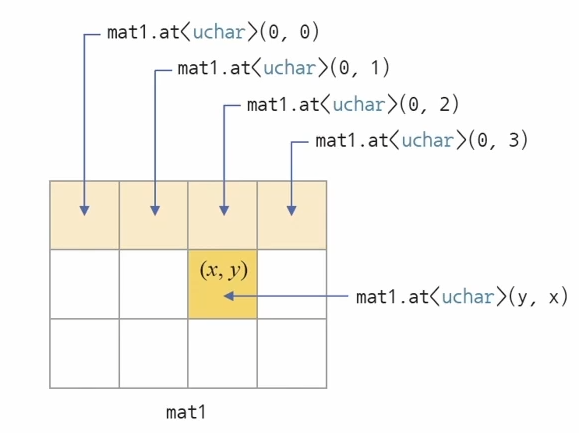
mat1.at<uchar>(y, x)가 동작하는 모습

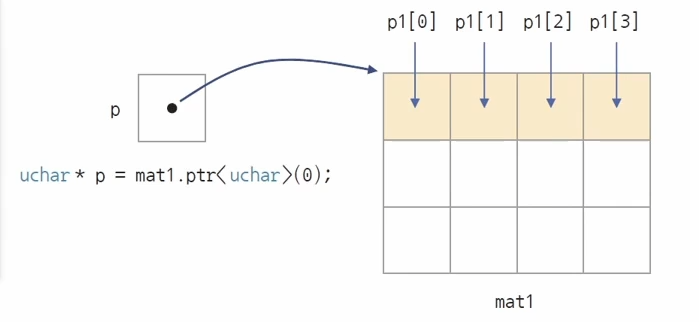
Mat::ptr() 함수 사용

Mat mat1 = Mat::zeros(3, 4, CV_8UC1);

for (int y = 0; y < mat1.rows; y++) {
	uchar* p = mat1.ptr<uchar>(y);
    
	for (int x = 0; x < mat1.cols; x++) {
		p[x]++;
	}
}

mat1.ptr<uchar>(y)가 동작하는 모습

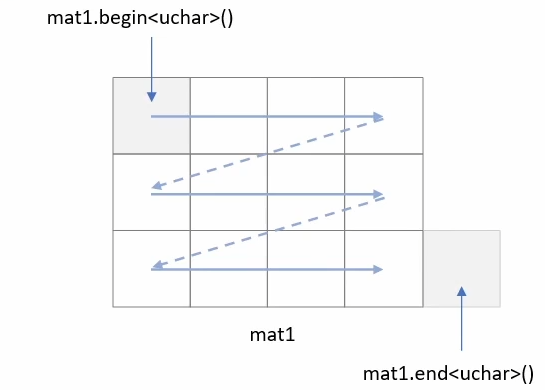
Matlterator_ 반복자 사용

Mat mat1 = Mat::zeros(3, 4, CV_8UC1);

for (MatIterator_<uchar> it = mat1.begin<uchar>(); it != mat1.end<uchar>(); ++it) {
	(*it)++;
}

MatIterator_<uchar> it가 동작하는 모습

Mat 클래스 기본 행렬 연산

• 배열 data과 Mat객체 mat을 선언하고, 기본적인 행렬 연산을 해 보자.

  float data[] = {1, 1, 2, 3};
   Mat mat1(2, 2, CV_32FC1, data);
   cout << "mat1:\n" << mat1 << endl;
   
   /* mat1:
   [1, 1;
   2, 3] */

• 역행렬(Inverse Matrix) - inv()

  Mat mat2 = mat1.inv();
  cout << "mat2:\n" << mat2 << endl;
  
  /* mat2:
  [3, -1;
  -2, 1] */

• 전치 행렬(Transpose Matrix) - t()

  cout << "mat1.t():\n" << mat1.t() << endl;
  
  /* mat1.t():
  [1,2;
  1,3] */

• 단순 사칙 연산

  cout << "mat1 + 3:\n" << mat1 + 3 << endl;
  cout << "mat1 + mat2:\n" << mat1 + mat2 << endl; // mat2 : 단위 행렬
  cout << "mat1 * mat2:\n" << mat1 * mat2 << endl;
  
  /* mat1 + 3:
  [4, 4;
  5, 6]
  
  mat1 + mat2:
  [4, 0;
  0, 4]
  
  mat1 * mat2:
  [1, 0;
  0, 1] */