경우의 수

miya·2020년 12월 28일

기초수학

목록 보기

4/6

경우의 수란 확률 통계의 기초가 되는 개념으로 어떤 사건이 발생했을 때 생기는 모든 결과의 가짓수를 말한다.

사건: 어떤 실험이나 관찰에 의하여 일어나는 결과
경우의 수: 사건이 일어날 수 있는 모든 경우의 가짓수
예) 주사위 한개를 던졌을 때, 짝수 눈이 나오는 경우(사건)는 2,4,6 3가지(경우의 수)이다.

이러한 경우의 수에도 합의 법칙과 곱의 법칙이 존재하는데, 두 사건 A, B가 동시에 일어나지 않을 때, 즉 사건 A 또는 사건 B가 일어날 경우의 수를 구하는것이 합의 법칙이다.
두 사건 A, B에 대하여 동시에 일어나는 경우의 수를 곱의 법칙이라고 한다.
예) 지역 A에서 B로 갈 방법은 지하철 노선이 3가지 버스 노선이 4가지이다. 이때 버스 또는 지하철을 타고갈 경우의 수는 총 7가지로 합의 법칙에 해당한다.
예) 지역 A에서 B로 갈 방법이 2가지 B에서 C로 갈 방법이 3가지 있을 경우, 지역 A에서 B를 거쳐 C로 가는 모든 경우의 수는 2x3으로 총 6가지이며 이는 곱의 법칙에 해당한다.(A에서 B로 가는 사건과 B에서 C로 가는 사건이 동시에 발생해야한다.)

순열(Permutation)

순열이란 서로 다른 n개에서 r(0<r≤n)개를 택하여 일렬로 나열하는 것을 말하며 $_nP_r$ 로 나타낸다.
순열의 개수는 $_nP_r$ = n(n-1)(n-2)×･･･×(n-r+1) 으로 구할 수 있다.
예) A,B,C,D,E의 5개 문자에서 3개를 택하여 일렬로 나열하는 총 개수는 위의 공식을 사용하면(5x4x3=60) 60개임을 알 수 있다.
만약 n개에서 n개의 순열을 구한다면 $_nP_n$ = n(n-1)(n-2)×･･･×(n-n+1) 로 n!이라고 쓰고 n팩토리얼로 읽는다.

원순열

원순열이란 서로 다른 것을 원형으로 배열하는 순열이다.

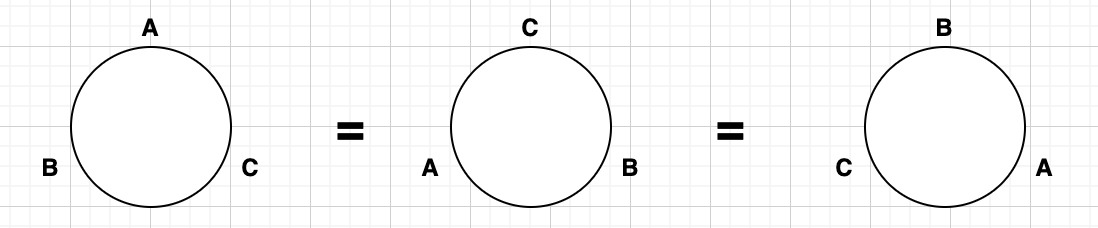
예를 들어 원형 탁자에 A,B,C 세명이 앉아있다고 생각해보자. 원형 탁자 3명을 배치할 경우 ABC, BCA, CAB 의 순서가 같아(원형이기때문) 같은 경우가 3개씩 존재한다. 따라서 n!/3 으로 (n-1)! 과 같다.

문제1) 정삼각형 모양의 탁자의 한 변에 2명씩 6명이 둘러앉는 경우의 수
1. 원형으로 6명이 둘러앉는 경우의 수 = (6-1)!
2. 회전시켰을 때, 겹치지 않는 서로 다른 경우의 수 = 2
=> (6-1)! 2
=> n명이 한 변에 k명씩 정다각형 모양의 탁자에 앉는 경우의 수는 k(n-1)!

문제2) 남학생 3명과 여학생 2명이 원형의 탁자에 둘러앉을 때, 여학생 2명이 이웃하여 앉는 경우의 수
1. 이웃하는 여학생 2명을 1명으로 가정한 후 경우의 수 = (4-1)!
2. 여학생끼리 자리를 바꾸는 경우의 수 = 2!
=> 3! * 2!

중복순열

중복순열이란 서로 다른 n개에서 중복을 허용하여 r개를 택하여 일렬로 나열하는 순열이다. 이 중복순열의 수를 기호로 $_n\Pi_r$ 와 같이 나타낸다. 예를 들어 문자 a와 b중에서 3개를 택하는 중복순열을 생각하면, aaa, aab, aba, abb, baa, bab, bba, bbb 의 8가지 경우가 나온다.

{_n{\Pi}_r} = n^r

문제1) 3개의 숫자 0, 1, 2로 중복을 허용하여 만들 수 있는 두 자리 자연수
1 : 10, 11, 12
2 : 20, 21, 22
=> (3-1)* $_3\Pi_{2-1}$

문제2) 5개의 문자 a, b, c, d, e 중에서 중복을 허용하여 4개를 택하고 일렬로 나열할 때, a와 b가 반드시 포함되는 경우의 수
1. 중복을 허용하여 4개를 택하고 일렬로 나열 할 경우 : $_5\Pi_4$
2. a가 포함되지 않은 경우의 수 : $_4\Pi_4$
3. b가 포함되지 않은 경우의 수 : $_4\Pi_4$
4. a, b가 모두 포함되지 않은 경우의 수 : $_3\Pi_4$ (2와 3의 중복)
=> $_5\Pi_4 - (_4\Pi_4+_4\Pi_4 -_3\Pi_4)$ = 194

Python으로 permutation 구현하기

python으로 순열의 아이템들을 구하는 함수를 구현해본것이다. 파이썬에서는 라이브러리를 제공하여 쉽게 순열의 모든 아이템들을 구할 수 있다. 다만, 라이브러리를 사용하지 못해 직접 구현해야할 경우는 아래의 구현코드를 참고하기 바란다.

1. Python 라이브러리 활용(itertools 라이브러리)

    from itertools import permutations
    l = list(map(''.join, permutations('ABCD',2)))
    print(l)

2. 직접 구현

직접 구현을 하기 위해서 개념을 이해해야한다. recursive 방식을 활용하면 permutation([1,2,3,4])는 ([1+permutation[2,3,4]....], [2+permutation[1,3,4]....])로 반복된다. 이를 간단하게 구현하면 아래와 같다.

def permutation(items):
    out = []
    if len(items) == 1:
        return items

    for i , let in enumerate(items):
        for perm in permutation(items[:i] + items[i+1:]):
            out += [str(let) + str(perm)]
    return out

유사하지만 dfs 방식을 활용하면 아래와 같다.

def permutation(items, r=0):
    result = []
    prev = []

    def dfs(elements):
        if (len(elements)-r) == 0:
            result.append(copy(prev))
        
        for idx, e in enumerate(elements):
            prev.append(e)
            dfs(elements[:idx]+elements[idx+1:])
            prev.pop()

    dfs(items)

    return result

조합(Combination)

조합은 서로 다른 n개에서 순서를 생각하지 않고 r(0<r≤n)개를 택하는 것을 조합이라고 하며, 이는 nCr 로 표시한다.
조합의 수는 nCr = nPr / r! = n!/r!(n-r)! 으로 구한다.
순열은 순서를 생각하여 일렬로 나열하는 것이고 조합은 순서를 생각하지 않기 때문에 (A, B, C)와 (C, B, A)는 순열에서는 다른 경우로 보지만 조합에서는 같은 경우라고 생각한다.

Python으로 combination 구현하기

아래는 python으로 조합의 아이템들을 나열해주는 함수를 구현한 것이다. 단순 갯수만 구해야한다면 수식을 계산하는 함수를 구현하는 것이 빠를것이다. 아이템을 구해야할 경우에만 구현하면 된다.

1.Python 라이브러리 활용(itertools 라이브러리)

    from itertools import combinations
    l = list(map(''.join, combinations('ABCD',2)))
    print(l)

2. 직접 구현

def combinations(n, r):
    output = []
    def backtrack(first=1, cur=[]):
        if len(cur) == r:
            output.append(copy.copy(cur))

        for i in range(first, n+1):
            cur.append(i)
            backtrack(i+1, cur)

            cur.pop()
    backtrack()

    return output