[청년취업사관학교 새싹]핀테커스 수업 7주차(10/10)

<수업 내용>

KNN(K-Nearest Neighbor) 알고리즘 개념

• Feature Space :주어진 데이터의 features를 바탕으로 target data의 분포 표현
• K-Nearest : 새로운 데이터의 features가 주어 졌을 때 가장 거리가 가까운 K개의 data의 target 값을 확인하여 다수결에 따라 새로운 데이터의 target data를 정의내린다
  • 거리 : Euclidean distance, Manhattan distance 비교 예시

def euclidean(A,B):
  return ((A[0]-B[0])**2+(A[1]-B[1])**2)**(1/2)

def manhattan(A,B):
  return abs(A[0]-B[0])+abs(A[1]-B[1])
  
d12=(5,2.5)
d5=(2.75,7.5)
d17=(5.25,9.5)

print(euclidean(d12,d5))

print(euclidean(d12,d17))

print(manhattan(d12,d5))

print(manhattan(d12,d17))

>>
5.482928049865327
7.00446286306095
7.25
7.25
  

• 위 코드를 보아 d12,d5와 d12,d17의 manhattan 거리는 같은데, eudlidean 거리가 차이가 있다
• euclidean 거리는 features간의 차이를 더 확연하게 반영하여 나타낸다
• KNN알고리즘에서 거리는 Euclidean distance를 사용한다
• Hyper parameter (K값)은 사람이 직접 조정한다. 적절한 값을 찾아내는 것을 최적화(Optimization)이라 한다
• decision boundary : K값에 따라서 새로운 data의 target값을 정해주는 경계

KNN Algorithm 구현하기

1. 데이터 셋 생성

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(22)
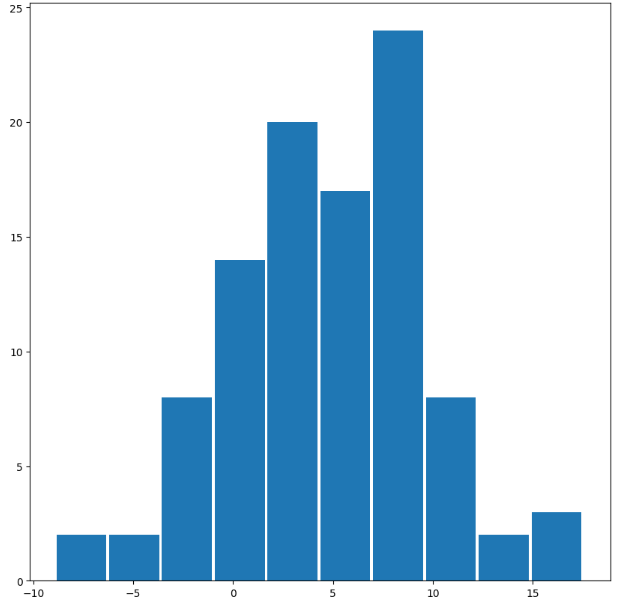
x_data=np.random.normal(5,5,100)

fig,ax =plt.subplots(figsize=(10,10))

ax.hist(x_data,width=2.5)

data=np.random.normal(loc=[5,3],scale=[1,1],size=(100,2))
print(np.mean(data, axis=0))
print(np.std(data, axis=0))

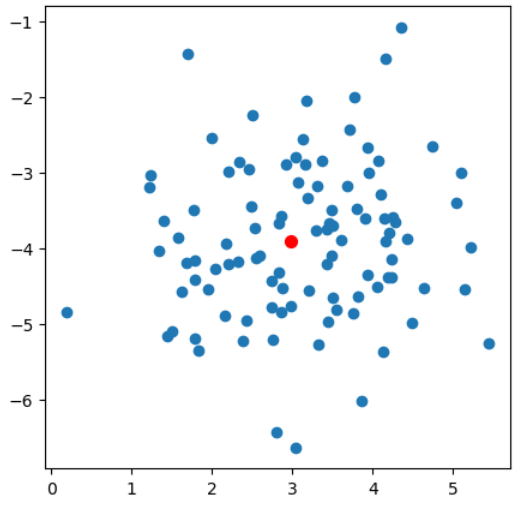
centroid=np.random.uniform(-5,5,size=2)
data=np.random.normal(centroid,1,size=(100,2))
fig,ax=plt.subplots(figsize=(5,5))
ax.scatter(data[:,0],data[:,1],)
ax.scatter(centroid[0],centroid[1], c='red', marker='o', s=50)

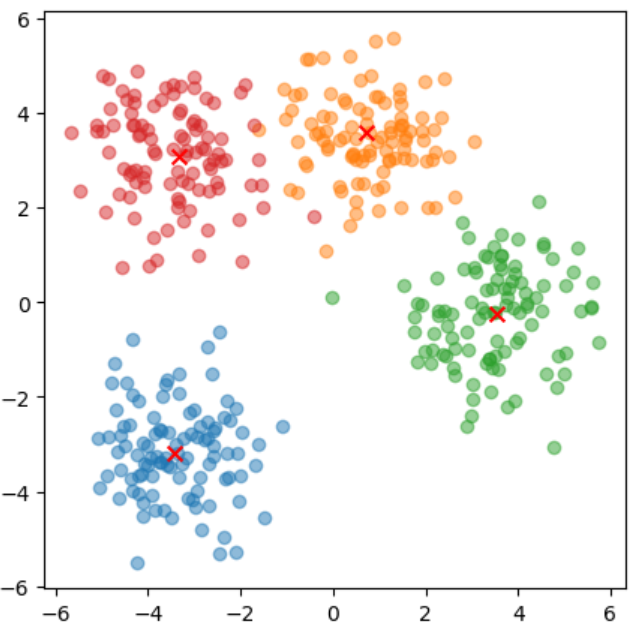
n_class=4
n_data=100

centroid_x=np.random.uniform(-5,5,size=n_class)
centroid_y=np.random.uniform(-5,5,size=n_class)

fig,ax=plt.subplots(figsize=(5,5))
data_set=[]
for i in range(n_class):
  data=np.random.normal([centroid_x[i],centroid_y[i]],1,size=(n_data,2))
  data_set.append(data)
  ax.scatter(data_set[i][:,0],data_set[i][:,1],alpha=0.5)
  ax.scatter(centroid_x[i],centroid_y[i], c='red', marker='x', s=50)

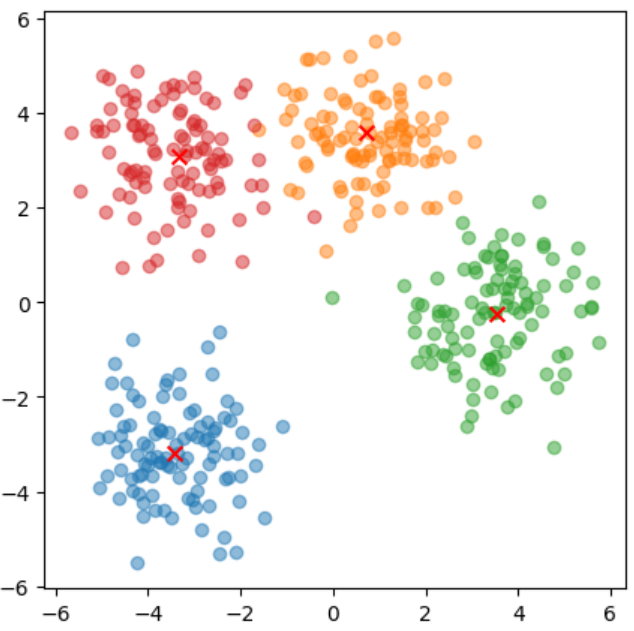
정답 예시

오늘까지 종합

n_class=4
n_data=100


centroid_x=np.random.uniform(-5,5,size=n_class)
centroid_y=np.random.uniform(-5,5,size=n_class)

fig,ax=plt.subplots(figsize=(5,5))
data_set=[]
for i in range(n_class):
  data=np.random.normal([centroid_x[i], centroid_y[i]], 1, size=(n_data, 2))
  data_set.append(data)
  ax.scatter(data_set[i][:,0] ,data_set[i][:,1], alpha=0.5)
  ax.scatter(centroid_x[i], centroid_y[i], c='red', marker='x', s=50)
features=np.vstack(data_set)
print(features.shape)

n_classes = 4
n_data = 100
target = []
for class_idx in range(n_classes):
 data_ = np.full((100,), class_idx)
 target.append(data_)
target = np.hstack(target)
print(target)

test_data=np.random.uniform(-10, 10, size=2)

euclidean=[]
for i in range(len(features)):
  distance=((test_data[0]-features[i][0])**2+(test_data[1]-features[i][1])**2)**(1/2)
  euclidean.append(distance)

print(euclidean)

K=5
def find_class(K):
  idx_distance=np.argsort(euclidean)

  idx_min_distance=[]
  for j in range(K):
    indices = np.where(idx_distance == j)
    idx_min_distance.append(indices)  

  test_target=[]
  for i in idx_min_distance:
    test_target.append(target[i])

  uniques, cnts = np.unique(test_target, return_counts=True)

  return uniques[np.argmax(cnts)]

print(find_class(5))
ax.scatter(test_data[0],test_data[1], c='purple', marker='o', s=50)
ax.text(test_data[0],test_data[1],s=f'class{find_class(5)}')

x_lim=ax.get_xlim()
y_lim=ax.get_ylim()

X=np.linsapce(x_lim[0],x_lim[1],100)
Y=np.linsapce(y_lim[0],y_lim[1],100)

for i in range(100):
  X[i],Y[i]