정렬되지 않은 리스트에서 heap을 이용하여 빠르게 중앙 값을 찾는 방법에 대해 알아보자.
힙(Heap) 자료구조와 파이썬으로 최대 힙 / 최소 힙을 구현하는 방법에 대한 설명은 우선순위 큐(Priority Queue)와 힙(Heap)게시글을 참고하면 된다.

⭐️ 중앙값(Median)

• 어떤 배열을 정렬했을 때 정 가운데에 위치하는 값
  • 예를들어, [1, 2, 3]의 배열에서는 2가 중앙값이다.
• 원소의 개수가 짝수인 경우엔, 가운데 두 원소의 평균이 중앙값이 된다.
  • [1, 2, 3, 4]에서는 2와 3의 평균인 2.5가 중앙값이다.

중앙값(Median) 찾기

• 중앙값은 정렬된 배열에서 찾아야 하므로 가장 먼저 정렬을 수행해야 한다.
• 정렬 후엔, 단순히 배열 크기의 절반에 해당하는 인덱스에 접근해 반환하면 된다.
• Python에서는 내장 함수인 sorted()를 사용하여 배열을 정렬할 수 있다.
• sorted() 함수를 사용하여 중앙값을 찾는 코드를 작성하면 다음과 같다.

def find_median(arr):
    n = len(arr)
    sorted_arr = sorted(arr)
    if n % 2 == 0:
        # 짝수 개의 요소를 가지는 배열에서 중앙값은 가운데 두 요소의 평균
        return (sorted_arr[n//2-1] + sorted_arr[n//2]) / 2
    else:
        # 홀수 개의 요소를 가지는 배열에서 중앙값은 가운데 요소
        return sorted_arr[n//2]

• 이 코드는 배열을 정렬한 다음, 배열의 길이가 홀수인 경우 중앙 요소를, 짝수인 경우 중앙 두 요소의 평균을 반환한다.
• sorted() 함수는 평균 시간 복잡도 O(nlogn)으로 동작하므로 이 코드의 전체 시간 복잡도는 O(nlogn)이다.

실시간으로 중앙값(Running Median) 찾기

• 실시간으로 중앙값을 찾는 경우, 입력이 계속해서 들어오는 데이터 스트림에서 중앙값을 찾아야 한다.
• 이런 경우에는 sort를 사용하는 것보다 heap을 사용하는 것이 더 유리하다.

이유는 다음과 같다.

• heap을 사용하여 중앙값을 찾는 경우, 입력 값이 들어올 때마다 O(logn)의 시간 복잡도로 중앙값을 찾을 수 있다.
  • 즉, 입력값의 크기와 상관없이 항상 일정한 시간 복잡도를 보장한다.
• 반면, sort를 사용하여 중앙값을 찾는 경우, 입력이 들어올 때마다 배열을 정렬해야 한다.
  • 정렬하는 데는 최악의 경우 O(nlogn)의 시간 복잡도가 걸리므로, 입력값의 크기가 커질수록 중앙값을 찾는 데 걸리는 시간이 더 많아진다.
• 또한 heap을 사용하여 중앙값을 찾는 경우, min-heap과 max-heap을 유지하면서 중앙값을 찾으므로, 중앙값을 계산하는 데 필요한 메모리 공간도 상수로 유지된다.
• 하지만 sort를 사용하여 중앙값을 찾는 경우, 배열을 정렬해야 하므로, 정렬에 필요한 추가적인 메모리 공간이 필요하다.

⭐️ heap을 사용하여 중앙값 찾기

알고리즘

• Max heap은 최대값에 바로 접근할 수 있다.
• Min heap은 최소값에 바로 접근할 수 있다.

Heap의 두 성질을 이용하여, 중앙값보다 작은 값들은 Max heap에, 중앙값보다 큰 값들은 Min heap에 저장하는 방식으로 중앙값을 찾는 알고리즘을 구현할 수 있다.

• min-heap과 max-heap을 각각 생성한다.
• 입력된 값을 차례대로 min-heap과 max-heap에 넣는다.
  • max_heap과 min_heap의 크기가 같다면 max_heap에 값을 넣는다.
  • 개수가 다르면 이전에 최대 힙에 넣은 것이기 때문에 개수 맞춰주기 위해 최소 힙에 값을 넣는다.
• 두 heap의 root 값을 각각 가져와서 (최대 값) max-heap의 root 값과 (최소 값) min-heap의 root 값을 비교한다.
• 만약 max-heap의 root 값이 min-heap의 root 값보다 크다면, 두 값을 교환한다.
• 원소의 개수가 홀수개라면 중앙 값은 max-heap의 root 값이다.
• 원소의 개수가 짝수개라면 max-heap의 root 값과 min-heap의 root값의 평균이 중앙값이다.

그림을 통해 자세히 이해해보자.

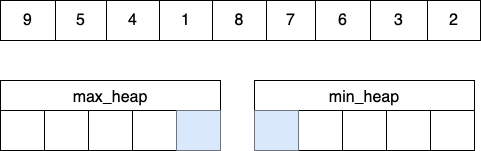
STEP 0

• 배열 [9, 5, 4, 1, 8, 7, 6, 3, 2]에서 중앙값을 찾으려고 한다.
• 파란색 박스는 각각의 root 값을 의미한다.

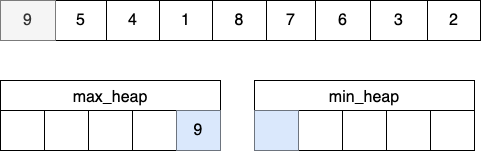
STEP 1

• max_heap과 min_heap의 크기가 같다면 max_heap에 값을 넣는다.

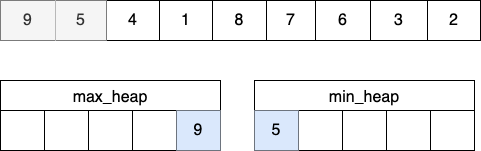
STEP 2

• max_heap과 min_heap의 크기가 다르면 이전에 최대 힙에 넣은 것이기 때문에 개수를 맞춰주기 위해 최소 힙에 값을 넣는다.

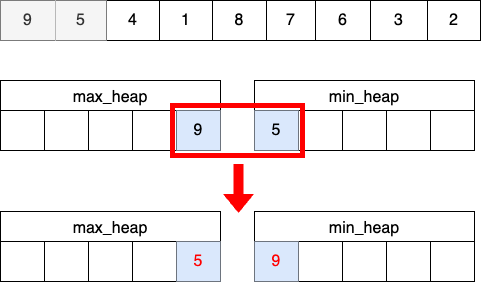
STEP 3

• 각 root 값의 대소를 비교한다.
• min_heap의 root 값이 max_heap의 root 값보다 작다면 두 수를 바꿔준다.

STEP 4

• 4, 1을 각각 max_heap과 min_heap에 넣고 STEP 1 ~ STEP 3을 반복한다.
• max_heap, min_heap 성질에 따라 숫자가 정렬된다.

STEP 5

• 홀수 번째 숫자를 넣고난 이후에는 max_heap의 root 값이 항상 중앙 값이다.

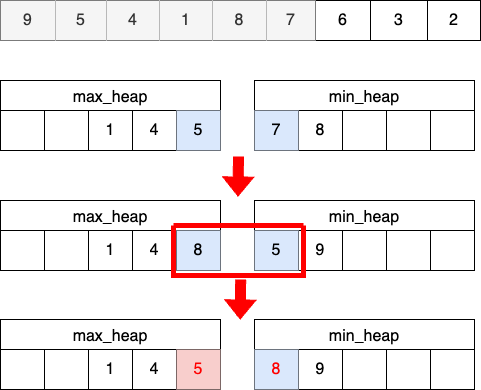
STEP 6

• 짝수 번째 숫자를 넣고난 이후에는 max-heap의 root 값과 min-heap의 root값의 평균이 중앙값이다.

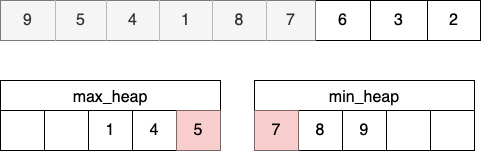
STEP 7

• 남은 숫자들을 전부 규칙에 따라 넣으면 최종 중앙 값을 찾을 수 있다.

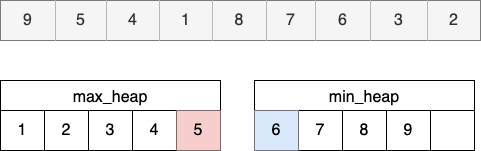
코드 작성

• 위 알고리즘을 코드로 작성하면 다음과 같다.

from heapq import heappop, heappush

max_heap = []
min_heap = []

# 규칙에 맞게 heap에 숫자 넣는 함수
def push_num(num):
    # max_heap과 min_heap의 크기가 같다면 max_heap에 값을 넣는다.
    if len(max_heap) == len(min_heap):
        heappush(max_heap, -num)
    # max_heap과 min_heap의 크기가 다르면 이전에 최대 힙에 넣은 것이기 때문에
    # 개수를 맞춰주기 위해 최소 힙에 값을 넣는다.
    else:
        heappush(min_heap, num)

    # 대소 조건 비교하기
    # min_heap의 root 값이 max_heap의 root 값보다 작다면 두 수를 바꿔준다.
    if min_heap and -max_heap[0] > min_heap[0]:
        temp_min = heappop(min_heap)
        temp_max = heappop(max_heap)
        heappush(max_heap, -temp_min)
        heappush(min_heap, -temp_max)

# 중앙 값 찾는 함수
def find_median():
    if len(max_heap) == len(min_heap):
        return (-max_heap[0] + min_heap[0]) / 2
    else:
        return -max_heap[0]

• 이제 실시간으로 중앙 값을 빠르게 파악할 수 있다.
  • 살펴본 예시를 통해 코드를 테스트한 결과는 다음과 같다.

arr = [9, 5, 4, 1, 8, 7, 6, 3, 2]
for i in range(9):
    push_num(arr[i])
    print(find_median())

9
7.0
5
4.5
5
6.0
6
5.5
5

💫 문제 추천

• 백준 1655번 - 가운데를 말해요
• 백준 2696번 - 중앙값 구하기

📍 References

• https://o-tantk.github.io/posts/finding-median/
• https://peisea0830.tistory.com/59