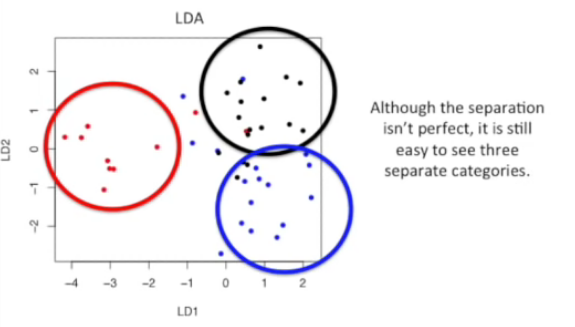
Linear Discriminant Analysis (LDA) is like PCA, but it focuses on maximizing the separatibility among known categories
간단한 예시:
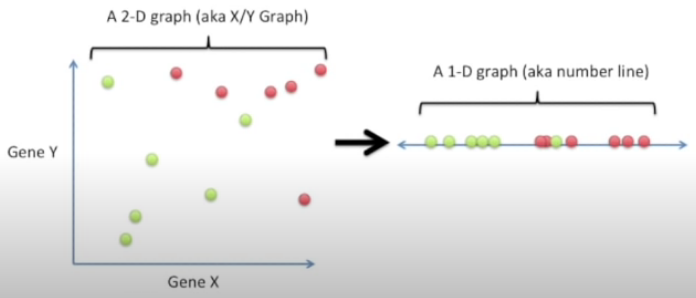
2D 그래프를 1D 그래프로 reduce 해보겠다.
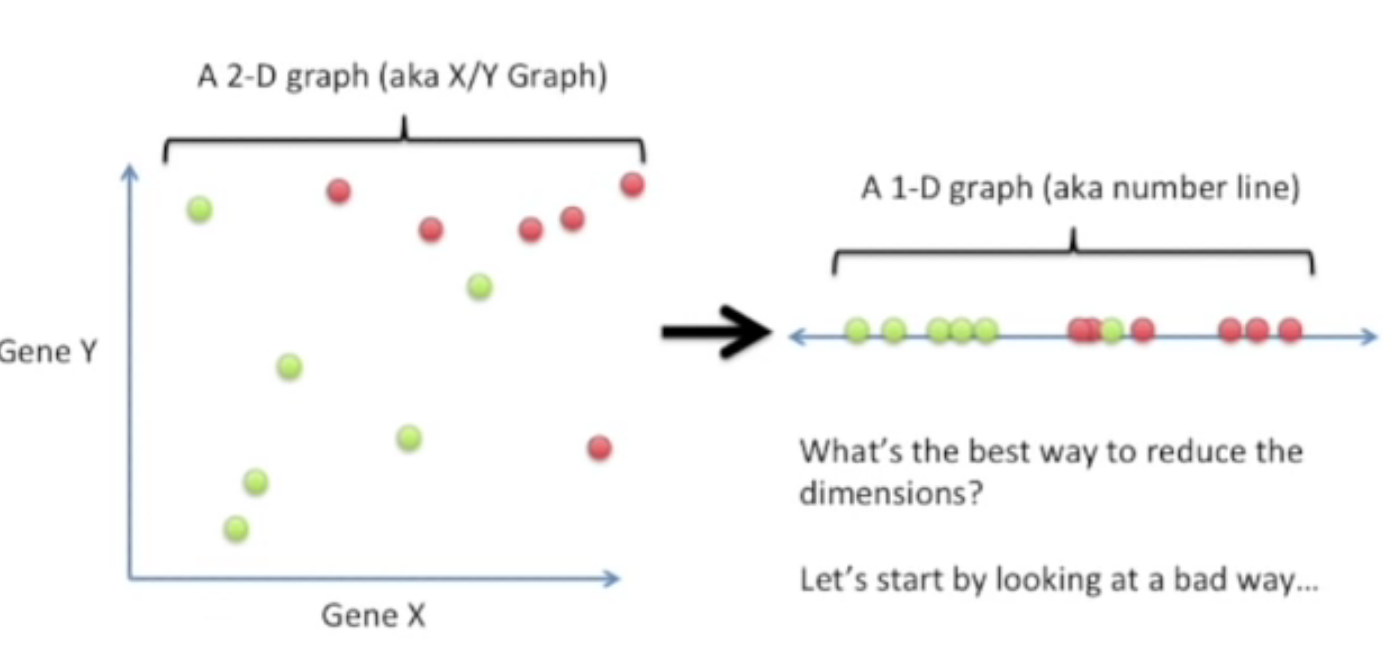
Y축을 무시하고 모든 점들을 X축으로 그대로 내려버려 1D로 만들수 있지만 이것은 안좋은 방법이다. (Y축의 모든 정보들이 소실 될 위험이 있다.)
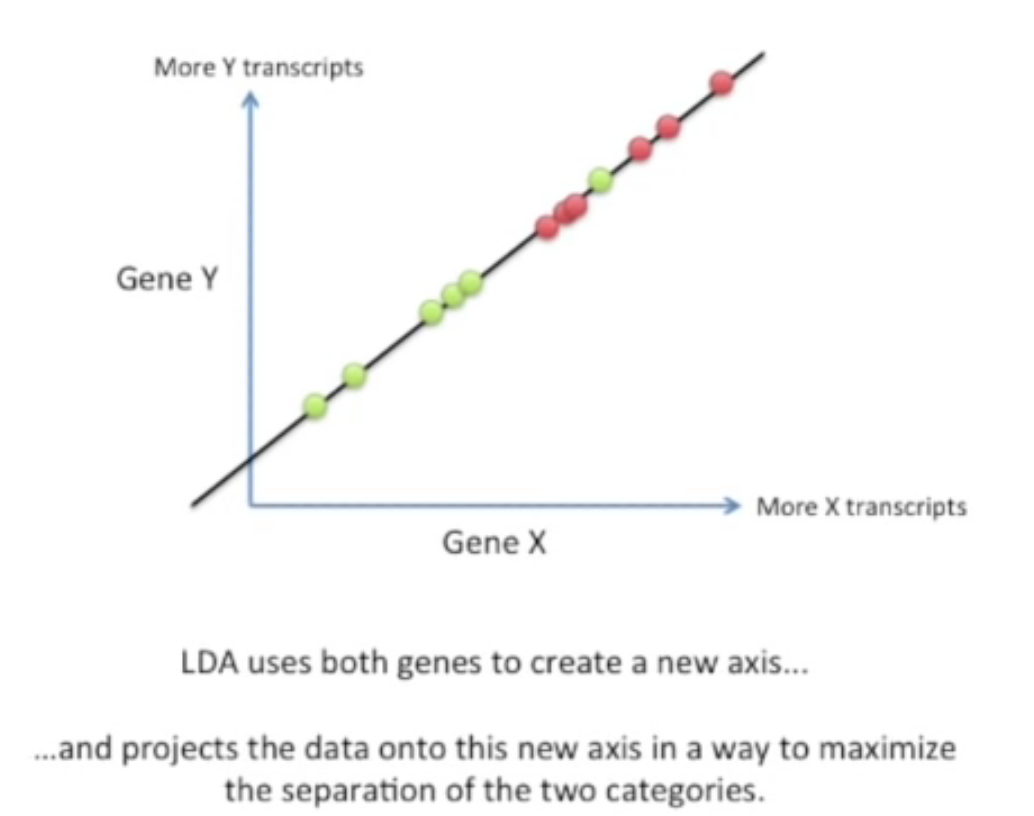
LDA는 그러한 문제를 해결하고자 두개의 축을 모두 사용하여 새로운 축을 생성한다. 그리고 데이터를 그 축에 투영시켜 두가지 카테고리가 가장 효율적이게 분리될 수 있도록 한다.
LDA의 원리
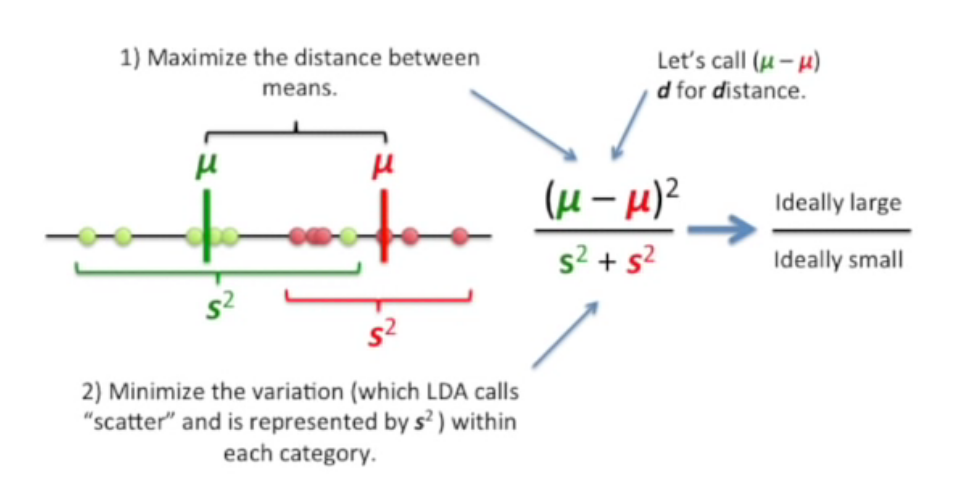
1) 각 카테고리의 평균값을 최대화하여 분자로 둔다. 위 사진에서는 μ로 표현되어 있다. (이 때 제곱을 하는 이유는 어떤 카테고리의 평균값이 더 클지 모르기 때문. 즉, 음수값을 나타내지 않게 하기 위함)
2) 각 카테고리에 있는 데이터들의 (최댓값-최솟값) 을 s (scatter) 라고 두자. 분산을 최소화 시켜 분모로 둔다.
d와 s가 둘 다 중요한 이유
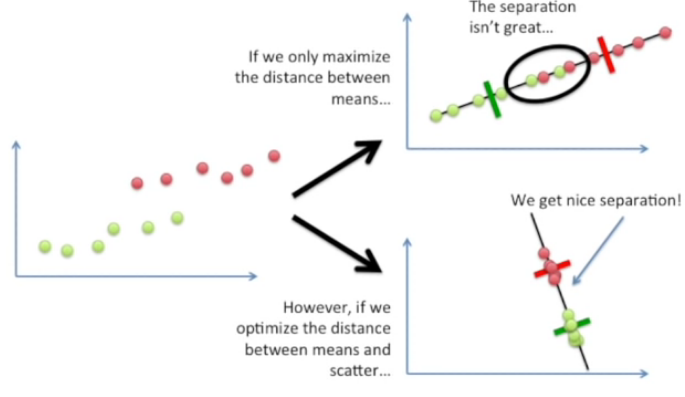
만약 평균값 사이의 거리만을 최대화 하게 된다면 분리가 적절치 못함을 확인할 수 있다.
그러므로 우리는 평균값과 scatter 사이의 거리를 최적화 시켜 적절하게 카테고리를 나눌수 있는 axis를 찾을 수 있다.
만약에 카테고리가 2개 이상이라면?
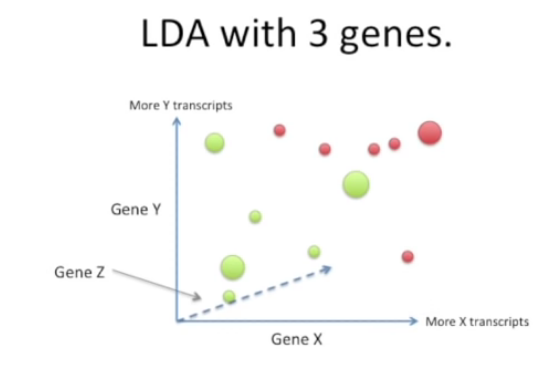
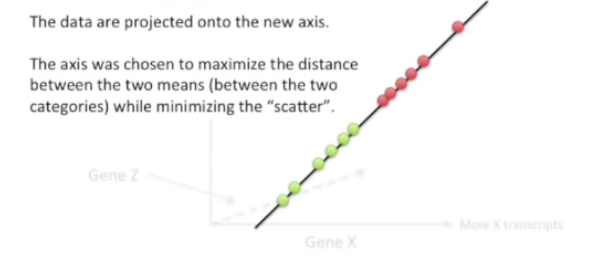
원리는 똑같다.
- 평균값들의 거리는 최대화하고 scatter는 최소화하는 축을 찾아보자
그러나 전의 과정과는 다른 부분들이 있다.
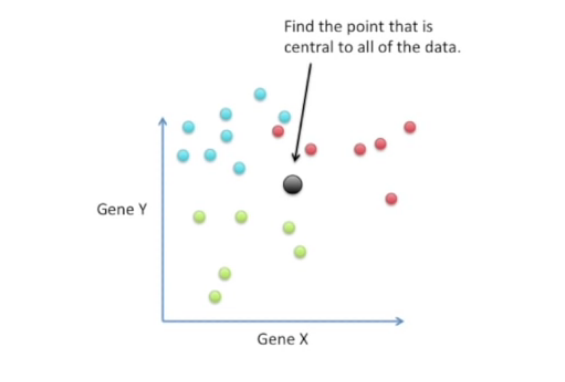
1) 우선 모든 데이터들로부터 중심에 있는 point를 찾아야 한다.
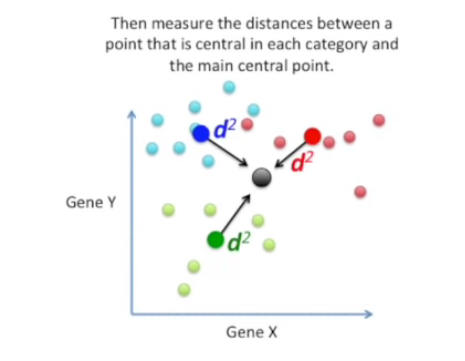
2) 그리고 중심 point와 각 카테고리별 중심에 있는 point의 거리를 구한다.
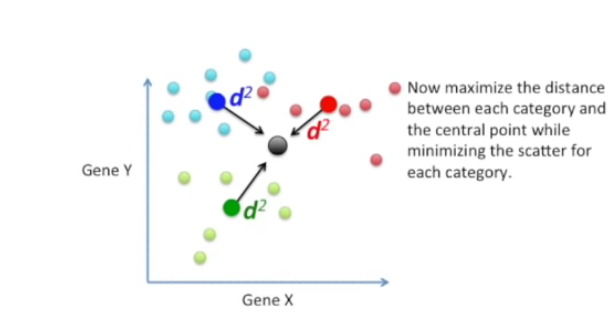
3) 중심 point와 각 카테고리별 데이터가 최대화되면서 scatter는 최소화시킨다.
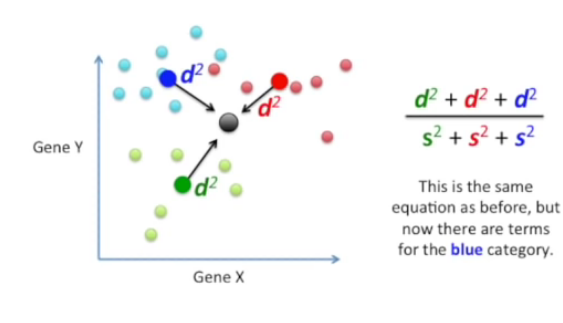
4) 데이터를 두가지 카테고리로 나눌때의 식과 똑같지만 3번째 카테고리를 위한 변수가 추가되었다.
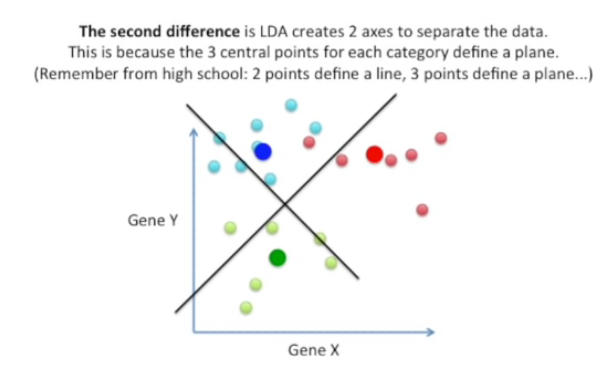
5) 또 다른 차이점은 3개의 카테고리로 분리할려면 축이 2개가 필요하다는 점이다. 분리하고자하는 카테고리가 늘어날수록 축의 수는 증가하게된다.