Algorithm - 2. Insertion Sort

무순리스트 기반 구현인 선택 정렬과 달리 삽입 정렬은 순서리스트에 기반한다.

Insertion Sort

매를 먼저 맞는,
우선순위 큐가 순서리스트로 구성되는 삽입 정렬을 알 아 보 자

실행 시간

insert()

• N회의 insert 작업
• 삽입 시에 최초 O(1) - 마지막 O(N)
• 1 + 2 + ... + (N-1) + N
• N*(N-1) / 2

remove()

• N회의 remove 작업
• 1회에 상수 시간 소요

최종적으로 O(N^2) 시간 소요된다.

제자리 삽입 정렬

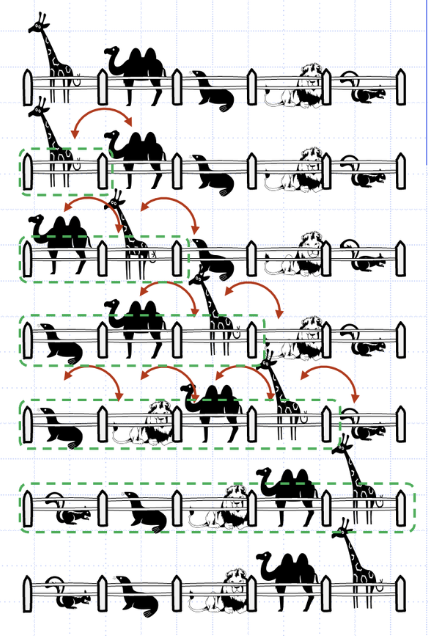
리스트의 앞 부분을 정렬 상태로 유지하면서 뒤 인덱스에 접근해간다. 새로운 원소가 들어오게 되면 정렬 위치를 찾아 삽입해나간다.

다음은 제자리 삽입 정렬의 의사코드다.

Alg inPaceInsertSort(A)
	input array A of N keys
    output sorted array A
    
for(idx <- 1 to N-1){
	insertElem <- A[idx]
    j <- idx-1
	while( (j >= 0) & (A[j] > insertElem) ){
    	A[j+1] <- A[j]
        j <- j-1
    }
    A[j+1] <- insertElem
}
return

for문의 인덱스는 1부터 시작한다. 비교를 통해 A[idx]가 어디에 들어갈지를 확인하게 되는데, idx 0의 경우 정렬 섹션에 원소가 오직 하나이기 때문에 별다른 작업이 필요없다.

insertElem에는 A[idx]를 저장하고 j는 idx-1을 저장한다. 0 ~ idx-1까지 정렬 데이터가 있고 정렬 데이터 끝부터 인덱스가 내려오면서 A[j]와 insertElem을 비교한다. insertElem보다 클 경우 A[j]를 뒤로 한 칸 밀어버린다. 그렇게 계속 밀고 가다가 어느 순간 A[j]가 insertElem보다 작게 될 것이다. 그 때 insertElem은 A[j]의 바로 뒤에 삽입한다.

성능

내부와 외부 반복문 모두 O(N)의 시간복잡도로 삽입 정렬의 전체 시간복잡도는 O(N^2)다.

선택 정렬 vs 삽입 정렬

삽입 정렬이 선택 정렬에 비해 조금 나을 수 있는 환경은 초기 데이터가 거의 정렬이 된 경우다. 정렬된 데이터의 경우 삽입 정렬은 내부 반복문에서 O(1)이 걸려 전체 O(N) 정도로 성능이 나아진다. 하지만, 선택 정렬은 데이터를 선택하는 횟수, 데이터를 선택하기 위한 데이터 간의 비교는 여전히 N, N회다.

선택 정렬이 더 나을 수 있는 환경은 뭐가 있을까? 초기 데이터가 역순으로 정렬이 된 경우다. 역순의 데이터를 삽입 정렬한다고 했을 때, 원소 간의 swap()연산이 매번 O(N)시간 이루어지게 된다. swap 작업이 비싸지면 삽입 정렬의 부담이 더 커지게 된다.

참고 : 국형준. 알고리즘 원리와 응용. 21세기사, 2018.