HuggingFace Deep RL Course - 2. Q-Learning

참고 링크: https://huggingface.co/deep-rl-course/unit2/introduction?fw=pt

policy

• agent의 의사결정 단계(일종의 brain)를 policy라고 일컬음
• 어떠한 상태(state)가 주어지면 기대되는 누적 보상(reward)을 최대화하는 방향의 행동(action)을 취하게 함
• 최적의 policy를 찾는 방법으로는 크게 policy-based methods, value-based methods가 존재

policy-based methods

• 주어진 상태에서 어떤 행동을 취할지 policy를 직접적으로 학습
• policy는 neural network
• value function이 없음
• policy를 직접 정의하는 것이 아니라 학습을 통해 정의됨

value-based methods

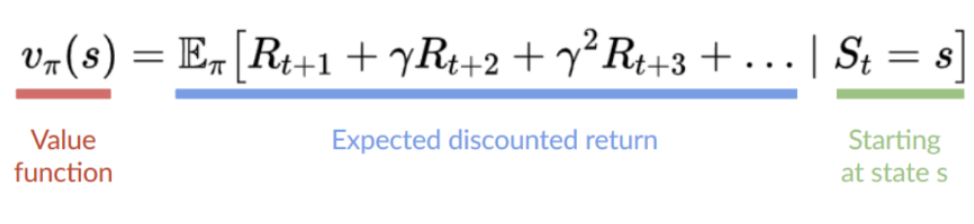
• 어떤 상태가 더욱 가치있는지를 배우는 value function을 학습하고 해당 value function을 이용해 행동을 선택
  • 상태(state)와 기대값(expected value)를 매핑하는 value function을 학습
• policy가 학습되지 않기 때문에 미리 직접 function을 지정(specify)해줘야 함
  • e.g. 언제나 최대의 보상을 야기하는 행동을 취하게 하고 싶다면 greedy policy 생성
  • 대개 exploration-exploitation trade-off를 다루는 epsilon-greedy policy 사용
• value function이 neural network
  • 최적의 value function이 최적의 policy를 얻도록 함

state-value function

• 각 state에서, 에이전트가 해당 state에서 시작해 policy를 따를 때 얻을 수 있는 기대값(expected return)을 리턴
• state S_t의 값을 계산

action-value function

• 각 state-action 쌍에서, 에이전트가 해당 state에서 시작해 행동을 취하고 policy를 따를 때 얻을 수 있는 기대값(expected return)을 리턴
• state-action 쌍 (S_t, A_t)의 값을 계산 (해당 state에서 행동을 취할 때의 값을 계산)

Bellman Equation

• 앞서 소개한 state value, state-action value의 계산을 간편하게 도와주는 방법
  • 특정 state에서 시작해 이후의 값을 모두 계산해서 더해주는 방식은 반복적이고 지루

• Dynamic Programming과 유사하게, 즉각적인 reward인 R_t+1와 다음 state의 discounted value의 합을 이용해 표현

Learning Strategies

• RL agent는 환경과 상호작용하면서 학습을 진행하는데, 이는 경험과 보상이 주어지면 agent가 value function 혹은 policy를 업데이트할 수 있다는 아이디어와 연관
• Monte Carlo와 Temporal Difference는 value function, policy function을 학습할 수 있는 두 가지 전략

Monte Carlo

• 에피소드가 마무리된 이후 value function을 업데이트
  • (state, actions, rewards, next states)의 리스트가 존재할 때 모든 보상을 더해 G_t를 계산하고 이를 기반으로 value function 업데이트
  • 업데이트된 value function을 바탕으로 새로운 게임 진행, 더 많이 실행할수록 에이전트가 더욱 잘 학습

Temporal Difference Learning

• 각 타임스텝마다 value function 업데이트
  • 전체 reward의 합인 G_t를 알 수 없기 때문에, R_t+1과 다음 상태의 할인값 V(S_t+1)을 더함으로써 G_t를 측정 (=TD target)
  • 더 많은 스텝을 진행할수록 에이전트가 더욱 잘 학습

Q-Learning

Q-learning이란

• off-policy
• value-based method
  • 각 상태(state) 혹은 상태-행동(state-action) 쌍의 값(value)을 나타내는 value function 혹은 action-value function을 학습함으로써 최적의 policy를 간접적으로 학습하는 방법
  • Q-learning의 경우 action-value function인 Q-function을 학습
• TD approach (Temporal Difference Learning)
  • 에피소드가 끝날 때가 아니라 각 단계마다 action-value function을 업데이트
• Q = Quality (value) of that action at that state

value, reward, and Q-table

• value
  • 어떤 상태, 혹은 상태-행동 쌍의 값(value)이란 해당 상태(혹은 상태-행동 쌍)에서 시작해 policy에 따라 행동함으로써 얻는 기대누적보상(expected cumulative reward)을 의미
• reward
  • 특정 상태에서 어떠한 행동을 취한 이후 환경으로부터 얻는 feedback
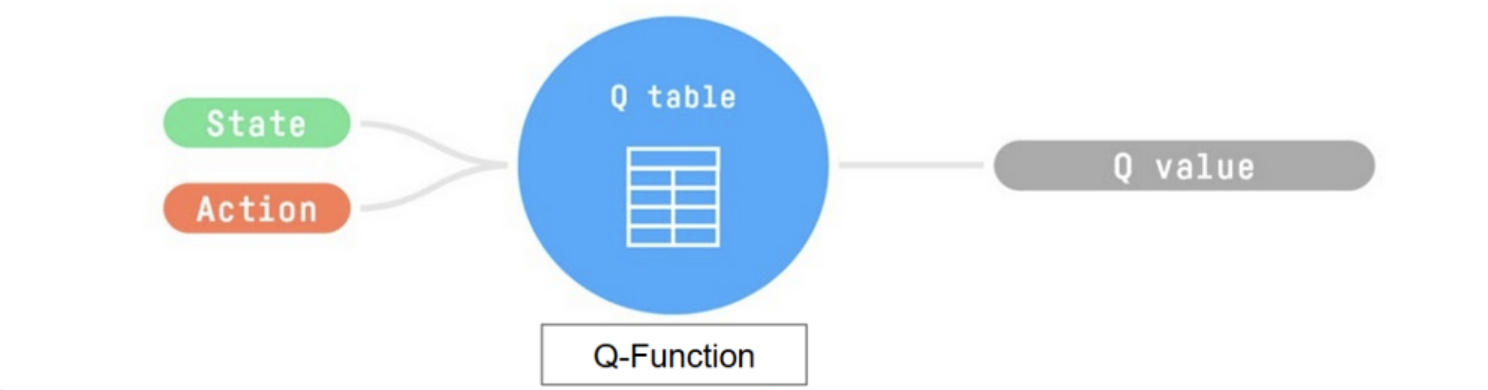
• Q-table
  • state-action 쌍의 값(value)에 상응하는 셀을 가진 테이블(표)
  • Q-function을 위한 메모리로 생각할 수 있음
  • 최적의 Q-function을 얻는다는 것은 최적의 Q-table을 얻는다는 것과 동일하며, 각 상태에서 어떤 행동을 취하는 것이 최선임을 안다는 것이기 때문에 최적의 policy를 가진다고 볼 수 있음
  • 처음에 Q-table은 임의의 값으로 초기화되어 있기 때문에 환경을 탐색하면서 Q-table을 업데이트함에 따라 최적의 policy에 더욱 가까운 근사값을 얻을 수 있음

Q-learning algorithm

Step 1. Q-table 초기화

• 각 state-action 쌍에 대해 Q-table 초기화 (일반적으로 0)

Step 2. epsilon-greedy 전략을 이용해 action 선택

• epsilon-greedy 전략은 exploration/exploitation trade-off를 처리할 수 있는 Policy
  • (epsilon) 확률만큼 exploration (임의의 행동) 수행
  • (1-epsilon) 확률만큼 exploitation (가장 높은 state-action 값을 가지는 행동) 수행
• 초기에는 epsilon을 높게 설정해 대부분 explore를 수행하고, Q-table이 점차 좋아짐에 따라 epsilon 값을 감소시켜 exploitation의 비중을 늘림

Step 3. action 수행 후 다음 reward와 다음 state 관찰

Step 4. Q(state, action) 업데이트

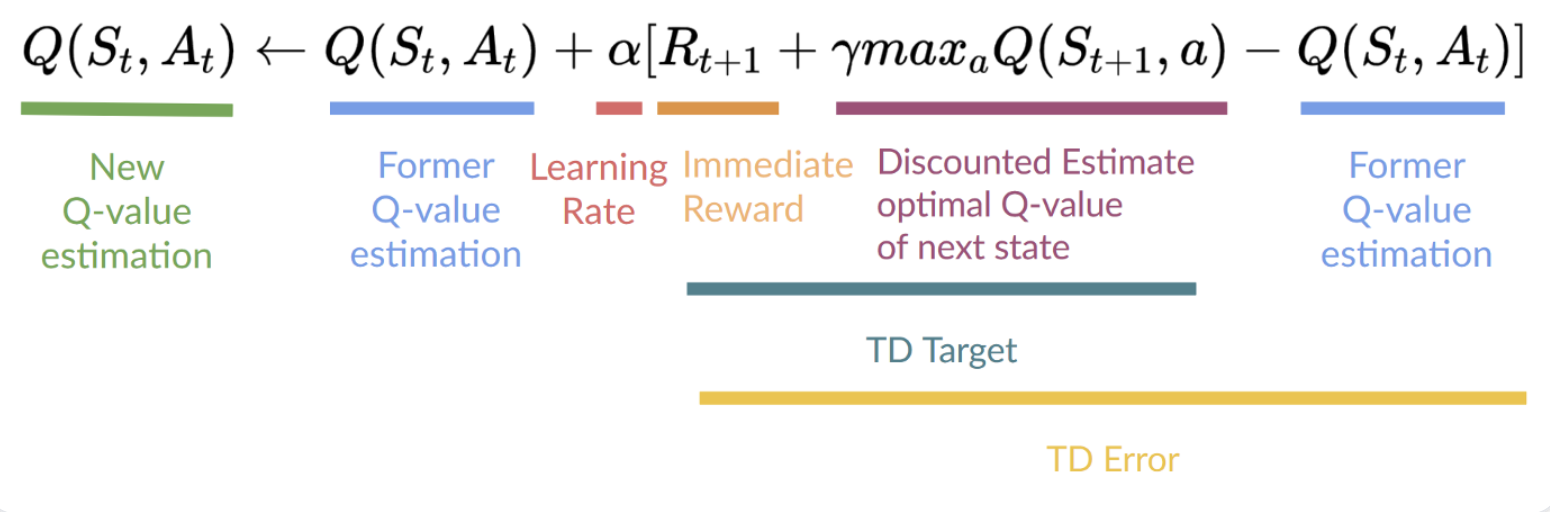
• TD learning을 따르기 때문에 각 단계(step)마다 value function을 업데이트
• 즉각적인 보상(reward) R_t+1과 다음 상태(state)의 최적의 할인값 rV(S_t+1)을 더해 target으로 사용
  • TD target에서 최고의 next-state-action 쌍의 값을 얻기 위해서 greedy policy 사용 (언제나 가장 높은 값을 가지는 state-action을 선택)
• Q-value를 업데이트한 뒤 epsilon-greedy policy를 사용해 다음 상태에서 행동을 선택

Off-policy, On-policy

• off-policy
  • 행동(추론)과 업데이트(학습)에 다른 policy를 사용
  • Q-learning의 경우, acting policy인 epsilon-greedy policy와 Q-value를 업데이트하기 위해(updating policy) 최고의 next-state-action 값을 찾을 때 사용되는 greedy policy는 구분됨
• on-policy
  • 행동과 업데이트에 동일한 policy 사용