참고 링크: https://huggingface.co/learn/deep-rl-course/unit4/introduction?fw=pt
강화학습
- 누적 리워드(reward) 기댓값을 최대화하는 최적의 policy를 찾는 것이 목표
Value-based

- 최적의 policy를 찾기 위한 중간 단계로 value function을 측정하는 방식
- value function을 학습
- 최적의 value function이 최적의 policy로 이어진다는 아이디어에서 출발
- 실제 action-value function을 근사하기 위해 예측값과 타겟값 사이의 loss를 최소화
- policy는 action value를 측정하기 위한 단순한 함수 (e.g. greedy-policy)
- value function으로부터 직접적으로 생성됨
- value-based deep reinforcement learning
- 어떤 상태(state)에서 가능한 행동(action)에 대한 각기 다른 Q-value를 근사하기 위해 deep neural network를 사용
Policy-based

- 최적의 policy를 직접 학습
- value function을 학습하지 않음
- policy를 파라미터화 (parameterized)
- e.g. policy를 neural network로 표현해 action에 대한 확률분포를 생성
- gradient descent를 활용해 파라미터로 표현된 policy의 성능을 최대화
- objective function(=cumulative reward)을 최대화할 수 있는 파라미터 theta를 찾고자 함
Policy-based vs. Policy-gradient
- policy-gradient는 policy-based의 부분집합
- policy-based method에서 최적화는 대부분 on-policy
- 가장 최근 버전의 policy에 의해 수집된 데이터를 활용해 업데이트
- policy-based, policy-gradient는 모두 최적의 policy를 직접 찾는 방식
- policy-based method에서 최적화는 대부분 on-policy
- policy-based는 파라미터를 간접적으로 최적화
- e.g. hill climbing, simulated annealing, evolution strategy, ...
- policy-gradient는 파라미터를 직접적으로 최적화
- e.g. gradient ascent
Policy-gradient
장점
- 추가적인 데이터(=action value)를 저장할 필요 없이 policy를 직접 측정
- stochastic(=확률적) policy 학습 가능
- value function은 불가능
- quasi-deterministic policy (e.g. greedy epsilon)
- exploration/exploitation trade-off를 사람이 직접 구현할 필요가 없음
- perceptual aliasing(=두 state가 동일해보이나 다른 action을 필요로 하는 경우)의 문제가 사라짐
- 확률적으로 action이 결정되기 때문
- value function은 불가능
- 고차원의 action space나 연속적인 action space에 효과적
- value-based의 경우 가능한 모든 action에 대해 Q-value를 리턴해야 하며, 그 중 최대값을 가진 action을 고르는 것은 복잡한 최적화 문제가 됨
- policy-gradient는 action에 대한 확률분포를 리턴하면 됨
- 수렴(convergence)이 용이
- value-based는 Q-estimate에서 최대값을 취함으로써 value function을 변화시킴
- 측정된 action value의 작은 변화에도 action을 취할 확률이 급격하게 변할 수 있음
- 반면 policy-gradient에서 action을 선택할 가능성은 시간이 지남에 따라 부드럽게 변화
- value-based는 Q-estimate에서 최대값을 취함으로써 value function을 변화시킴
단점
- global optimum이 아니라 local optimum으로 수렴하는 경우가 많음
- 학습 시 시간이 오래 걸림 (step by step)
- variance가 높음
기본 개념
- policy gradient
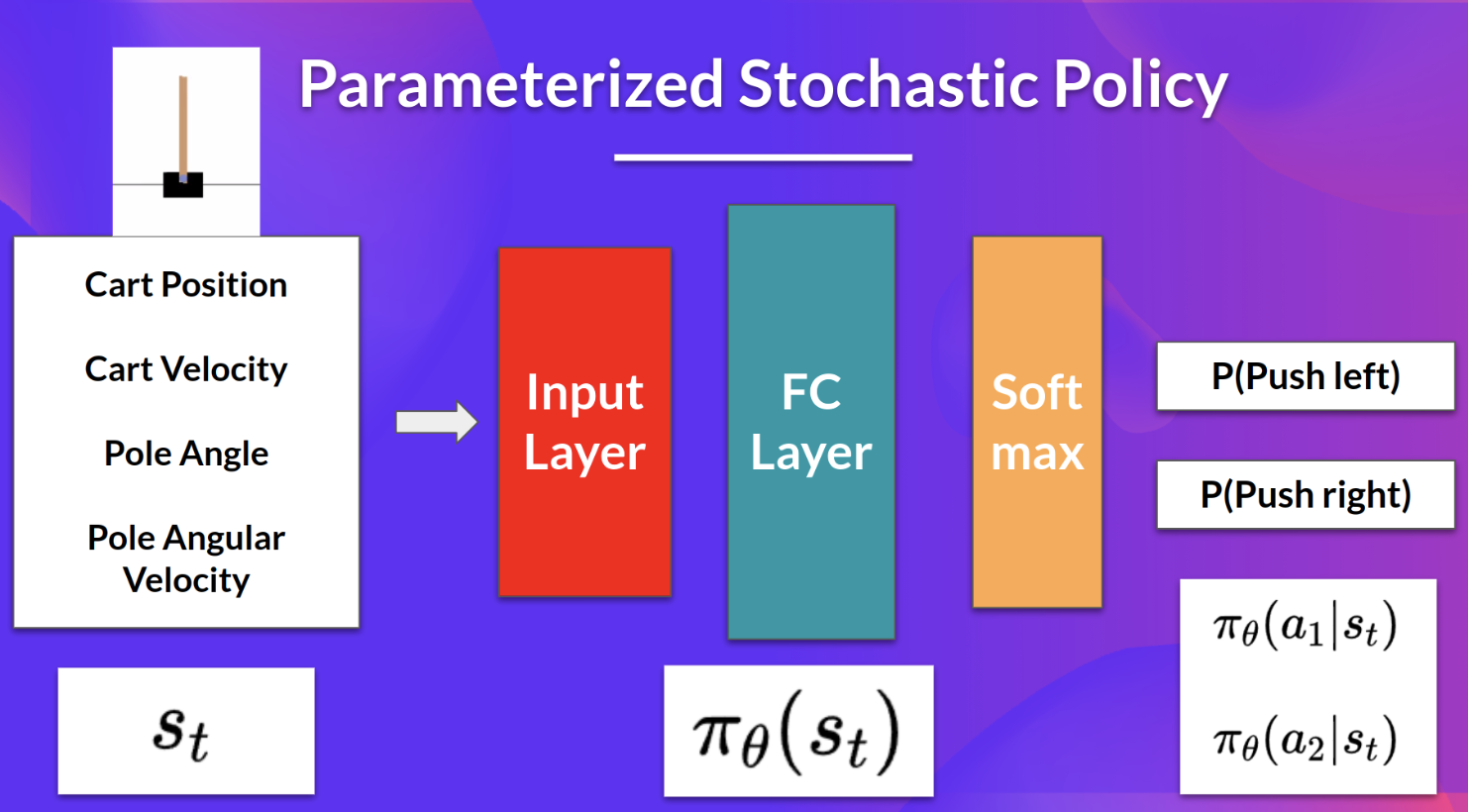
- 기댓값을 최대화하기 위한 파라미터를 찾는 방법
- 파라미터를 가진 확률적 policy를 가정 (parameterized stochastic policy)
- 리턴을 최대화하는 좋은 action이 미래에 더욱 자주 샘플링되도록 policy를 튜닝

- 기댓값을 최대화하기 위한 파라미터를 찾는 방법
- action preference
- 각 action을 취할 확률
- stochastic policy
- 파라미터 theta를 가진 policy π를 가정
- state가 주어지면 action에 대한 확률분포를 output으로 리턴

목적함수 (objective function)
- 어떠한 policy가 좋은 것인지 측정하기 위한 방법
- trajectory(=state action sequence)가 주어지면 누적 리워드의 기댓값을 결과로 리턴
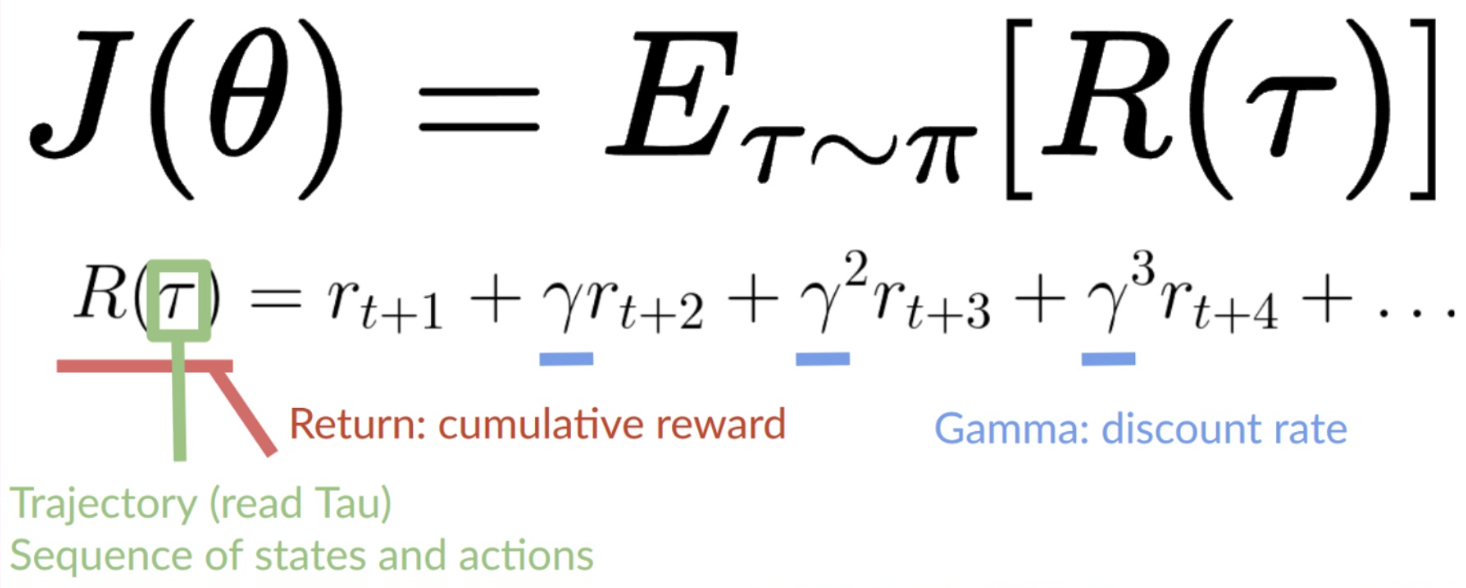
- 기댓값은 [임의의 trajectory의 누적 리워드 X 해당 trajectory의 확률을 곱한 값]의 전체합으로 표현 가능
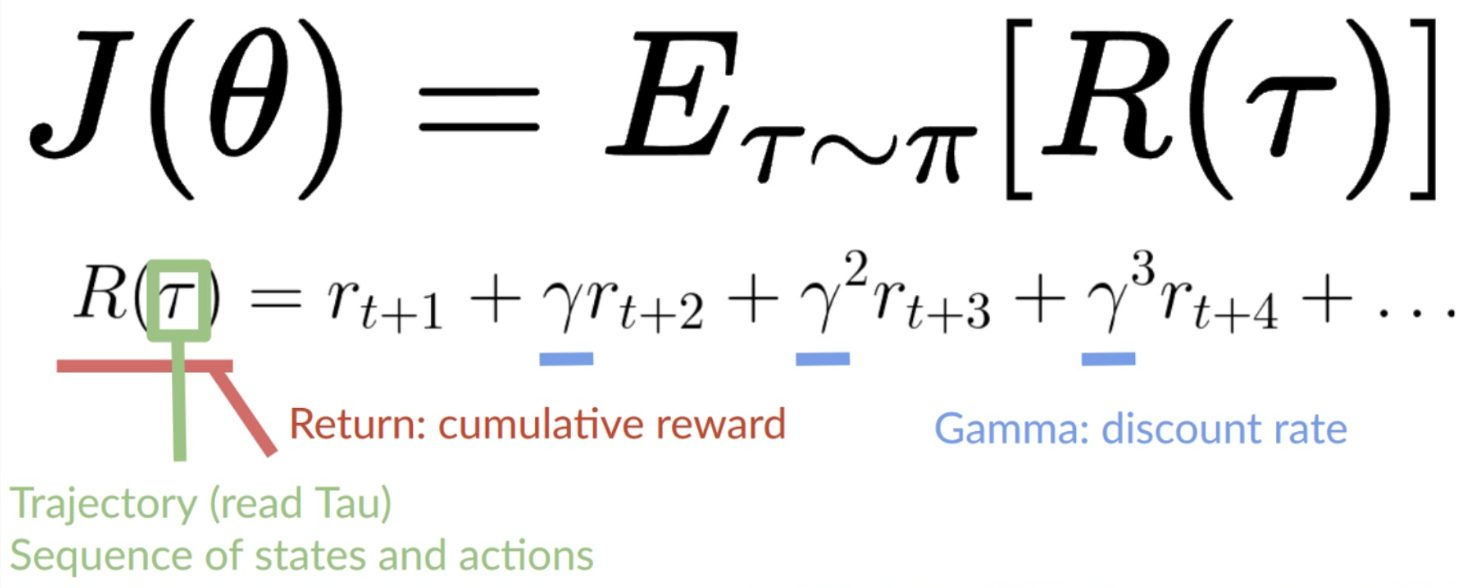
- trajectory의 확률 P는 특정 timestep t에서 state, action이 주어졌을 때 다음 state가 나올 확률(=state distribution)과 해당 timestep t에서 특정 action을 취할 확률로 표현할 수 있음
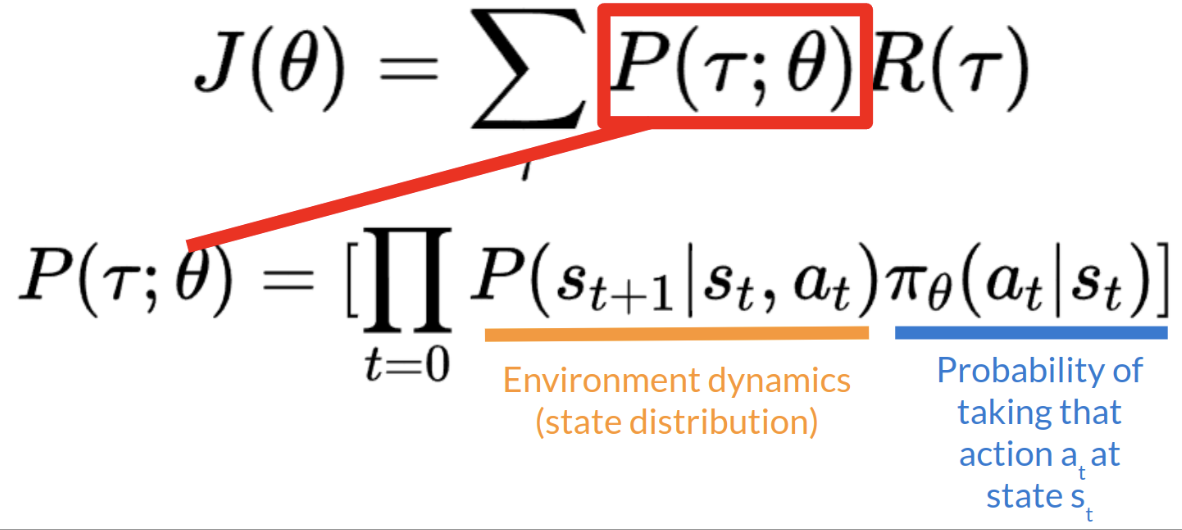
- 우리의 목표는 objective function J를 최대화하는 weight(=parameter) theta를 찾는 것
gradient ascent
- 목적함수 J를 최대화하는 theta를 찾고자하기 때문에 gradient-ascent 필요
- gradient-descent와는 반대로, 기울기가 가장 가파른 증가를 보이는 방향으로 파라미터 학습
- θ←θ+α∗∇θJ(θ)
- J 미분 계산의 어려움
- 가능한 모든 trajectory의 확률을 계산하는 것은 많은 연산을 요구 (expensive)
- 몇 개의 trajectory를 모아 계산하는 sample-based 측정으로 gradient estimation 진행
- 목적함수를 미분하기 위해서는 state distribution (=Markov Decision Process dynamics)를 미분해야 하는데, 이를 모르기 때문에 미분이 어려움
- policy gradient theorem을 활용해 목적함수를 state distribution의 미분이 필요하지 않은 형태로 재구성
- policy gradient theorem 설명 링크 (link)
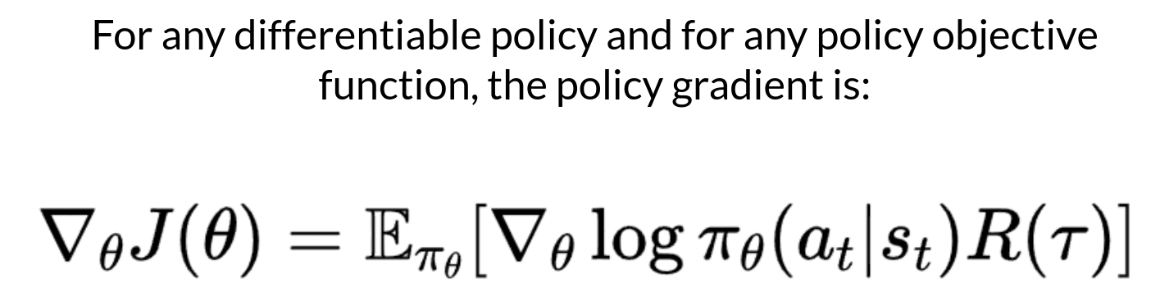
- 가능한 모든 trajectory의 확률을 계산하는 것은 많은 연산을 요구 (expensive)
Reinforce 알고리즘 (Monte Carlo Reinforce)
- policy 파라미터를 업데이트하기 위해 전체 에피소드로부터 측정된 리턴값을 사용하는 policy-gradient 알고리즘
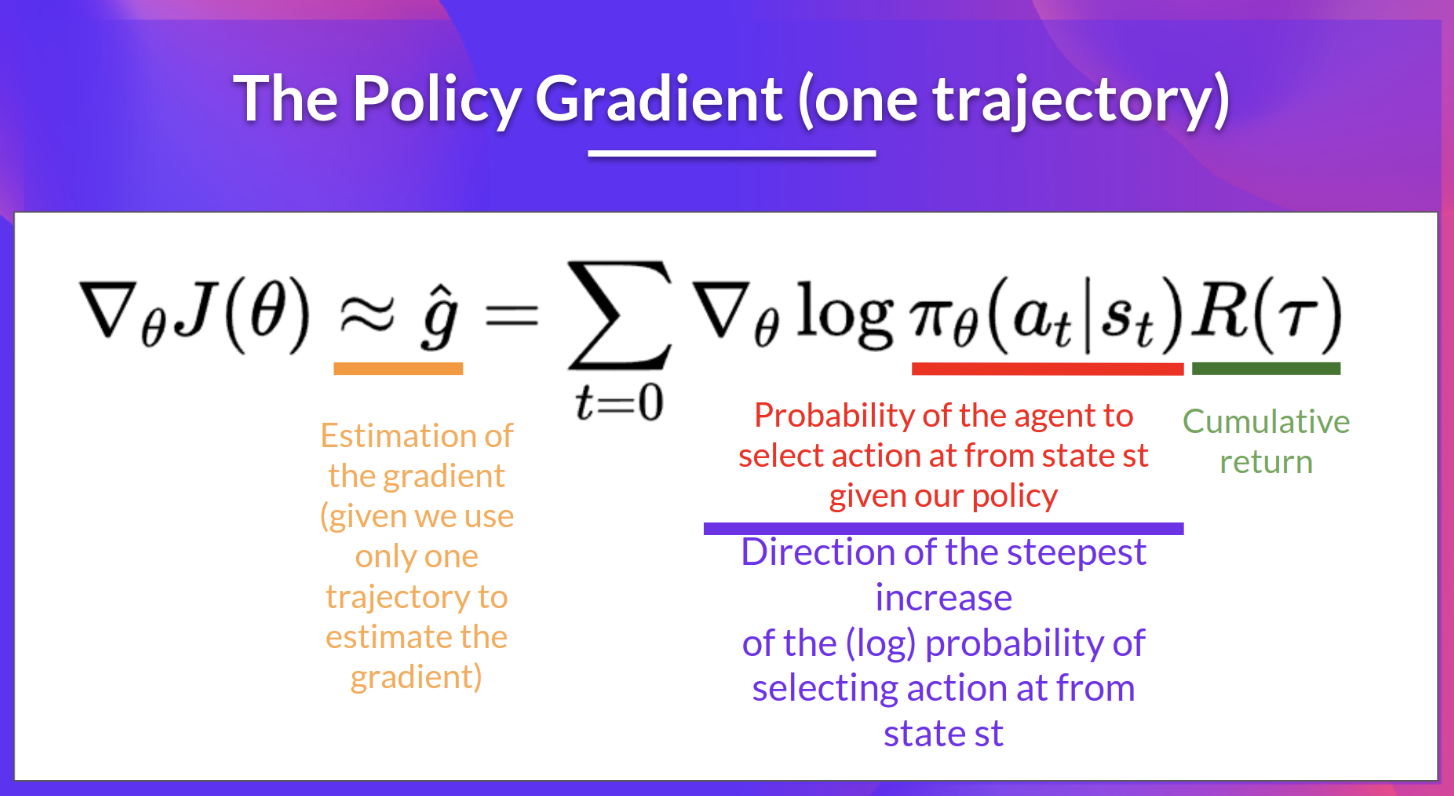
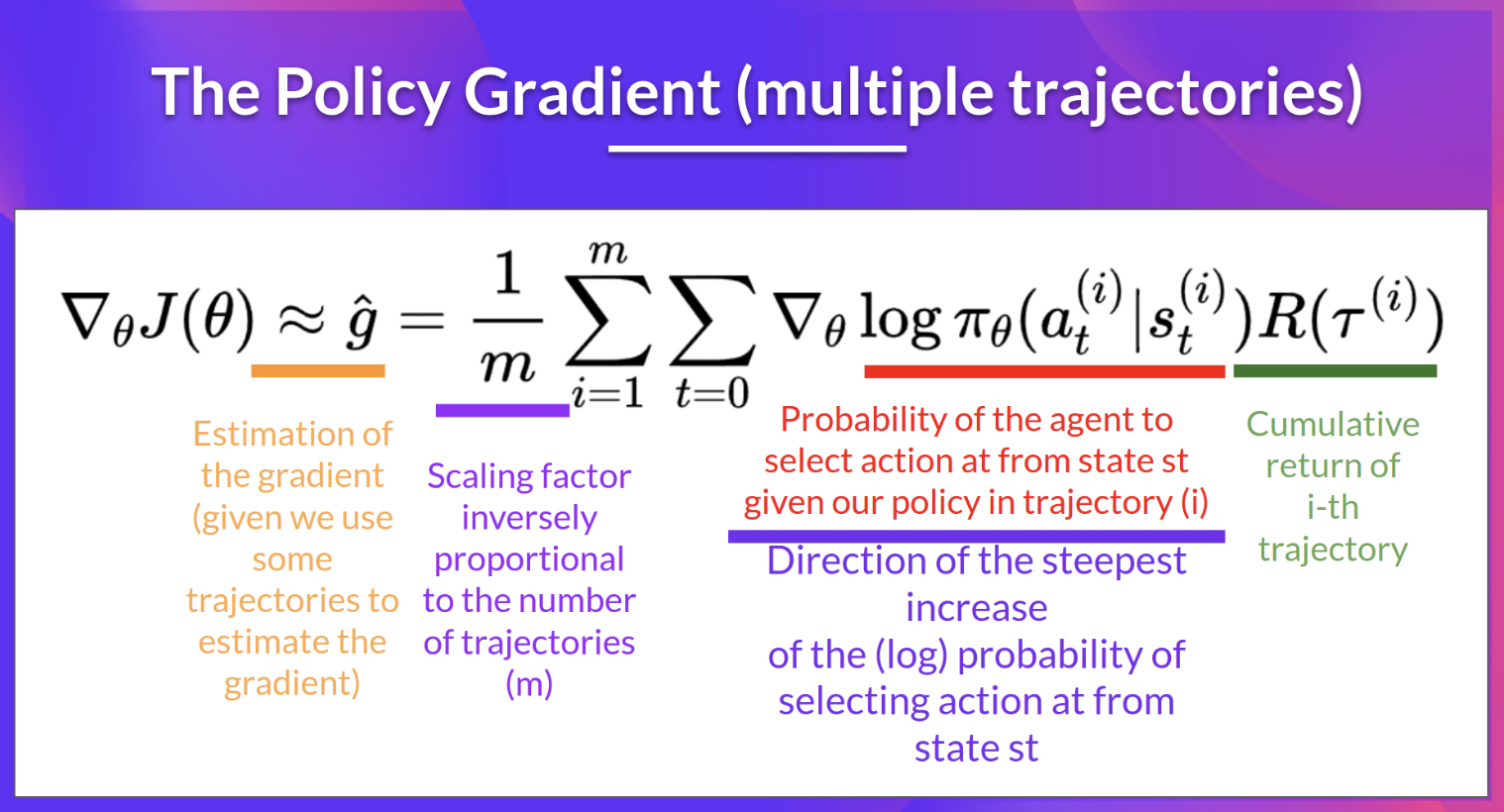
- 위 그림의 보라색 부분은 state t에서 action을 선택하는 확률의 가장 가파른 증가 방향을 나타냄
- 즉, 확률을 높이거나 낮추기 위해 policy의 weight을 어떻게 바꿀 수 있는지를 알 수 있음
- 위 그림의 초록색 부분은 점수 함수
- 리턴값이 높다면 (state, action) 조합의 확률을 높임
- 위 그림의 보라색 부분은 state t에서 action을 선택하는 확률의 가장 가파른 증가 방향을 나타냄