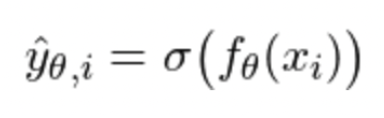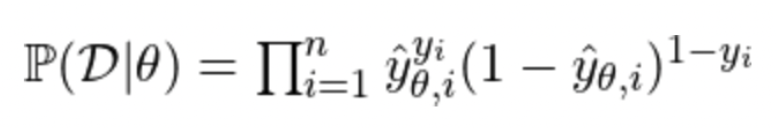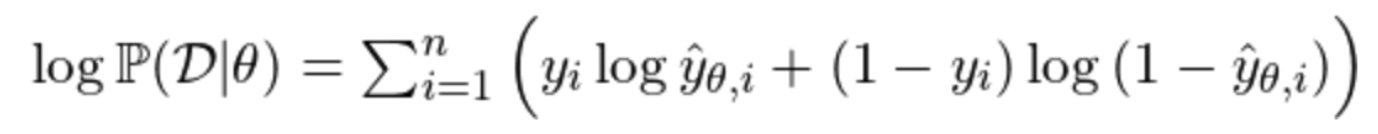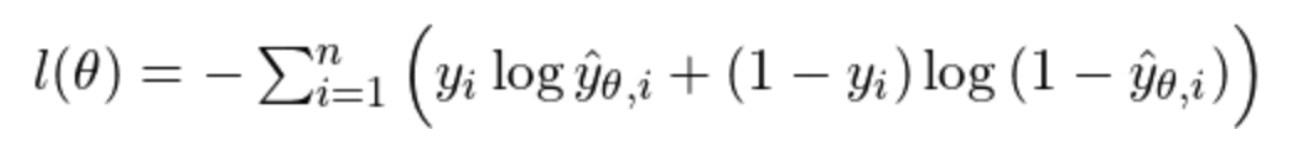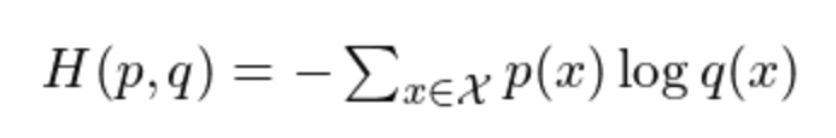Log Probability, Negative Log Likelihood and Cross-Entropy 설명

Log Probability를 사용하는 이유

• 일반적인 확률의 범위는 [0, 1]이며, 이를 log probability로 변형할 시에 (-무한대, 0]이 됨
• log probability는 산술(arithmetic)적인 차원에서 다음과 같은 이점을 지님
  • Stability
    • 일반적인 확률을 곱하는 등의 연산을 수행하다보면 0과 가까운 값을 가지게 됨
    • 이는 한정적인 정확도 근사치(finite precision approximation)에서는 불안정
  • Simplification
    • 확률 혹은 확률밀도(probability density)에서 로그를 취하는 것은 특정 연산을 단순화하는 데에 도움을 줌
    • 예를 들어 density의 gradient를 구할 때 (특히 density가 exponential family에 속해있을 경우)

Negative Log Likelihood

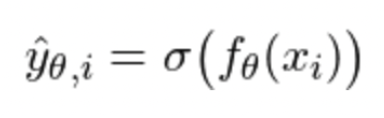
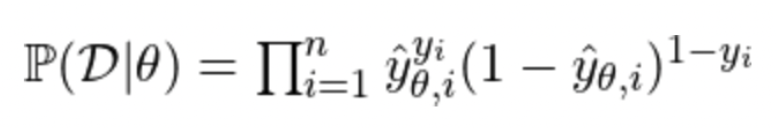
• Maximum Likelihood Estimation
  • 주어진 x를 input으로 받는 모델 f가 가장 true label과 일치하는 예측값 y_hat을 만들도록 하는 theta(weight, 가중치)를 찾는 것이 우리의 목표
    • 시그마는 non-linear activation (비선형 활성화 함수)
    • 이러한 비선형 활성화 함수는 값을 (-inf, inf)에서 [0, 1]로 매핑
    • 이를 위해 우리는 true label과 prediction이 일치하도록 주어진 확률(likelihood)을 최대화해야 함

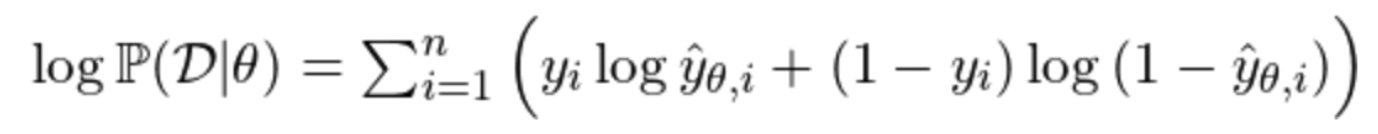
• Log-Likelihood
  • 예측 성능이 얼마나 좋은지 판단하기 위해 확률을 볼 때, log를 활용하면 곱을 합으로 바꿔주는 등 arithmetic 이점이 존재
  • 위의 수식은 binary classifcation을 가정한 것으로, y_hat은 i번째 데이터가 긍정, 1-y_hat은 i번째 데이터가 부정일 확률을 나타냄
  • 실제 label과 연관된 log probability를 더해주는 방식으로 log-likelihood를 구할 수 있음

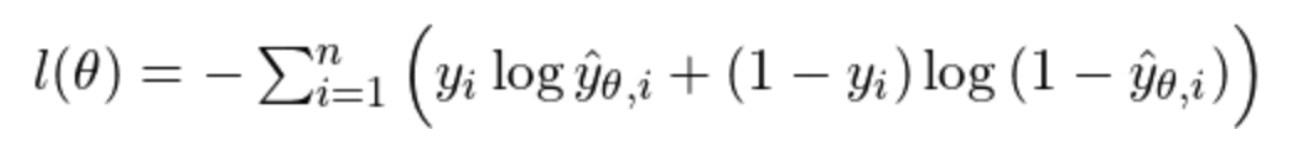
• Minimizing Negative Log-Likelihood
  • 우리는 손실(loss), 즉 정답과 예측값 사이의 오차를 '최소화'하는 방향으로 학습을 진행해야 함
  • 위에서 설명한 Maximum Likelihood Estimaion 대신 -를 붙여 Negative Log-Likelihood Loss를 구할 수 있음
    • NLL = proxy problem to find solution for MLE

Cross-Entropy Loss

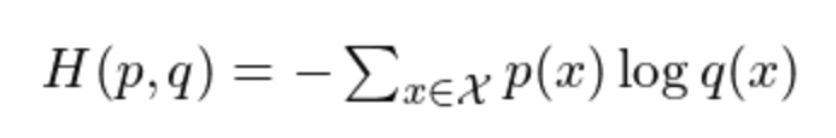
• NLL과 CE의 정의는 동일
• 하지만 둘은 Pytorch에서는 다르게 구현되어 있음
  • CrossEntropyLoss의 구현은 내부적으로 softmax activation 이후 log transformation을 적용하나 NLLLoss는 그렇지 않음
  • CrossEntropyLoss는 raw prediction vaue를 기대하는 반면 NLLLoss는 log probability를 기대

More about Cross-Entorpy Loss

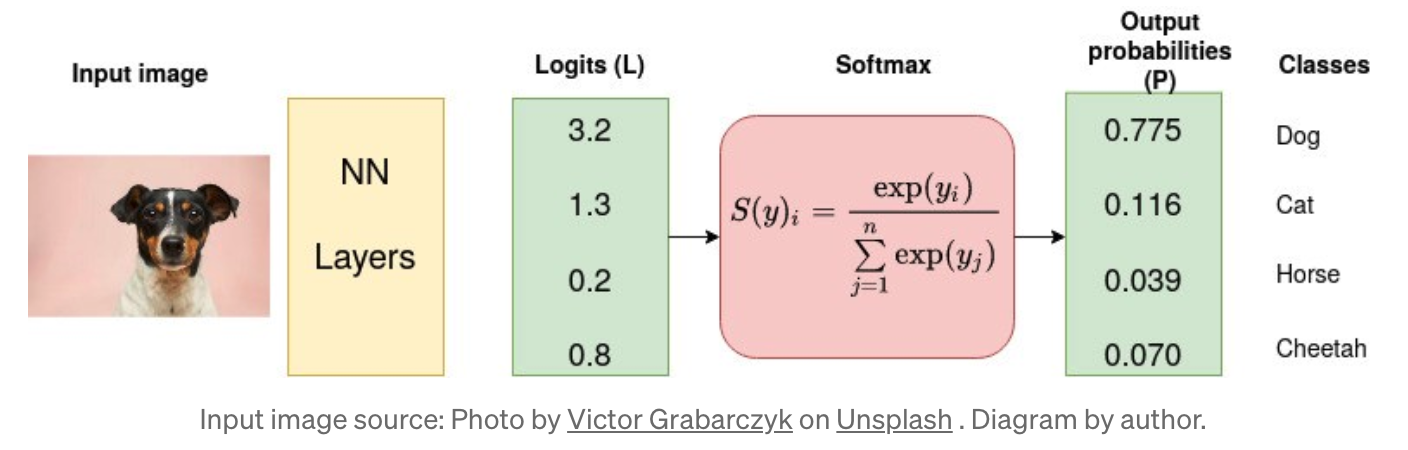
• Cross-Entropy Loss
  • Softmax를 통해 logits을 output probability로 변환하고, 이러한 확률과 실제 값(true value) 사이의 거리를 측정하는 것이 Cross-Entropy의 목적
  • 예측값과 실제값과의 차이가 적어지도록 모델의 가중치(weight)를 반복적으로 조정하는 것이 바로 모델을 학습하는 것

• 엔트로피란, 내재된 불확실성을 측정하는 것으로, 크면 클수록 확률분포의 불확실성이 커지며 작을수록 불확실성이 작아짐
• CE Loss는 logarithmic loss, log loss, logistic loss라고 불리기도 함
• Categorical Cross-Entropy vs. Sparse Categorical Cross-Entropy
  • 둘다 multi-label classification에 적용될 수 있다는 점에서 유사점을 가짐
  • sparse categorical의 경우 실제 정답(label)이 정수로 되어 있음
  • categorical은 실제 정답이 one-hot encoding 형태로 구성되어 있음

관련 링크: (link1, link2, link3)