Variational Autoencoder (차원축소, Autoencoder, Reparameterization trick)

Variational Autoencoders (VAE)

• VAE는 GAN과 함께 생성모델(deep generative model)의 한 축을 이룸
• 간단히 설명하자면, 새로운 데이터를 생성하기 좋은 특성들을 갖는 latent space를 보장하도록 학습 중에 인코딩 분포를 정규화(regularized)하는 오토인코더(autoencoder)의 일종
• variational(변화의)이라는 용어는 정규화(regularization)와 통계학의 변분추론(variational inference) 사이에 긴밀한 연관관계가 있기 때문

Dimensionality Reduction (차원 축소)

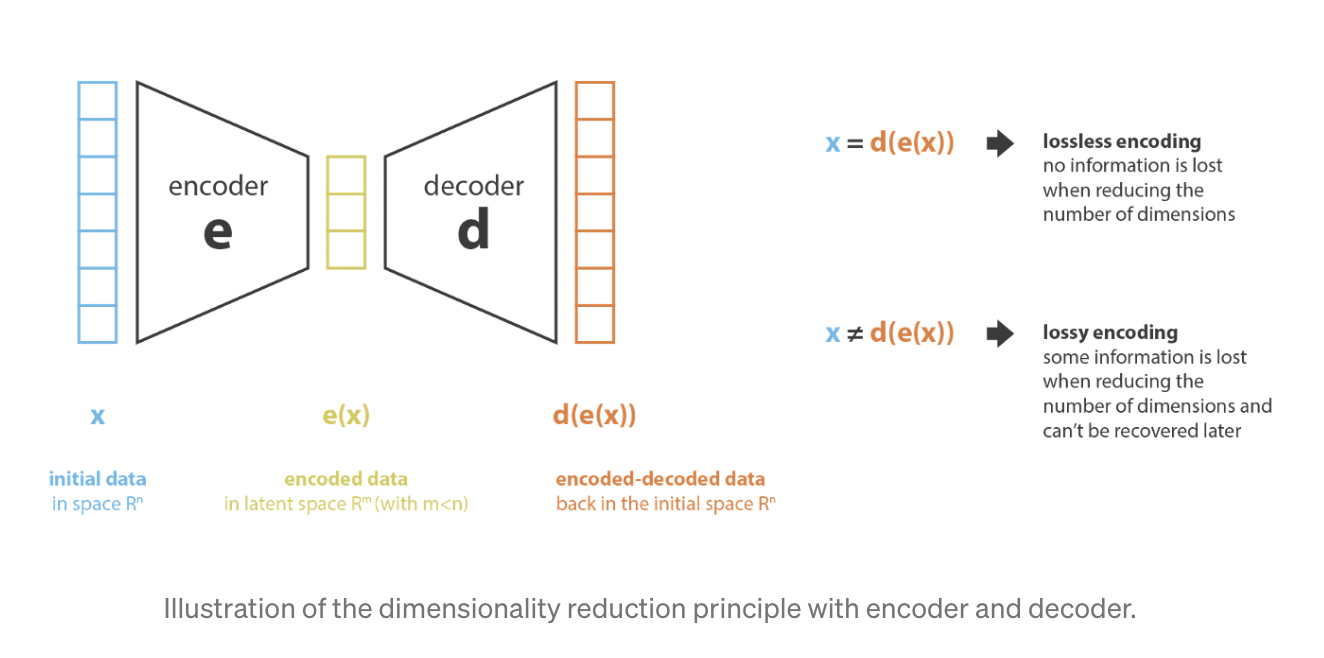
• 머신러닝에서 차원축소란, 데이터를 묘사하는 피처(특징)의 개수를 줄이는 과정
• 예전 feature representation으로부터 새로운 feature representation을 만드는 과정을 수행하는 부분을 인코더, 반대의 과정을 수행하는 부분을 디코더라고 부를 수 있음
  • 차원축소는 인코더가 데이터를 압축하는 과정(즉, encoded space = latent space로 압축)으로 이해 가능
• 차원축소의 주요한 목표는 인코딩 시에 정보를 최대한으로 보존하고, 디코딩 시에 재건 오류(reconstruction error)를 최소화

Principal Components Analysis (PCA)

• 차원축소의 한 방법
• 예전 피처들의 선형결합인 새로운 독립적인 피처들을 만들어, 새로운 피처들로 정의된 projections of the data on the subspace가 처음의 데이터들과 가능한 한 가깝도록 (euclidean distance)
• 다시 말해, PCA는 초기 space의 best linear subspace를 찾아 오차값이 가능한 작도록 만드는 방법
• eigenvalue / eigenvector problem

Autoencoder

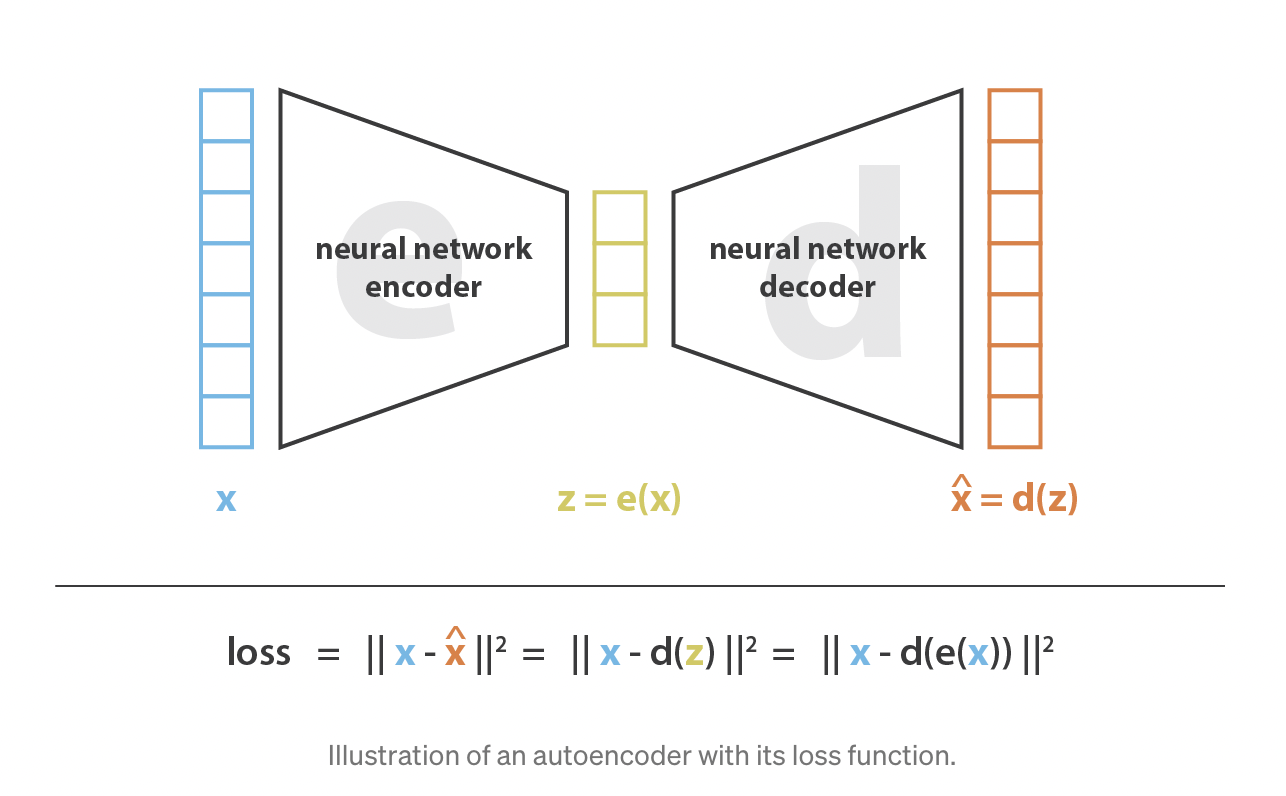
• 인코더와 디코더를 신경망(neural network)으로 만들고 반복적인 최적화 과정을 통해 최적의 인코딩-디코딩 스킴을 학습
• 만약 인코더, 디코더 아키텍처가 비선형성 없이 오직 하나의 층(layer)을 갖고 있다면, 우리가 gradient descent로 구할 수 있는 여러 최적의 해 중 하나가 PCA로 얻을 수 있는 해라고 이해할 수 있음 (link between linear autoencoder and PCA)
• 인코더와 디코더가 deep and non-linear라면, 아키텍처가 복잡할수록 reconstruction loss를 낮게 유지하면서도 더 높은 차원축소를 진행할 수 있음
  • 단, 이럴 경우 latent space의 해석가능 구조 결여(lack of regularity)가 발생할 수 있다는 점과 차원축소의 최종 목표는 축소된 representation에 주요한 정보를 유지해야 한다는 점을 염두에 두어야

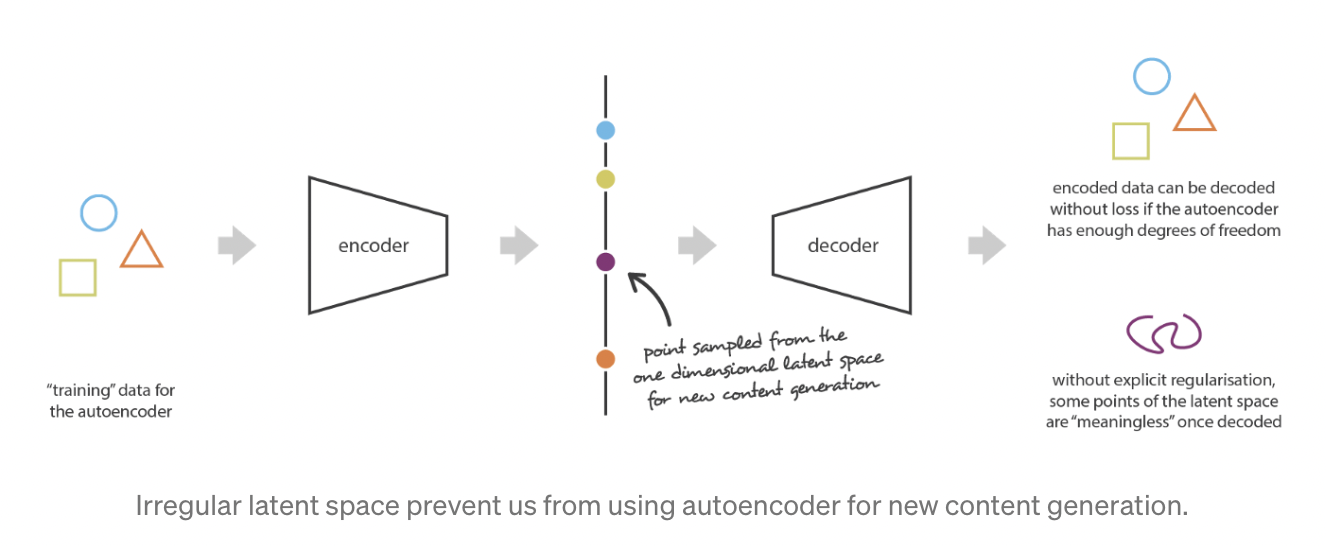
• Autoencoder는 latent space가 얼마나 잘 조직화(organized)되었는지와 관계없이 최소한의 loss를 갖는 방향으로 인코딩과 디코딩을 할 수 있도록 학습되었음
  • 때문에 새로운 컨텐츠를 생성해내기 어려움

Variational Autoencoder

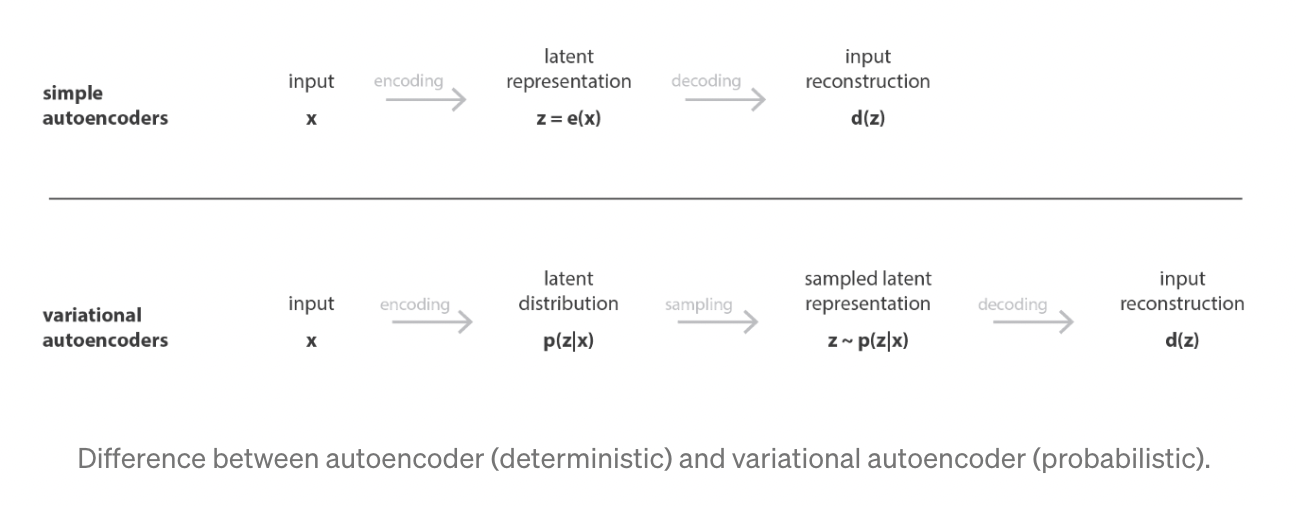
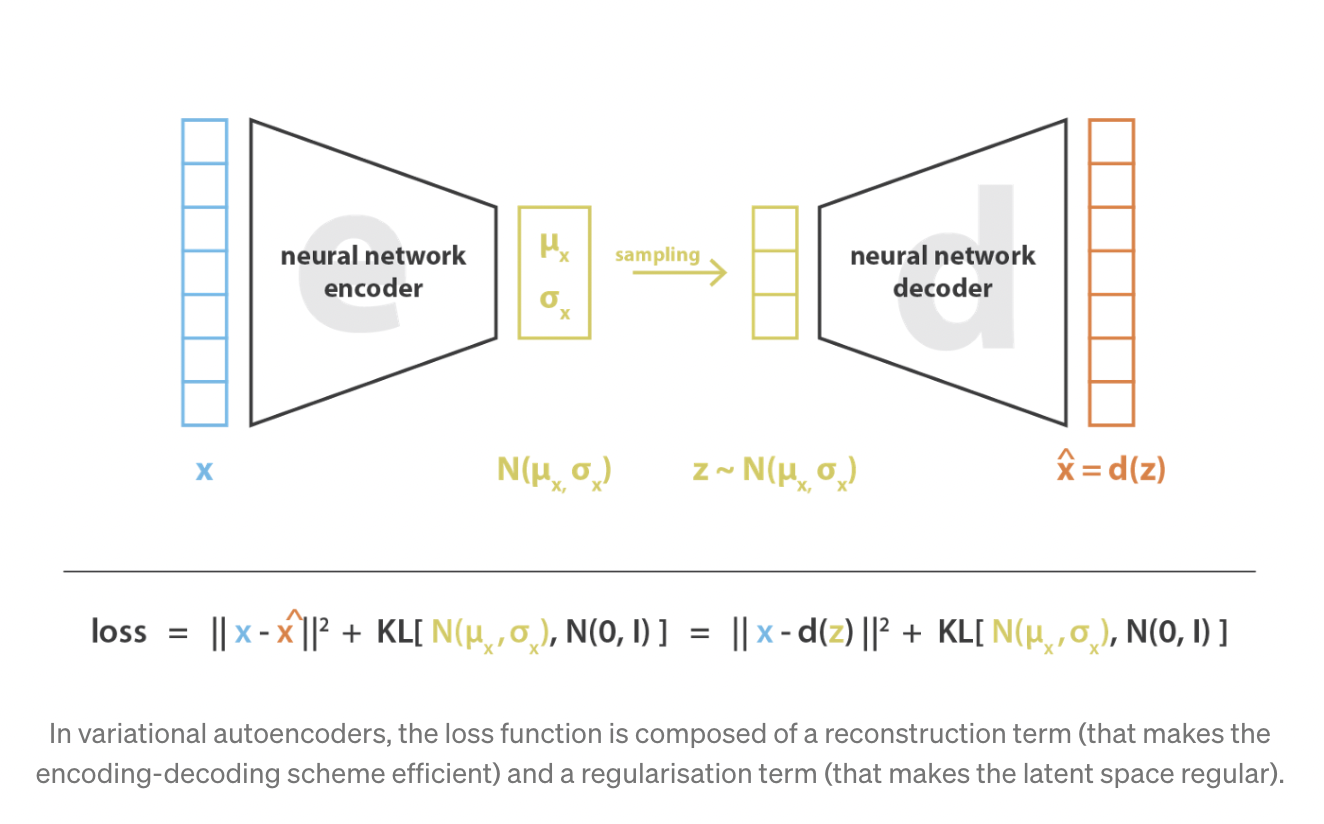
• 오토인코더가 생성의 목표를 달성하기 위해서는 latent space가 충분히 regular해야 함
  • 이를 위해 학습과정에서 explicit regularization을 적용할 수 있음
  • a variational autoencoder can be defined as being an autoencoder whose training is regularised to avoid overfitting and ensure that the latent space has good properties that enable generative process
• regularization을 적용하기 위해 input을 하나의 점으로 인코딩하는 대신 latent space 상의 분포(distribution)로 인코딩
• 여기서의 regularization이란, continuity와 completeness 만족
  • continuity: latent space에서 가까이 위치한 두 점은 디코딩되었을 때 완전히 다른 컨텐츠를 제공해서는 안 됨
  • completeness: 선택된 분포에 대해서, latent space로부터 샘플링된 점은 디코딩되었을 때 의미있는 컨텐츠를 제공해야 함

Reparameterization trick

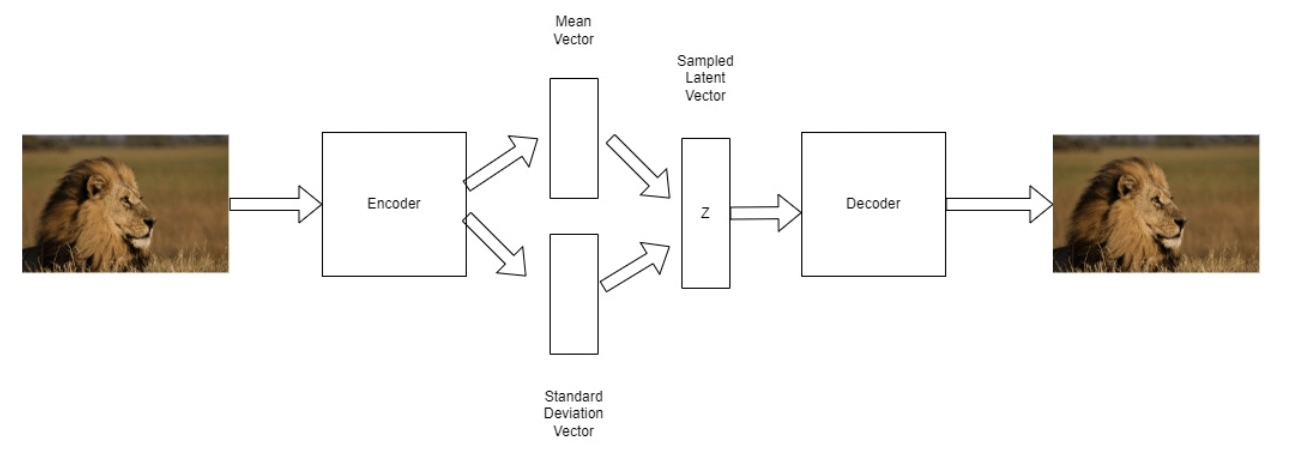
• 일반적인(vanilla) autoencoder의 경우 embedding space에 불연속성을 갖고 있기 때문에 좋은 생성 샘플을 만들어낼 수 없음
  • 하지만 VAE는 더욱 연속적인 embedding space를 만들어냄으로써 기존의 autoencoder를 개선
• VAE는 가우시안 분포의 파라미터를 학습하는데, 인코더는 분포의 평균과 표준편차라는 두 개의 벡터를 예측하도록 학습
  • 하지만, 모델에 의해 파라미터화된 분포로부터 샘플링하는 과정은 미분불가능하다는 문제 존재
• 이를 해결하기 위해 사용하는 것이 reparameterization trick
  • 이는 가우시안 샘플링을 파라미터화하는 방법의 시행을 다르게 하는 것을 의미
  • 즉, 랜덤 샘플링을 noise term으로 취급
  • 이를 통해 stochastic smapling operation에 묶여있지 않고 모델의 파라미터를 미분가능하도록 바꿔줄 수 있음 (reparameterization allows a gradient path through a non-stochastic node)

관련 링크 (link1, link2)