[Algorithm] 다이나믹 프로그래밍

kiteB·2022년 3월 25일

DP algorithm dynamic programming python 다이나믹 프로그래밍

Algorithm-Python

목록 보기

6/7

[ 다이나믹 프로그래밍이란? ]

큰 문제를 작게 나누고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결하는 알고리즘 기법으로, 동적 계획법으로 불리기도 한다.

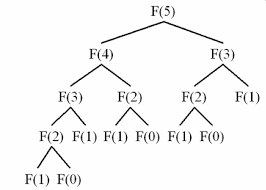
1. 다이나믹 프로그래밍의 조건

DP 알고리즘을 적용하기 위해서는 다음 2가지 조건을 만족해야 한다.

Overlapping Subproblem

Optimal Substructure

✅ Overlapping Subproblem (중복되는 부분 문제)

주어진 문제가 여러 개의 부분 문제(subproblem)로 쪼개질 수 있는 것을 말한다.

대표적인 예로 피보나치 수열이 있다. 피보나치 수열은 첫째 항과 둘째 항이 1이며, 그 뒤에 모든 항이 바로 앞 두 항의 합인 수열을 말한다.

N번째 피보나치 수를 구할 때, (N - 2)번째 피보나치 수 구하기 + (N - 1)번째 피보나치 수 구하기로 작은 문제로 나눌 수 있다.

✅ Optimal Substructure (최적 부분 구조)

새로운 부분 문제의 정답을 다른 부분 문제의 정답으로부터 구할 수 있는 것을 말한다.

앞에서 언급한 피보나치 수열을 구할 때, 8번째 피보나치 수를 구하면서 구했던 4번째 피보나치 수와 9번째 피보나치 수를 구하면서 구했던 4번째 피보나치 수는 항상 같다.

즉 매번 4번째 피보나치 수를 구하지 않고, 전에 구했던 값을 기억해서 사용할 수 있다.

2. 다이나믹 프로그래밍의 접근 방법

다이나믹 프로그래밍의 접근 방법에는 Top-Down과 Bottom-Up가 있다.

✅ Top-Down

Top-Down 방식의 특징
- 재귀 함수를 이용하여 다이나믹 프로그래밍 소스코드를 작성하는 방법을 큰 문제를 해결하기 위해 작은 문제를 호출한다고 해서 Top-Down(탑-다운)이라고 한다.
- 하향식이라고도 한다.
- 메모이제이션은 탑다운 방식에 국한되어 사용되는 표현이다.
  - 엄밀히 말하면 메모이제이션은 이전에 계산된 결과를 일시적으로 기록해 놓는 넓은 개념을 의미하므로, 다이나믹 프로그래밍과는 별도의 개념이다.
- python의 경우 재귀 함수의 스택 크기가 한정되어 있을 수 있기 때문에 Bottom-Up 방식으로 구현하는 것이 좋다.
  - sys 라이브러리에 포함되어 있는 setrecursionlimit() 함수를 호출하여 재귀 제한을 완화할 수 있다.
Top-Down 방식으로 문제를 푸는 방식
1. 문제를 작은 문제로 나눈다.
2. 작은 문제들을 푼다.
3. 작은 문제들의 답으로 전체 문제를 푼다.
피보나치 수열 (Top-Down 방식)

d = [0] * 100


def fibo(x):
    print('f(' + str(x) + ')', end=' ')
    if x == 1 or x == 2:
        return 1
    if d[x] != 0:
        return d[x]
    d[x] = fibo(x - 1) + fibo(x - 2)
    return d[x]


fibo(6)

✅ Bottom-Up

Bottom-Up 방식의 특징
- 단순히 반복문을 이용하여 소스코드를 작성하는 경우 작은 문제부터 차근차근 답을 도출한다고 하여 Bottom-Up(보텀업) 방식이라고 한다.
- 상향식이라고도 한다.
- 다이나믹 프로그래밍의 전형적인 형태로, 보텀업 방식에서 사용되는 결과 저장용 리스트는 DP 테이블이라고 부른다.
Bottom-Up 방식으로 문제를 푸는 방식
1. 가장 작은 문제부터 푼다.
2. 문제의 크기를 점점 크게 만들어서 전체 문제를 푼다.
피보나치 수열 (Bottom-Up 방식)

d = [0] * 100

d[1] = d[2] = 1
n = 99

for i in range(3, n + 1):
    d[i] = d[i - 1] + d[i - 2]

print(d[n])

[ 다이나믹 프로그래밍 vs 분할 정복 ]

큰 문제를 작은 문제로 나눈다는 측면에서 분할 정복 알고리즘과 비슷하게 느껴지지만 다음과 같은 차이점이 존재한다.

분할 정복은 분할했을 경우 반복적인 문제가 발생하지 않지만, DP는 반복적인 문제가 발생하기 때문에 메모이제이션(Memoization)기법들이 필요하게 됩니다.
이 과정에서 DP는 별도의 메모리를 소비하기 때문에 그리디 알고리즘에 비해 시간 복잡도는 크지만 문제를 풀 수 있는 스펙트럼이 넓고 근삿값이 아닌 최적의 값을 얻을 수 있습니다.