1.3.1 Continuous-Time Sinusoidal Signals

eggmo·2024년 4월 13일
DSP디지털 신호 처리

DSP

목록 보기
10/10

연속시간에서 정현파(Sinusoidal) 함수는 아래와 같다.

xa(t)=Acos⁡(Ωt+θ)−∞<t<∞[1.3.1]x_a(t) = A \cos(\Omega t + \theta) \quad -\infty < t < \infty \quad\quad\quad\quad\quad\quad [1.3.1]
Ω=각주파수\Omega = 각주파수 \quad\quad\quad\quad\quad\quad\quad\quad
t=시간t = 시간 \quad\quad\quad\quad\quad\quad\quad\quad\quad
θ=위상\theta = 위상 \quad\quad\quad\quad\quad\quad\quad\quad\quad

여기서 각주파수의 의미를 잘 파악해야 한다. Ω\Omega 는 정현파 함수가 얼마나 빨리 회전하는지를 의미한다.

이해가 안가면 아래의 [그림 1] 을 참고 해보자.

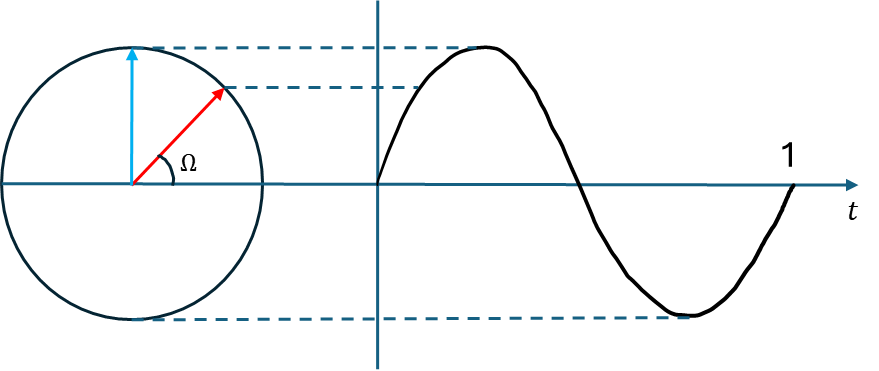
                                      [그림 1]



만약 Ω\Omega 가 2π2\pi 라고 가정해보자. 이 뜻은 왼쪽 원에서 화살표가 1초에 2π2\pi 라디안 (360도)를 회전한다는 의미이다.

[그림 1]의 왼쪽 원 화살표의 높이를 점선으로 이어보면 [그림 1]의 오른쪽과 같은 정현파 함수가 그려진다.

오른쪽 정현파 함수를 보면 사인(Sine)함수의 파형을 나타내는데 주기가 1초이고 주파수는 1Hz 임을 확인할 수 있다.


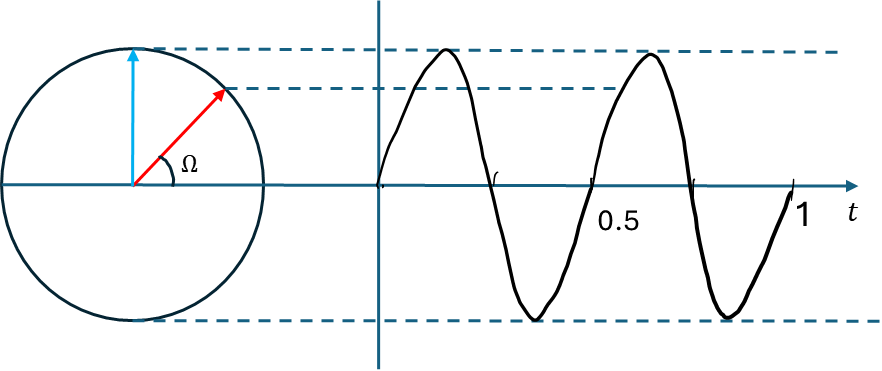
                                      [그림 2]


만약 Ω\Omega가 4π4\pi 라고 가정해보자 이 뜻은 왼쪽 원에서 화살표가 1초에 4π4\pi 라디안 (720도) 를 회전한다는 의미이다. [그림 2]의 오른쪽 정현파 함수를 보면 사인 함수의 파형의 주기는 0.5초이고 주파수는 2Hz 임을 확인 할 수 있다.

여기서 Ω\Omega 와 정현파 함수의 주기 TT, 주파수 FF의 관계를 확인 할 수 있다.

Ω=2πF=2πT[1.3.2]\Omega = 2\pi F = \frac{2\pi}{T} \quad\quad\quad [1.3.2]

즉 주파수 FF가 1이면 정현파 함수는 1초에 2π2\pi의 각속도로 진동(회전)하고 주파수 FF가 2이면 정현파 함수는 1초에 4π4\pi의 각속도로 진동(회전)한다.

수식 (1.3.1)과 수식(1.3.2)를 조합하면 수식 (1.3.3)이 완성된다.

xa(t)=Acos⁡(2πFt+θ)−∞<t<∞[1.3.3]x_a(t) = A \cos(2\pi Ft + \theta) \quad -\infty < t < \infty \quad\quad\quad\quad\quad\quad [1.3.3]


수식 (1.3.3)으로 표현되는 정현파 함수는 [그림 2]에서와 같이 주기성(periodic)을 가진다. 주기성을 가지는 신호를 주기 신호(Periodic Signal)라고 한다. 연속 시간 정현파 신호는 아래 3가지 특성을 가진다.

첫번째. 연속 시간 정현파 신호를 주기의 정수배만큼 x축으로 평행 이동 해도 동일한 파형을 나타낸다.

수식으로 표현하면 (1.3.3.1)과 같다.

xa(t+Tp)=xa(t)[1.3.3.1]x_a(t+T_p) = x_a(t) \quad \quad\quad\quad\quad[1.3.3.1]


TpT_p는 기본 주기(fundamental period)라고 정의 한다. 기본 주기는 절대값이 가장 작은 주기를 의미한다.

예를 들어 [그림 2]에서 주기는 0.5이다. 이 신호는 x축으로 0.5의 정수배만큼 평행 이동 시켜도 동일한 모양을 유지한다.

이때 절댓값이 가장 작은 0.5가 신호의 기본 주기가 된다.


두 번째. 연속 시간 정현파 신호는 기본 주기 TpT_p가 다르면 그 자체로 유일하다.

쉽게 풀어말하면 기본 주기가 1인 정현파 신호와 기본 주기가 2인 정현파 신호는 서로 다른 유일한 신호라는 뜻이다.

이는 연속 시간 정현파 신호의 중요한 특성이다. 다른 의미로는 기본 주기의 범위는 1 ~ ∞\infty 까지 가능하고 이 범위 내에서 기본 주기를 가지는

연속 시간 정현파 신호는 모두 다른 신호이다.


세 번째. 정현파 신호의 주파수 FF가 커지면 신호의 진동수가 많아진다.

[그림 1]과 [그림 2]에서 확인할 수 있듯이 주파수가 커질수록 1초동안 진동하는 횟수가 많아진다.


수식 (1.3.1)은 실수 평면(Cartesian 좌표계)에서 표현되었다. 하지만 수식의 편의성을 위해 복소 평면에서 연속 신호 정현파 신호를 표기할 수 있다.

xa(t)=Aej(Ωt+θ)[1.3.4]x_a(t) = Ae^{j(\Omega t + \theta)} \quad\quad\quad\quad [1.3.4]
e±jθ=cosθ ±sin⁡θ[1.3.5]e^{\pm j\theta} = cos\theta \ \pm \sin\theta \quad\quad\quad[1.3.5]
xa(t)=Acos(Ωt +θ)=A2ej(Ωt+θ) +A2e−j(Ωt+θ)[1.3.6]x_a(t) = Acos(\Omega t \ + \theta) = \frac{A}{2}e^{j(\Omega t + \theta)} \ + \frac{A}{2}e^{-j(\Omega t + \theta)} \quad\quad\quad\quad [1.3.6]


수식 (1.3.1)은 오일러 공식 (1.3.4) , (1.3.5)를 활용해 (1,3,6)으로 표현 가능하다.

(1.3.6)의 우항에서 표현되는 A2ej(Ωt+θ)\frac{A}{2}e^{j(\Omega t + \theta)} 와 A2e−j(Ωt+θ)\frac{A}{2}e^{-j(\Omega t + \theta)}는 서로 켤례 복소수(Complex-Conjugate) 관계이다. 이를 복소 평면에서 나타내보면

[그림 3]이다.

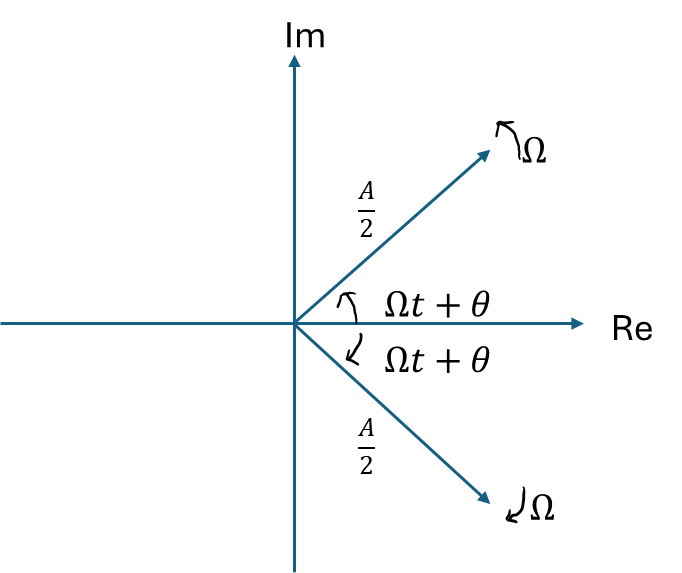
                                     [그림 3]


A2ej(Ωt+θ)\frac{A}{2}e^{j(\Omega t + \theta)} 는 [그림 3]의 위쪽 화살표(벡터)를 의미하고 반시계 방향으로 회전한다.

반대로 A2e−j(Ωt+θ)\frac{A}{2}e^{-j(\Omega t + \theta)} 는 [그림 3]의 아래쪽 화살표(벡터)를 의미하고 시계 방향으로 회전한다.

즉 Cos함수는 진폭 AA의 절반의 크기를 가지고 각주파수가 Ω\Omega인 벡터와 진폭 AA의 절반의 크기를 가지고 각주파수가 −Ω-\Omega인 벡터로 표현이 가능하다.

profile
eggmo
안녕하세요eggmo입니다.
이전 포스트

1.3.2 Discrete-Time Sinusoidal Signals

0개의 댓글