1.3.2 Discrete-Time Sinusoidal Signals

이산 시간 정현파 신호 (Discrete-Time-Sinusoidal-Singal)은 수식 [1.3.7] 같이 표현 가능하다.

연속 시간 신호에서 각주파수는 $\Omega$로 표현했지만 구분을 위해 이산 시간 신호에서 각주파수는 $\omega$로 표현한다.

이산 시간에서 각주파수는 [1.3.8] 과 같이 표현한다.

수식 [1.3.8]이 이해가 가지 않는다면 포스팅 1.3.1 Continuous-Time Sinusoidal Signals에 자세히 설명되어 있다.

수식 [1.3.7]에 수식 [1.3.8]을 대입하면 수식 [1.3.9]가 만들어진다.

각주파수와 마찬가지로 연속 시간 신호에서 주파수는 $F$로 표현했지만 구분을 위해 이산 시간 신호에서 주파수는 $f$로 표현한다.

이산 시간 신호의 각주파수 $w$는 연속 시간 신호의 각주파수 $\Omega$와 차이를 보인다. 설명을 위해 [그림 1]을 참고 해보자.

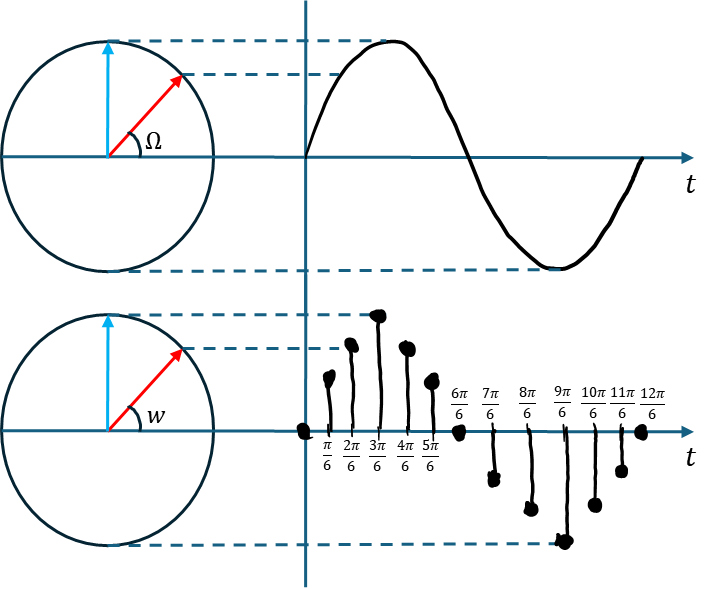
                                      [그림 1]

[그림 1]의 위쪽 신호는 연속 시간 정현파 신호이고 [그림 1]의 아래쪽 신호는 이산 시간 정현파 신호이다.

연속 시간 정현파 신호의 각 주파수 $\Omega$는 1초당 진동(회전)하는 라디안이므로 단위가 radian/sec 이다. [그림 1]에서 $\Omega$는 $2\pi$이다.

반면 이산 시간 정현파 신호의 각 주파수 $w$ 는 1초 동안 샘플링된 데이터당 진동(회전)하는 라디안이므로 단위가 radian/sample 이다.

[그림 1]에서 이산 시간 정현파 신호는 1초 동안 12번의 샘플링이 일어났고 주기는 12 Samples 이다. 따라서 이산 시간 정현파 신호의 각 주파수 $w$는 $\frac{\pi}{6}$ 이다.


이산 시간 정현파 신호는 3가지 특성을 가지고 있다.

첫번째. 이산 시간 정현파 신호의 각주파수는 유리수(Rational Numbe)로 표현 된다. 명확한 증명은 아래와 같다.


이산 시간 정현파 신호는 연속 시간 정현파 신호와 동일하게 주기 신호(Periodic Signal)이다. 주기 신호는 식 [1.3.10] 처럼 표현 가능하다.

이산 시간 신호는 시간이 양수 일 때 부터 연속 시간 신호를 샘플링하기 때문에 $n$ > 0 이다. 따라서 이산 시간 신호의 주기 $N$ 도 0보다 크다.

주기 신호이기 때문에 주기 $N$의 정수배 만큼 시간축에서 평행이동 하면 동일한 파형이 나온다. 수식 [1.3.10]을 만족하는 주기 $N$의 후보 중 절댓값이 가장 작은 주기를 기본 주기(Fundamental Periodic)이라고 한다. 그리고 기본 주기의 역수를 기본 주파수라고 한다.


예를 들어 기본 주파수가 $f_0$ 인 이산 시간 정현파 신호가 있다고 가정하자. 이 신호는 주기 신호이기 때문에 식 [1.3.10]을 식 [1.3.9]에 대입하여 식 [1.3.10.1]로 표현할 수 있다.

식 [1.3.10.1]을 잘 살펴보면 괄호 안에 $2\pi f_0N$ 이 없어진 것을 확인할 수 있다. 즉 cos 함수 내에서 아무역할을 할 수 없는 것이다.

$cos(2k\pi+\theta)$ 는 $cos\theta$ 로 표현할 수 있다. 결국 $2\pi f_0N$는 $2k\pi$로 표현이 가능하기 때문에 생략이 된 것이다.

$2\pi f_0N = 2k\pi$ 이기 때문에 식 [1.3.11]이 유도된다.

따라서 이산 시간 정현파 신호의 주파수 $f_0$는 유리수 이며 $k$와 $N$이 서로소(Relatively Prime)일 때 분모 $N$이 이산 시간 정현파 신호의 주기가 된다. 그리고 $\frac{1}{N}$이 이산 시간 정현파 신호의 기본 주파수가 된다.


두번째. 이산 시간 정현파 신호의 주파수가 $2\pi$가 차이나는 서로 다른 이산 시간 정현파 신호는 동일하다.

여기서 각 주파수 $w_k$를 가지고 $w_k = w_0 + 2k\pi$를 만족하는 이산 시간 정현파 신호가 있다고 가정하면 아래와 같이 표현이 가능하다.

즉 $w_0 = w_k$이다. 결국 $Acos(w_kn+\theta)$와 $Acos(w_0n+\theta)$가 동일한 이산 시간 신호 정현파 이다.

결국 이산 시간 정현파 신호는 각 주파수가 $2\pi$ 인 범위 내에서 모든 신호를 표현할 수 있다. 따라서 이산 시간 정현파 신호의 각 주파수를

$-\pi <= w <= \pi$ 의 $2\pi$ 범위로 제한할 수 있다. (왜 0 <= $w$ <= $2\pi$ 로 안했냐고 묻는다면 정확히는 모른다... 수식 전개를 쉽게 하려고 한 듯..)

이 특성은 연속 시간 정현파 신호와 큰 차이를 보인다. 연속 시간 정현파 신호는 모든 각 주파수에 대해서

유일한 신호를 가졌다면 이산 시간 정현파 신호는 $-\pi <= w <= \pi$ 범위 내에서 유일한 신호를 가진다.

$-\pi>w$ , $w > \pi$ 인 범위에서 이산 시간 정현파 신호는 $-\pi <= w <= \pi$ 의 신호와 동일한 신호가 존재하게 된다. 이해가 안되면 그림 2를 참조하자

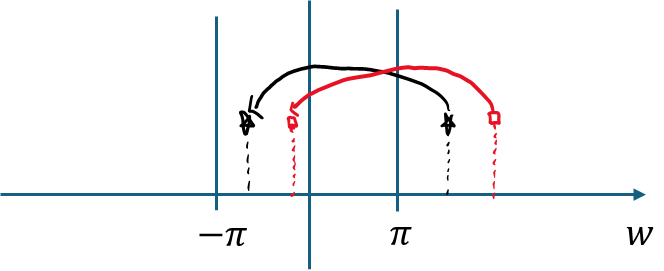
                                      [그림 2]

[그림 2]에서 별 위치에 있는 $w$값은 $w-2\pi$ 위치인 별과 동일한 신호이고 네모 위치에 있는 $w$역시 $w-2\pi$ 위치의 네모와 동일한 신호인 것이다.

이러한 현상을 간섭(alias)라고 한다.

연속 시간 정현파 신호의 각주파수는 모든 실수 범위에서 유일하기 때문에 간섭(alias)가 발생하지 않는다.


세번째. $w = \pi$ 일 때 이산 시간 정현파 신호는 가장 빠르게 진동한다.

당연한 말이다. 각 주파수가 클수록 정현파 신호는 가장 빠르게 진동한다. 이산 시간 각 주파수의 범위는 $-\pi <= w <= \pi$ 이므로 $w=\pi$에서 가장 큰 값이다.