Knowledge Distillation에서 Temperature의 영향

Monotonic growth·2024년 8월 7일

Deep Learning Knowledge distillation machine learning

정의

가장 기본적인 Knowledge Distillation의 수식은 다음과 같은 Softened Softmax Function으로 정의되고, 이를 Hinton’s Knowledge Distillation이라고 한다.

q_i = \frac{e^{z_i / \tau}}{\sum_{j \in U} e^{z_j / \tau}} \qquad \text{(Softed Softmax Function)}

Temperature Hyperparameter $\tau$ 의 역할

$\tau$ 가 커진다 → 각 확률 $q_i$ 간의 차이가 줄어든다. (Why?)
따라서, Student Model은 Teacher 모델이 간과했던 정보를 다시금 생각하게 된다.
해당 정보를 Dark Knowledge라고 한다.

Analysis

$z_i$ 는 전체 $|U|$ 가지의 값이 가능하다. 따라서 $q_i$ 의 증감 추세를 식으로 파악하기에는 쉽지 않다.
이에 다음 두 가지 방법을 제안한다. $q_i$ 를 $\tau$ 에 대한 함수값 $q_i(\tau)$ 로 생각할 수 있다.

Method1. Derivative

각 항에 대한 Partial derivative를 구해본다.

\begin{aligned}\frac{\partial q_i}{\partial \tau} &= \frac{-z_i \cdot \exp\left(\frac{z_i}{\tau}\right) \cdot \sum_j \exp\left(\frac{z_j}{\tau}\right) + \exp\left(\frac{z_i}{\tau}\right) \cdot \sum_j z_j \cdot \exp\left(\frac{z_j}{\tau}\right)}{\tau^2 \left(\sum_j \exp\left(\frac{z_j}{\tau}\right)\right)^2} \\ &= \frac{ \exp\left(\frac{z_i}{\tau}\right) \left( \sum_j (z_j-z_i) \cdot \exp\left(\frac{z_j}{\tau}\right)\right)}{\tau^2 \left(\sum_j \exp\left(\frac{z_j}{\tau}\right)\right)^2} \end{aligned}

$z_i > z_j$ 인 경우가 Dominant : $\frac{\partial q_i}{\partial \tau} < 0$
$z_i < z_j$ 인 경우가 Dominant : $\frac{\partial q_i}{\partial \tau} > 0$

따라서, 확률 값의 차이를 줄이는 방향으로 움직인다.

Method2. Limit

\lim_{\tau \to \infin} q_i = \frac{1}{n}

임은 자명하다.

즉, 온도를 무한히 올렸을 경우 모든 인덱스가 가지는 확률이 동일해진다.

$q_i < \frac{1}{n}$ : $q_i$ 증가 추세 (i.e. Not Monotone)
$q_i < \frac{1}{n}$ : $q_i$ 감소 추세 (i.e. Not Monotone)

따라서, 원래 값의 차이를 줄이는 방향으로 움직인다.

Experiment

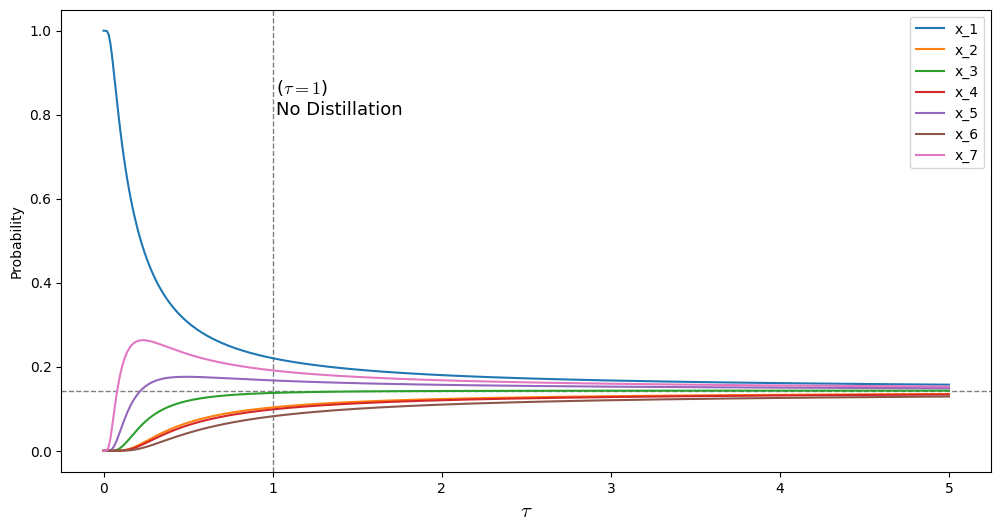
아래의 코드를 이용해서 간단히 실험해볼 수 있다. 실제로 $\tau$ 가 커질 수록 모든 확률이 $\frac{1}{n}$ 으로 수렴하는 것을 알 수 있다.

import numpy as np
import random as rd
import matplotlib.pyplot as plt


def softmax(x):
    exp_x = np.exp(x - np.max(x))
    sum_exp_x = np.sum(exp_x)
    return exp_x / sum_exp_x
    
    
def knowledge_distillation(x: np.array, t: float):
    if t == 0:
        t = 1e-10
    return softmax(x / t)
    
    
def experiment(x_dim: int, min_t: int, max_t: int):
    x = np.random.rand(x_dim)
    T = np.linspace(min_t, max_t, (max_t - min_t) * 100)
    y_T = np.array([knowledge_distillation(x, t) for t in T])

    plt.figure(figsize=(12, 6))
    plt.rcParams['mathtext.fontset'] = 'cm'
    plt.axhline(1/x_dim, min_t, max_t, color='gray', linestyle='--', linewidth=1)
    plt.axvline(1, min_t, max_t, color='gray', linestyle='--', linewidth=1)
    plt.text(1.02, 0.8, r'($\tau=1$)' + '\nNo Distillation', fontdict={'fontsize':13})
    plt.xlabel(r'$\tau$', fontdict={'fontsize':15})
    plt.ylabel(r'Probability')
    for k in range(y_T.shape[1]):
        plt.plot(T, y_T[:, k], label=f'x_{k+1}')
    plt.legend()
    plt.show()    


if __name__ == '__main__':
    experiment(x_dim=7, min_t=0, max_t=5)

Monotonic growth

이전 포스트

Prove that m, n is coprime iff Z_mn and direct sum of Z_m, Z_n is isomorphic.

다음 포스트