트리 자료구조에 관하여

트리의 정의

트리란 여러 노드가 연결된 비선형 계층구조이다.

트리의 구조

트리는 기본적으로 노드, 간선으로 이루어져 있다.

노드란 트리에서 데이터 하나를 의미하며 간선은 노드간의 연결을 의미한다.

노드의 종류

• 루트 노드: 가장 최상단에 위치하는 노드이다.
• 부모 노드: 어떤 노드의 바로 상위에 위치하는 노드이다.
• 자식 노드: 어떤 노드의 바로 하단에 위치하는 노드이다.
• 리프 노드: 자식이 존재하지 않는 노드이다.

트리의 종류

트리에는 대표적으로 이진 트리, 완전 이진 트리가 존재한다.

이진 트리란?

이진 트리는 2개 이하의 자식 노드를 가지는 트리를 일컫는 용어이다.

2개의 자식노드 중 왼쪽 노드는 Left Node라 부르며 오른쪽 노드는 Right Node라고 부른다.

완전 이진 트리란?

모든 노드가 왼쪽에서 부터 채워지는 이진 트리를 의미한다.

힙(heap)은 완전 이진 트리의 일종이다.

완전 이진 트리는 최하위 레벨을 제외하고는 자식노드가 모두 2개이며 왼쪽부터 노드가 존재한다.

트리 순회

해당 자료구조를 이용해서 프로그램을 실행시키기 위해서는 트리의 노드들을 순회하는 방법이 필요하다.

전위 순회

전위 순회는 서브트리에서 리프노드까지 순회 후 다시 올라와 남은 서브트리의 리프노드까지 순회를 반복하는 방식이다.

1. 루트 노드를 방문한다.
2. 왼쪽 서브 트리에서 깊이 우선 순회를 진행한다.
3. 오른쪽 서브 트리에서 깊이 우선 순회를 진행한다.

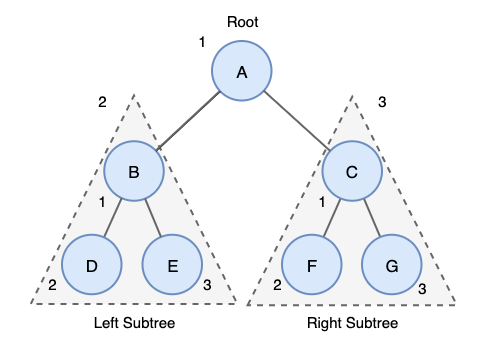
A - B - D - E - C - F - G 순서로 순회를 진행하게 된다.

중위 순회

중위 순회는 이진 탐색트리에서 오름차순 혹은 내림차순으로 값을 가져올 때 사용하는 방식이다.

1. 왼쪽 서브 트리를 중위 순회한다.
2. 루트 노드를 방문한다.
3. 오른쪽 서브 트리를 중위 순회한다.

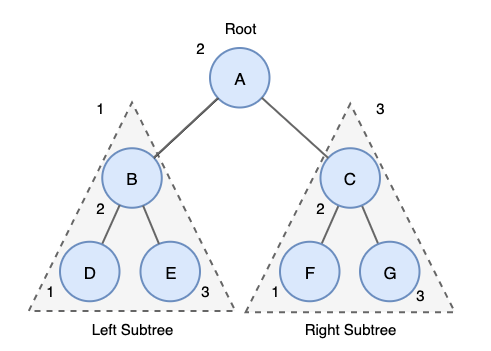
B - D - E - A - C - F - G 순서로 순회를 진행하게 된다.

후위 순회

후위 순회는 트리를 삭제하는데 주로 사용되는 방식이다.

1. 왼쪽 하단 노드부터 순회를 시작한다.
2. 루트를 거치지 않고 오른쪽 서브트리에 방문한다.
3. 오른쪽 서브트리의 왼쪽 하단 노드부터 순회를 시작한다.
4. 루트노드를 방문한다.

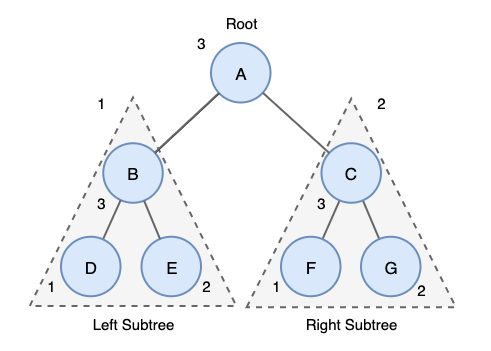
D - E - B - F - G - C - A 순서로 순회를 진행하게 된다.

트리 탐색 구현

# 전위 순회 탐색

def preorder(n): # 입력 받는 n은 루트 노드
    if n <= N:
        print(tree[n], end = ' ')
        preorder(n*2)
        preorder(n*2 + 1)
    
# 중위 순회 탐색

def midorder(n):
    if n <= N:
        midorder(n*2)
        print(tree[n], end = ' ')
        midorder(n*2 + 1)

# 후위 순회 탐색

def postorder(n):
    if n <= N:
        postorder(n*2)
        postorder(n*2 + 1)
        print(tree[n], end = ' ')


N = 9 # 노드의 수
tree = [0,'a', 'b', 'c', 'd', 'e','f','g','h','i'] # 트리

# 탐색
preorder(1)
print('\n')
midorder(1)
print('\n')
postorder(1)

힙(heap) 자료구조란?

힙이란 완전 이진 트리의 일종으로 최댓값과 최솟값을 빠르게 찾기 위해 만들어진 자료구조이다.

우선 순위 큐는 가장 우선 순위가 높은 데이터를 먼저 삭제 시키는 방식이다.

힙에는 최대 힙과 최소 힙이 존재한다.

최대 힙

부모 노드의 값이 자식 노드의 값보다 크거나 같은 완전 이진 트리

최소 힙

부모 노드의 값이 자식 노드의 값보다 작거나 같은 완전 이진 트리

힙의 삽입

1. 힙에 새로운 요소가 들어온다.
2. 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
3. 새로운 노드를 부모 노드들과 교한한다.

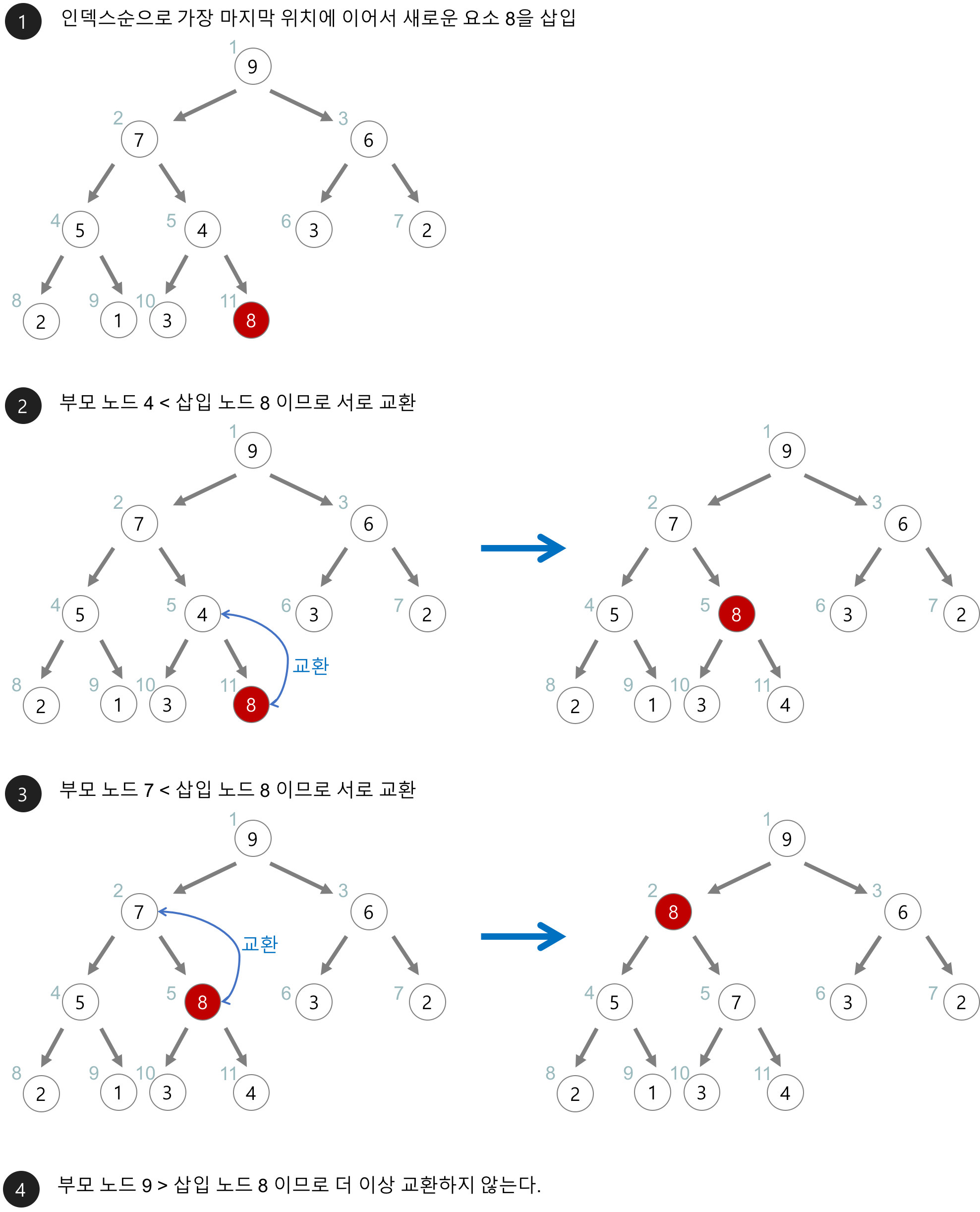
힙의 삭제

1. 최대 힙에서 최댓값은 루트 노드이므로 루트 노드를 삭제시킨다.
2. 삭제된 루트의 노드에는 힙의 마지막 노드를 가져온다.
3. 자식 노드와 교환을 진행하며 힙을 재구성한다.

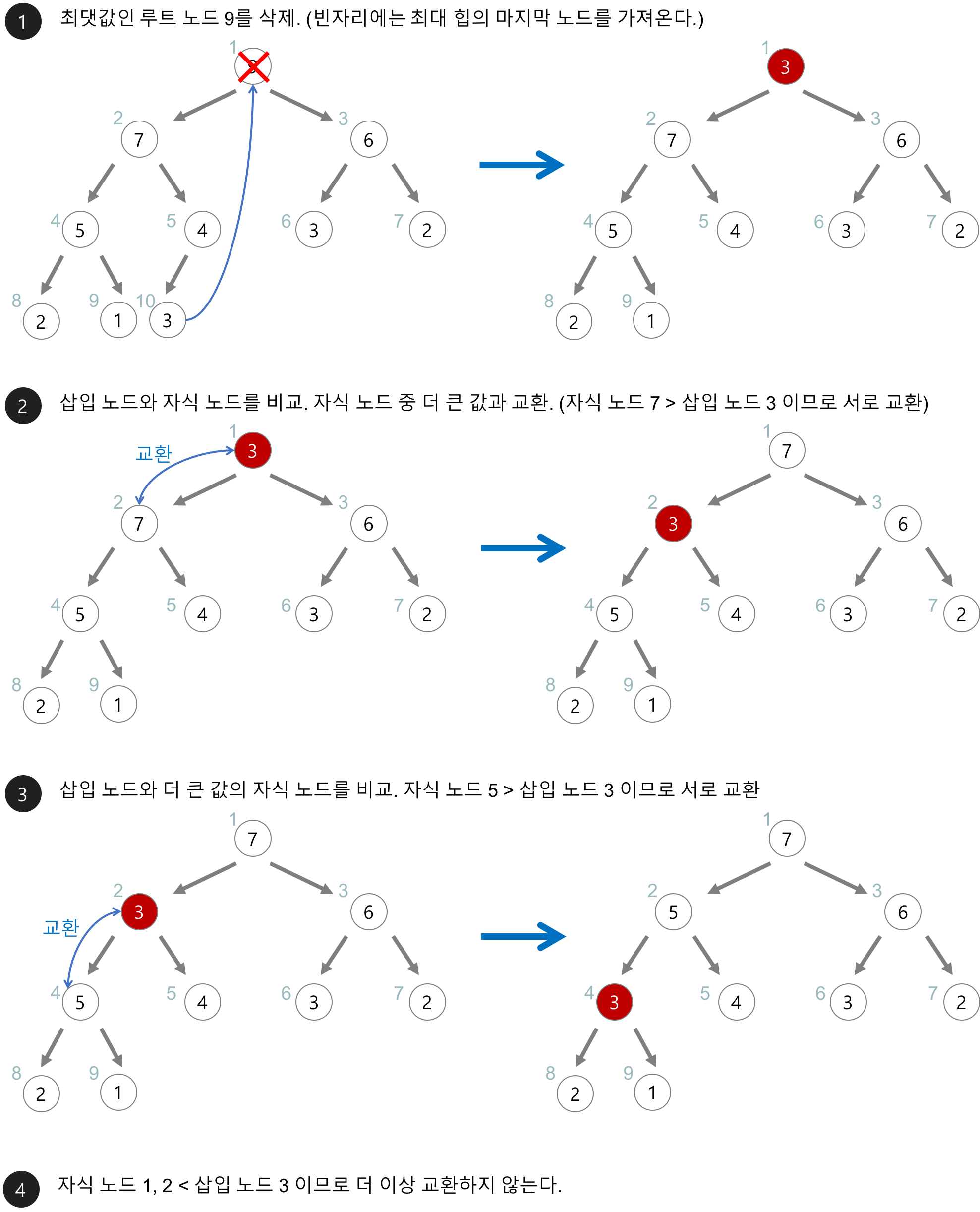
힙의 삽입 및 삭제 구현

// 최대 힙 삽입
void insert_max_heap(int x) {
    
    maxHeap[++heapSize] = x; // 힙 크기를 하나 증가하고, 마지막 노드에 x를 넣음
    
    for( int i = heapSize; i > 1; i /= 2) {
        
        // 마지막 노드가 자신의 부모 노드보다 크면 swap
        if(maxHeap[i/2] < maxHeap[i]) {
            swap(i/2, i);
        } else {
            break;
        }
        
    }
}

// 최대 힙 삭제
int delete_max_heap() {
    
    if(heapSize == 0) // 배열이 비어있으면 리턴
        return 0;
    
    int item = maxHeap[1]; 		// 루트 노드의 값을 저장
    maxHeap[1] = maxHeap[heapSize]; 	// 마지막 노드 값을 루트로 이동
    maxHeap[heapSize--] = 0; 		// 힙 크기를 하나 줄이고 마지막 노드 0 초기화
    
    for(int i = 1; i*2 <= heapSize;) {
        
        // 마지막 노드가 왼쪽 노드와 오른쪽 노드보다 크면 끝
        if(maxHeap[i] > maxHeap[i*2] && maxHeap[i] > maxHeap[i*2+1]) {
            break;
        }
        // 왼쪽 노드가 더 큰 경우, swap
        else if (maxHeap[i*2] > maxHeap[i*2+1]) {
            swap(i, i*2);
            i = i*2;
        }
        // 오른쪽 노드가 더 큰 경우, swap
        else {
            swap(i, i*2+1);
            i = i*2+1;
        }
    }
    
    return item;
    
}