선형대수 (1)

Chatper 1 벡터

1) 벡터의 정의와 표기법

• 벡터: 물리학 및 공학에서 위치, 속도, 힘 등과 같이 크기와 방향성을 나타냄

• 공학에서는 벡터 공간이 유클리드 공간인 경우를 다룸

• 유클리드 벡터, 기하 벡터, 공간 벡터라고 부름

• 벡터와 대비하여 크기만을 갖는 대상을 스칼라라고 함
  

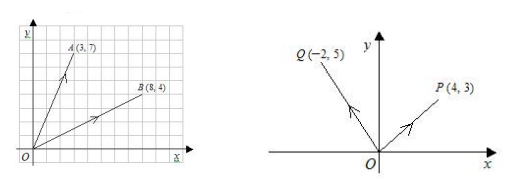
• 벡터의 표기

• 한 벡터를 부호 a로 사용하여 나타낼 때, $\vec{a}$

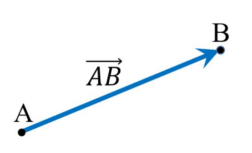
• 점 A에서 점 B를 향하며, 크기가 두 점 사이를 잇는 선분의 길이인 벡터: $\overrightarrow{AB}$

• A를 화살표의 원점, 기점, 꼬리라고 하며, B는 화살표의 끝, 종점, 머리라고 표현
  

2) 벡터의 기본적인 성질

벡터의 기본적인 성질

• 동등성 : 벡터가 크기와 방향만을 가지므로 원점의 특정한 위치는 아무런 의미를 갖지 않음. 즉, 원점이 일치하지 않더라도 두 화살표의 방향이 일치하고 그 크기가 같으면, 동일한 벡터임
• 영 벡터 : 영벡터는 크기가 영인 벡터를 의미함
• 음 벡터 : 벡터 a 자신에 더했을 때 결과가 영벡터가 되는 벡터를 a의 음벡터라고 정의함. –a로 표시하고 음 벡터 –a는 a와 크기는 같으나 방향이 정반대인 벡터를 의미함

벡터의 좌표와 성분

• 벡터를 표현하는 방법으로 공간에 좌표계를 설정하여 좌표 값을 사용할 수 있음
• 기하학적으로 벡터를 다루는 방법보다 편리하며, 보다 체계적으로 정확한 계산을 할 수 있음
• 가장 흔한 예로는 직각좌표계를 사용함. 한 벡터의 기점을 좌표계의 원점으로 하고 벡터의 종점의 좌표로 해당 벡터를 표시함
  

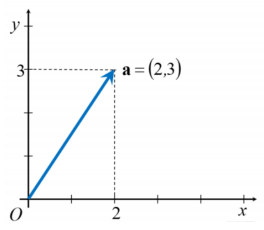
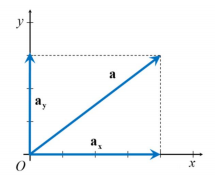
벡터의 성분,분해,합성

• 벡터를 성분은 각각의 좌표축에 벡터를 투영시켜(Projection) 얻음.
• 이 또한 벡터이므로 성분벡터(Component vector, $𝑎_𝑥$, $𝑎_𝑦$)라고 부름
• 따라서, $𝑎_𝑥$, $𝑎_𝑦$는 “벡터 a의 축 성분벡터”라고 부름
• 이것은 2차원 이상의 공간에서는 차원의 수 만큼 성분이 존재하며, 차원을 확장하여 적용 가능
• $a = 𝑎_𝑥 + 𝑎_𝑦$ 로 표현이 가능함
• 한 벡터를 자신의 성분벡터들의 합으로 나타내는 것이 벡터의 분해라고 함
  

단위 벡터

• 단위 벡터는 크기가 1이며, 특정한 방향을 갖는 벡터

• 3차원의 직각좌표계 (X, Y, Z)가 주어질 때, 각 좌표축에 나란한 방향을 갖는 단위벡터를 각각 $\hat{i}$, $\hat{j}$, $\hat{k}$ 라고 나타냄
  

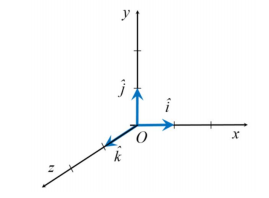
• 축의 방향은 '오른나사 규칙', '오른손 규칙'의 관례를 따라 정함

• 모든 좌표축에 대한 단위 벡터들의 집합을 기저벡터 집합이라고 부름

• 특정 기저벡터 집합을 선택하는 것은 특정한 직각좌표계를 선택하는 것과 동등

• 스칼라 배의 정의를 이용하여 벡터 a의 성분 벡터들은 아래와 같이 표현 가능
  

3) 벡터의 연산

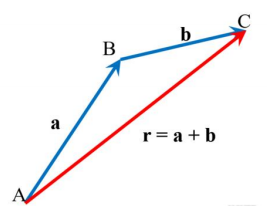
벡터의 덧셈

• 기하학적인 방법: 삼각형법
• 공간 상의 위치는 벡터량, 위치의 변화인 변위(displacement)도 벡터량
  

덧셈의 교환법칙

• 두 벡터의 순서가 바뀌어도 결과는 동일
  

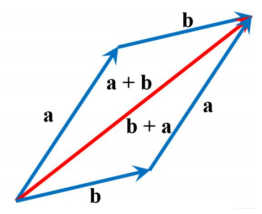
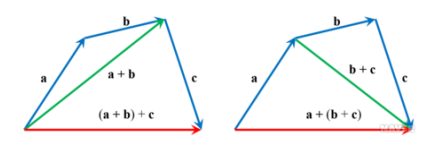
덧셈의 결합법칙

• 더하는 벡터들이 2개 이상인 경우에도, 더하는 순서에 상관없이 결과가 동일
  

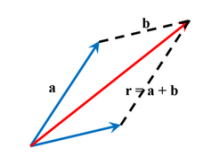
평행사변형법

• B를 평행 이동하여, a와 b의 꼬리를 일치시킨 후, 두 벡터를 인접한 두 변으로 하는 평행사변형을 그렸을 때, 두 벡터의 꼬리에서 시작하는 평행사변형의 대각선이 a와 b의 합벡터
  

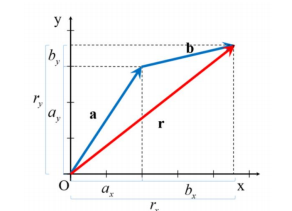
성분을 이용한 대수적인 방법

• 두 벡터가 동일하다면 대응하는 벡터의 성분이 반드시 같아야 함
  

벡터의 뺄셈

• 자기 자신과 크기는 같고 방향이 정반대인 음벡터의 정의를 이용

벡터의 곱셈

• 내적(inner product):스칼라 값의 결과가 나옴
• 외적(outer product): 벡터 값의 결과가 나옴

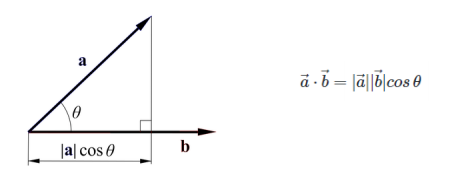
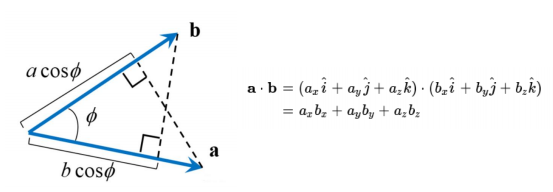
벡터의 내적

• 내적은 벡터를 수처럼 곱하는 개념
• 방향이 일치하는 만큼만 곱함
• 두 벡터가 이루는 각이 90도 일 때는 일치하는 정도가 없어서 0
• 내적은 한 벡터를 다른 벡터로 투영, 정사영 시켜서 그 벡터의 크기를 곱함
  
  

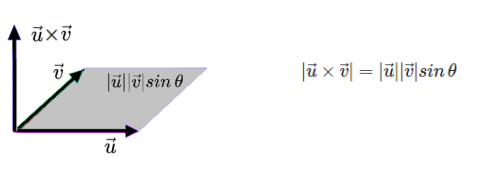
벡터의 외적

• 외적의 결과 값은 벡터, 방향은 두 벡터 a,b가 이루는 평면에 수직
• 직각 좌표계에서 단위 벡터들은 서로 수직하므로, 서로 다른 단위벡터들의 벡터곱은 크기가 1이고 나머지 단위벡터에 나란한 방향
• 자기 자신과의 벡터곱은 사이각이 0이므로 모두 0
  
  
  

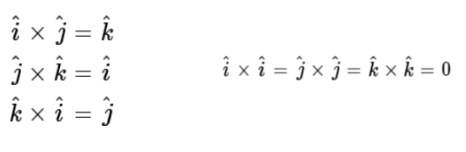
Chapter 2 행렬

1) 행렬의 정의

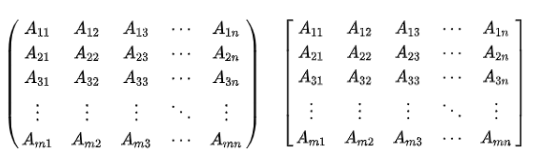
• 행렬을 이용하면 복잡한 자료를 이용한 어려운 계산도 쉽게 풀 수 있고 해석도 직관적으로 가능함
  
  

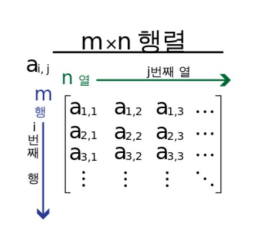
• 행렬 A의 크기는 행과 열의 수의 순서쌍(m,n) 또는 m * n을 뜻함

• 만약 행과 열의 수가 같다면, A를 정사각행렬 또는 정방행렬이라고 함

• m=1이면 행 벡터, n=1이면 열 벡터
  

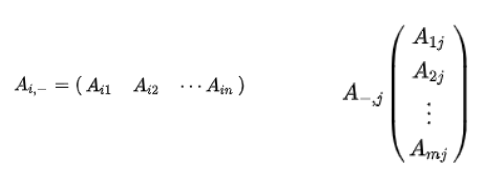
2) 행렬의 계산

• 위치가 같은 원소끼리 더하거나 빼줌
  

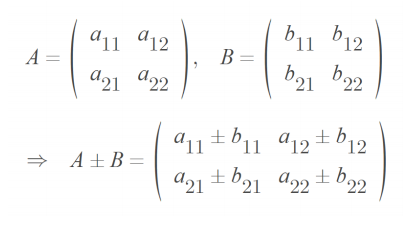
• 행렬의 상수배는 행렬의 각 성분에 임의의 실수를 곱합
  

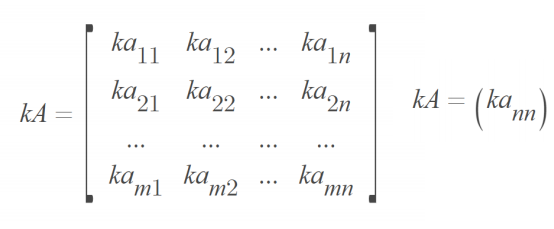
• 행렬의 곱하기는 행렬의 열의 수와 곱해지는 행렬의 행의 수가 같을 때만 가능

• 결과로 나오는 행렬의 크기는 앞 행렬의 행 수와 뒤 행렬의 열 수
  
  
  

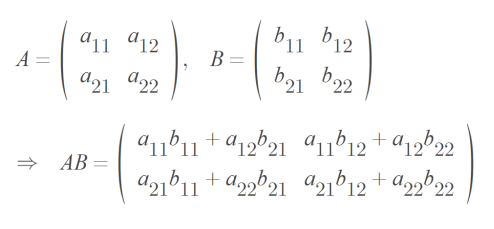
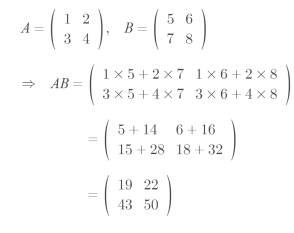
• 행렬의 곱은 AB와 BA가 같지 않음(교환 불가)

• 행렬 [m x n], 행렬 [n x k]를 곱했을 때 [m x k]
  

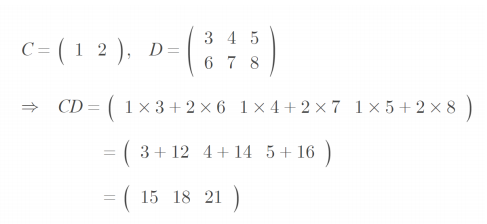
• 전치행렬: 행렬을 뒤집어 놓은 형태
  

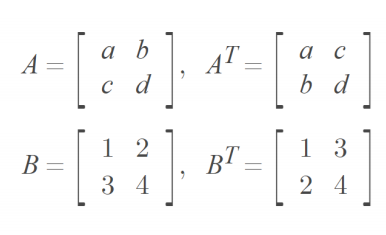
• 역행렬
  
  

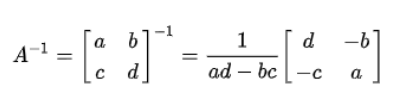
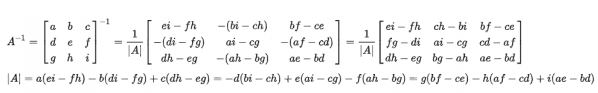
3) 기타 특수 행렬

• 단위행렬
  

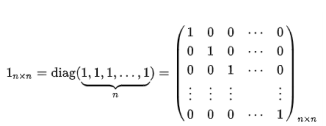
• 대각행렬
  

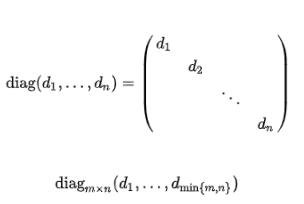
• 삼각행렬
  

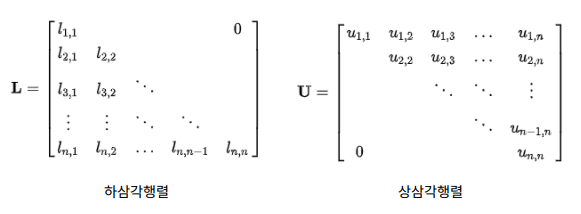
• 대칭행렬
  

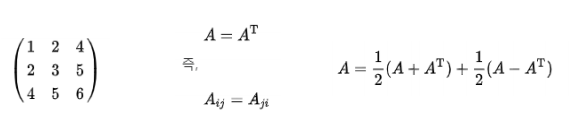
• 반대칭행렬
  

이 글은 제로베이스 강의 자료 일부를 발췌하여 작성되었습니다