선형대수 (2)

Chapter 3 선형대수학

1) 선형 방정식 소개

• 선형 방정식:linear equation
  

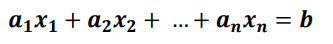
• 비선형 방정식: nonlinear equation
  

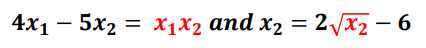
• 선형 방정식 계(A system of linear equation): 같은 변수들을 포함한 선형 방정식이 1개 또는 그 이상의 집합을 의미
  

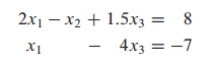
• 해의 집합(Solution set): 선형 시스템에서 모든 가능한 해의 집합

• 상등(Equivalent): 두 선형 시스템에 같은 해의 집합을 가지고 있다면 두 선형 시스템은 상당함
  -> 같은 해의 집합을 갖는 선형방정식 간의 관계를 행 상등이라고 함
  

• 해가 없다(Inconsistent)
  -> 두 직선이 평행하면 교차점이 없음, 이 경우가 no solution이며, 두 방정식은 inconsistent라고 함
  

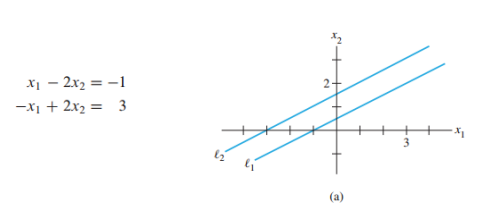
• 해가 있다(consistent)
  -> 해가 하나인 경우
  
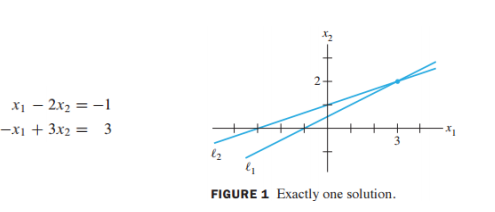
  -> 해가 무수히 많은 경우
  

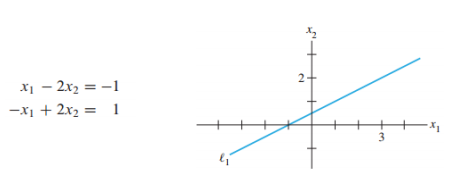
• 선형 방정식 계는 no solution, exactly one solution, infinitely many solution

• Inconsistent: no solution을 의미

• Consistent: exactly one solution, infinitely many solution을 의미

• 2개의 해가 존재하는 경우는 비선형
  

• 행렬 표기법(matrix notation): 선형시스템을 행렬로 표현한 것
  

• 계수행렬(coefficient matrix): b를 제외하고 a만을 행렬로 나타낸 것

• 첨가행렬(augmented matrix): b까지 포함한 행렬
  

2) 소거법(Elimination)

선형방정식의 n=2 일 때 행관점과 열관점

• 행 관점의 선형 방정식 접근
  -> 두 개의 식이 X, Y 좌표에 표시할 수 있고 두식이 교차하는 점에서 해가 존재함
  

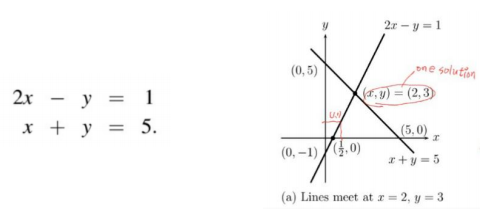
• 열 관점으로 선형 방정식 접근
  -> (2,1) vector에 2(x)를 곱하고 (-1, 1) vector에 3(y)을 곱함
  -> 위와 같이 곱하게 되면 (4, 2) + (-3, 3) = (1, 5)가 됨
  

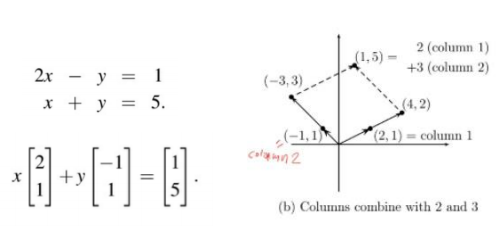
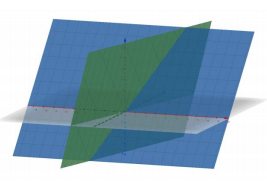
선형방정식의 n=3일 때 행관점과 열관점

• 행 관점으로 선형 방정식 접근
  -> Row picture: 평면들의 교차점(intersection of plans)
  

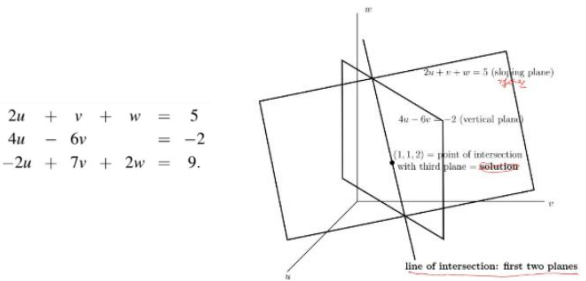
• 열 관점으로 선형 방정식 접근
  -> Column picture: 열들의 결합(Combination of columns)
  
  
  

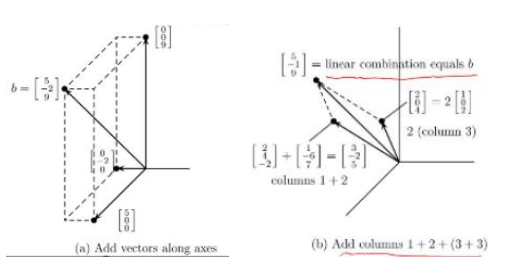
소거법(Elimination)

• 행 연산(row operation)을 통해 소거법(elimination)을 진행하고 선형 방정식(linear equation)의 해(solution)을 구할 수 있음

• 가우스 소거법에서 행할 수 있는 기본 행 연산(elementary row operations)
  -> 0이 아닌 상수를 행에 곱할 수 있다. (scaling)
  -> 두 행을 교환할 수 있다. (interchange)
  -> 한 행을 상수배 하여 다른 행에 더할 수 있다. (replacement)

• 상/하삼각행렬을 만들어 해를 찾음
  

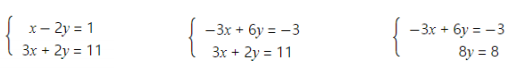
• 가우스 소거법
  -> 1) 선형 방정식 계를 행렬로 표현
  
  -> 2) 마지막 행의 $𝑥_1$의 계수를 0으로 만듦
  
  -> 3) 마지막 행의 $x_2$의 계수를 0으로 만듦
  
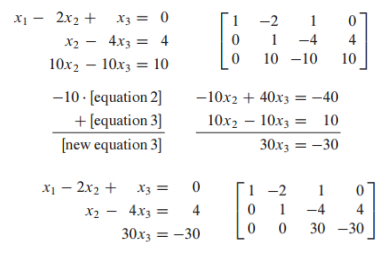
  -> 4) 마지막 행의 $x_3$의 계수를 1로 만듦: 상삼각행렬 완성
  
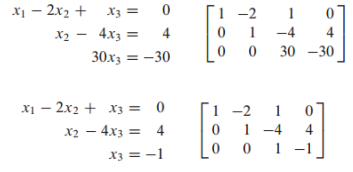
  -> 5) $x_3$을 알았으므로 대입을 통해 $x_1$, $x_2$의 값을 구함
  

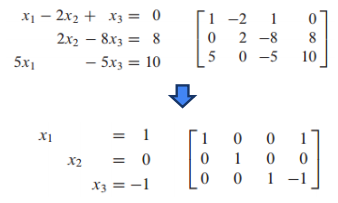
• 행 연산 과정이 하나의 행렬을 다른 행렬로 변환된다면 두 행렬은 행 상동하다고 할 수 있음
• 두 선형 시스템이 행 상동하다면 두 시스템은 동일한 해의 집합을 가지고 있음

3) 선형 방정식의 특이한 경우

• The Singular Case
  -> 1) 해가 없는 경우: 평행
  
  -> 2) 세 개의 평면이 평행하지 않는 경우
  
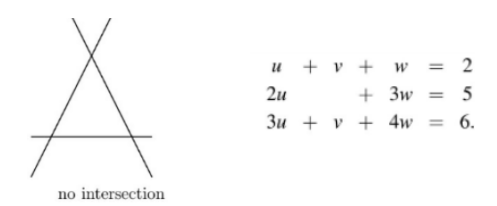
  -> 3) 세 개의 평면이 평행한 경우
  
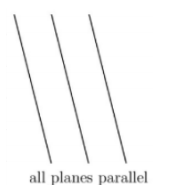
  -> 4) 해가 무수히 많은 경우(infinity of solution)
  

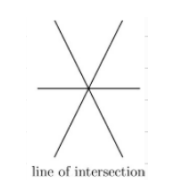
• 시스템이 특이할 때 column picture
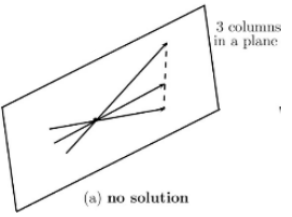
  -> 1) 해가 없는 경우: 3개의 column이 동일한 평면에 놓이고 b는 다른 평면에 위치할 때 해가 없음
  
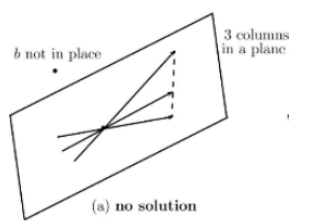
  -> 2) 해가 무수히 많은 경우: b가 3개의 열들과 동일한 평면에 놓여져 있을 때 b를 만들기 위해 3개의 열들은 무수히 많은 방법으로 결합 될 수 있음
  

4) 역행렬

• 역행렬이 존재하는 행렬: Invertible Matrix
• 2 X 2 행렬의 결정자(det = ad - bc) - Determinant
• 기본행렬: Elementary Matrix
• $A^{-1}$를 찾는 알고리즘

숫자의 승수 역수: Multiplicative inverse of a number

• 5의 역수는 1/5
  

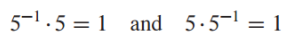
역행렬이 존재하는 행렬

• Row와 Column의 크기가 동일해야 함
• AC = I 인 C 행렬이 있어야 하며 C는 유일(unique) 해야 함
• Matrix가 not invertible이면 singular matrix(해가 존재하지 않는 행렬)임
• invertible이면 nonsingular matrix(해가 존재)함
  

이론

• A가 2x2 행렬일 때 ad-bc !=0 이면 A는 invertible 함

• ad-bc = 0 이면 not invertible 임

• 여기서 ad-bc는 pivot position이 2개 있을 조건을 의미하며 determinant(결정자)라고 불림

• 어떤 matrix가 invertible을 판단할 때 determinant가 0인지 아닌지를 확인해야 함
  
  

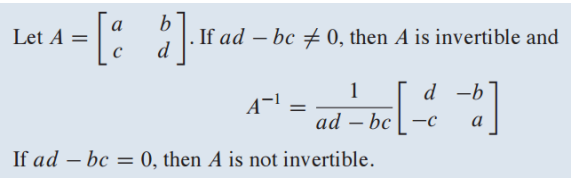
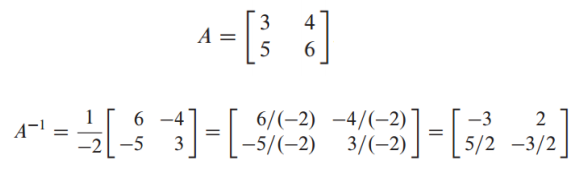
• A가 invertible [n x n] matrix이면 $𝑅^𝑛$ 공간에 있는 b에 대한 방정식 $𝐴𝑥 = 𝑏$는 유일한 해를 갖음

• $𝑥 = 𝐴^{−1}𝑏$

• A의 inverse를 이용하면 쉽게 solution을 구할 수 있음
  

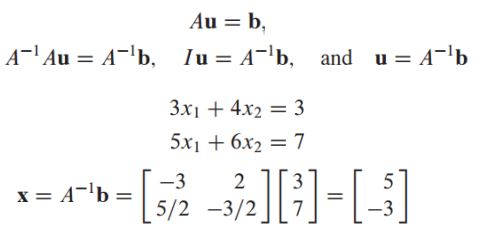
• A가 invertible matrix 이면 $A^{-1}$도 invertible

• $(AB)^{-1}$ = $B^{-1}A^{-1}$
  

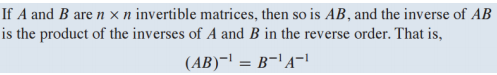
• A가 invertible이면 $A^T$도 invertible
  

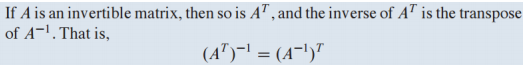
기본행렬: Elementary Matrices

• 기본 행렬은 항등 행렬에 단일

• 기본 행 연산을 적용해서 얻어짐
  

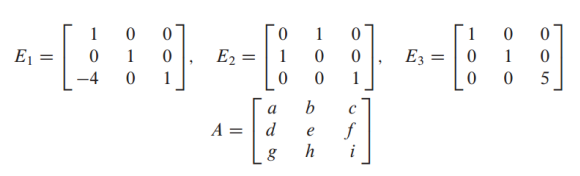
• $E_1$은 replacement를 적용한 행렬

• $E_1A$는 A에 replacement를 적용한 것과 동일한 값이 나옴

• $E_2$는 interchange를 적용한 행렬

• $E_3$는 Scaling을 적용한 행렬, 이를 A와 곱하면 A에도 행 연산을 적용한 결과가 나
  

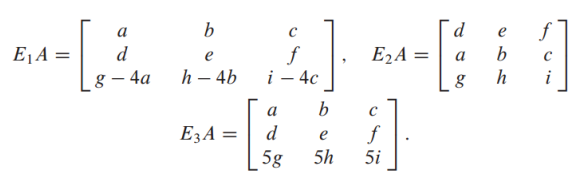
• [m x n] matrix에 elementary row operation을 수행했다는 것은 어떤 m x m elementary matrix가 존재한다는 의미

• A에 적용한 row operation을 m x m identity matrix에 적용하면 E가 생성 됨

• Elementary matrix E가 invertible이면 E의 inverse는 E를 I로 변환하는 elementary matrix 임

$A^{-1}$를 찾는 알고리즘

• A가 [m x n] 이고 invertible이면 항등 행렬(identity matrix)를 이용해서 $A^{-1}$ 를 찾을 수 있음
  

5) 역행렬 특징

역행렬 이론(The invertible Matrix Theorem)

• A가 invertible이면 아래 조건을 다 만족하고 not invertible이면 아래 조건을 만족하지 않음
  

역선형 변환(Invertible Linear Transformation)

• Linear Transformation이 invertible이라고 불릴 조건은 아래와 같음
• X의 image에 S 함수를 위하면 원래 X로 돌아옴, S함수가 존재하는 경우에는 T는 Invertible 함
  
  

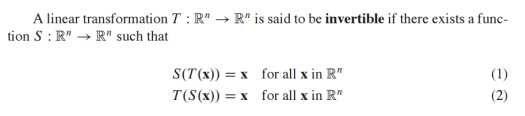
이론

• 선형 변환(linear transformation)은 항상 표준 행렬(standard matrix)가 존재함
• T가 invertible이면 A(standard matrix)도 invertible함
• 또, 선형 변환 S 함수는 $S(x) = 𝐴^{−1}𝑥$ 로 주어짐

이 글은 제로베이스 강의 자료 일부를 발췌하여 작성되었습니다