Chapter 3 선형대수학
10) 특성 방정식
특성방정식(Characterisitic equation)
-
특성방정식은 det(A- 𝜆I) = 0을 의미함
-
𝜆가 특성방정식을 만족하면 𝜆는 행렬 A의 eigenvalue임
-
예시
-> 𝜆(eigenvalue)는 5, 3, 1이 됨
-> 여기서 eigenvalue 5는 곱(multiplicity) 2를 갖음
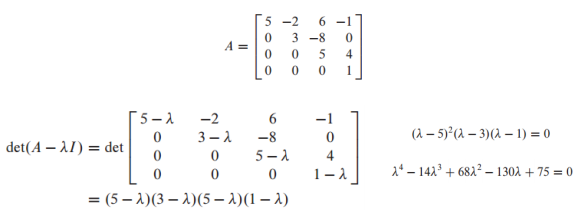
유사도(Similarity)
- n차 방정식에서 eigenvalue를 찾는 것은 쉽지 않아 similarity를 주로 사용함
- 이 성립할 때 A는 B에 similar라고 표현함
- similarity transformation은 로 변환하는 transformation을 의미 함
이론
- eigenvalue를 찾을 때 similar한 matrix를 찾아서 eigenvalue를 찾음
- 일반적인 경우에 eigenvalue를 구하는 것은 다루기가 어려우므로 특수한 성질을 갖는 matrix의 eigenvalue는 상대적으로 쉽게 구할 수 있음
- A와 B가 similar이고 동일한 특성 polynomial을 갖고 있으면 두 행렬은 동일한 eigenvalue를 갖음 - eigenvalue는 동일하지만 eigen vector space는 보통 다름
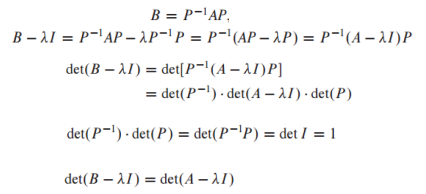
11) 대각화
대각화(Diagonalization)
- 정사각행렬(square matrix) A가 대각 행렬(diagonal matrix)와 유사(similar)하면 A를 대각화 가능(diagonalizable)하다고 함
- 즉, 일 때 A가 diagonalizable이라고 함
- diagonal matrix의 square은 diagonal term의 square임
- 만약 A가 D와 similar하면 를 쉽게 구할 수 있음
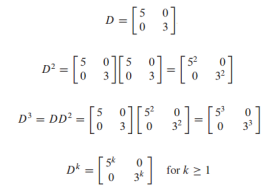
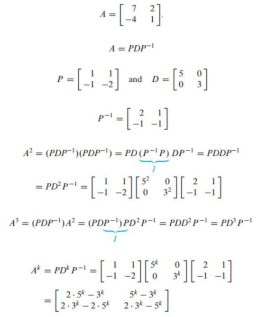
이론
- n x n 행렬 A가 diagonalizable이면 A는 n개의 linearly independent eigenvector를 갖고 있음
- 즉, D가 diagonal matrix이고 이면, P의 column은 A의 n개의 linearly independent eigenvector로 이루어져 있음
- 이 경우에 D의 diagonal entries는 P를 구성하는 eigenvector 각각에 대한 A의 eigenvalues 임

- p가 로 이루어진 행렬이고 D가 eigenvalues를 diagonal entries로 갖고 있는 diagonal matrix이면 아래와 같음
- P가 invertible이므로 이 성립됨
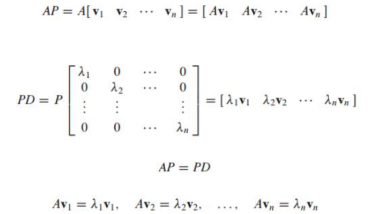
행렬 대각화하기(Diagonalizing Matrices)
(1) 행렬의 eigenvalues를 찾기: 특성 방정식을 이용해서 찾을 수 있음
(2) 행렬의 eigenvector를 찾기
-> 𝜆에 대한 basis를 의미함
-> eigenvector를 찾기 위해서는 (A-𝜆I)x = 0의 general solution을 찾고 eigenvector를 찾고 eigenspace를 찾아서 basis를 찾아야 함
-> eigenvector를 찾았으면 n개 인지 확인(n개 보다 작으면 대각화 불가능)
(3) eigenvector로 P를 구성
(4) D는 diagonal entries가 eigenvalues인 diagonal matrix임
-> 앞에서 구한 eigenvalues로 D 행렬을 구성
-> 주의할 점으로는 P의 eigenvector에 해당되는 eigenvalue를 diagonal entry로 두어야 함
- 예시

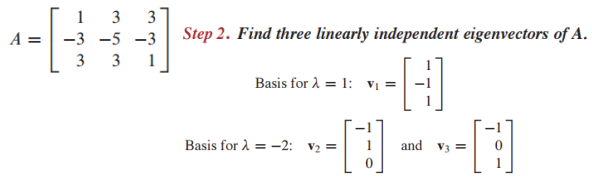


12) 대칭 행렬의 대각화
대칭 행렬
- 대칭 행렬은 행렬 A가 정사각행렬(square matrix)이고, 를 만족하는 행렬
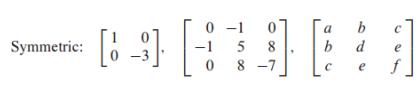
이론
-
대칭 행렬의 특성은 A행렬이 대칭 행렬이면, 고유 벡터는 직교함
-
v1, v2가 서로 다른 고유치 𝜆1, 𝜆2에 해당하는 고유 벡터일 때, v1*v2 = 0의 증명은 아래와 같음
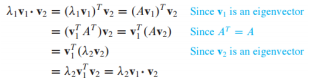
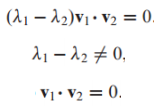
-
두 고유 값은 서로 다른 값이므로 차는 0이 아님
-
따라서 고유 벡터 v1, v2의 내적이 0일 수 밖에 없음
-
이러한 대칭 행렬의 성질 때문에 대칭 행렬의 대각화를 “직교 대각화 가능” 이라고 함
직교 대각화 기능(orthogonally diagonalizable)
- 만약 이 성립하면 행렬 A는 orthogonally diagonalizable 이라고 함
- 여기서, P는 정규 직교(orthogonal) 벡터로 이루어진 직교 행렬이고, 를 성립함
- 대칭 행렬은 를 만족함
- 실제로 A가 orthogonally diagonalizable할 때, 를 만족하는지 아래와 같이 확인해 봄 - orthogonally diagonalizable이면 가 성립
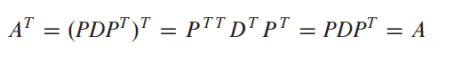
스펙트럼 정리(Spectral Theorem)
-
행렬 A의 고유 값 집합을 A의 스펙트럼이라고 부름. A가 대칭 행렬일 때, 다음과 같은 성질을 따름
-> A가 n개의 고유치를 갖고 있으면 multiplicity를 계산함
-> 각 고유치에 해당하는 고유공간의 차원은 고유치의 multiplicity와 동일함
-> 고유공간은 서로 직교함. 서로 다른 고유치에 해당하는 고유벡터도 직교함
-> A는 orthogonally diagonalizable 함 -
스펙트럼 분해는 행렬 A를 eigenvalue(spectrum)으로 표현되는 조각들로 분해하는 것
-
행렬 A가 orthogonally diagonalizable하다고 가정하고, 다음과 같이 표현할 수 있음
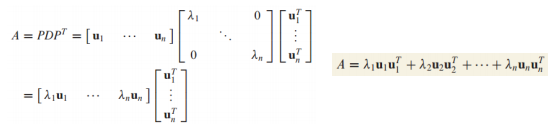
-
A를 위와 같이 표현한 것을 A의 스펙트럼 분해라고 함
-
그리고 각 요소 는 Rank가 1인 n x n 행렬임
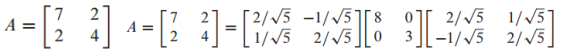
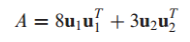
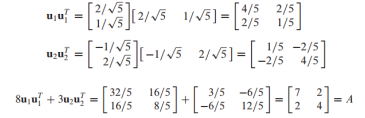
13) 특이값 분해(SVD)
- 대칭행렬의 대각화에서 배웠던 대각화 이론은 많은 분야에 적용될 수 있음
- 하지만, 모든 행렬이 로 분해 되지 않음
- D가 대각행렬이기 때문에 A는 m x m 행렬이어야지 대각화를 할 수 있음
- 특이값 분해 는 행렬의 크기(m x n)와 상관 없이 대각화가 가능함
M x n 행렬의 특이값
- m x n 크기의 행렬 A의 특이값(singular values)는 의 고유값(eigenvalue)에 루트를 씌운 값임 - 그리고 σ로 표기함
- 는 n x n 크기의 대각행렬(symmetric matrix) 임
- 그리고 대각 행렬은 대각 요소가 동일하므로 전치를 해도 원래 행렬이 되는 특징과 직교 대각화가 가능함
- 행렬을 직교 대각화 한 뒤에, 고유값을 구하고 그 고유값에 루트를 취하면 A행렬의 특이값을 구할 수 있음
- 그리고 A의 특이값(singular value)는 벡터의 길이이며 의 고유 값에 루트를 취함

특이값 분해
-
이 행렬의 크기가 m x n이고, r x r 크기의 대각 요소가 특이 값인 대각 행렬 D를 포함함
-
r은 m이나 n을 초과하지 않음
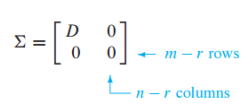
-
특이 값 분해는 행렬 A를 다음과 같이 분해하는 것
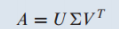
-
U는 {}을 정규화한 {} 벡터가 열들로 이루어진 행렬
-
A의 left singular vector로 부름
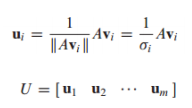
-
V는 의 정규직교 고유벡터가 열들로 이루어진 행렬임
-
A의 right singular vector로 부름
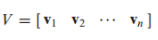
13) Reduced SVD, 유사역행렬
Reduced SVD
-
A 행렬을 SVD하면 아래와 같음
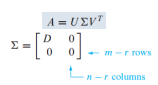
-
위 행렬은 대각 행렬인 D를 포함하는데, D 행렬은 대각 요소가 특이값(singular value)로 이루어진 rxr 크기의 행렬임. R행, r열까지는 특이 값이 이루어져 있고, r+1 행과 r+1 열 부터는 값이 0임
-
U와 V가 r+1행, r+1열 부터는 0과 곱해져 0이 되는 것임
-
어차피 r을 초과하는 인덱스는 0과 곱해져 0dl 되므로 U와 V행렬을 r까지만 표기한 것이 Reduced SVD임
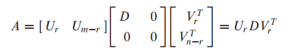
유사역행렬(Pseudo inverse)
-
유사역행렬은 를 정의해서 최소제곱법(least-square solution)을 구하는데 이용함
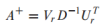
-
Ax=b를 풀고자 할때, x를 다음과 같이 정의함

-
의 양변에 A를 곱해 방정식을 풀면 다음과 같이 A는 reduced SVD로 분해한 값을 대입하게 됨
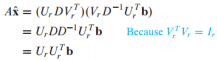
-
은 column A를 span하는 정규 직교 기저임, b를 Column A에 projection한 것과 동일
-
는 b를 column A에 projection한 것이 되고, 은 Ax=b의 최소제곱법이 됨
이 글은 제로베이스 강의 자료 일부를 발췌하여 작성되었습니다
