선형대수 (3)

Chapter 3 선형대수학

6) LU 분해

**분해(Factorizaiton, Decomposition)

• 하나의 행렬을 두개 혹은 3개 이상의 행렬 곱으로 표현한 식
• A행렬을 B와 C의 곱으로 표현한 형태를 분해라고 함(A = BC)

LU 분해(LU Decomposition)
1) A의 역행렬을 이용: 모든 경우를 구해야 하므로 비효율적
2) LU 분해: 행 줄임으로 A를 LU분해하여 방정식을 푸는 것이 효과적

LU 분해의 유용성

• A = LU로 분해하였을 때 Ax = b 방정식을 다음과 같이 표현할 수 있음
• A = LU -> Ax = b -> LUx = b -> Ux = y(치환) -> Ly = b -> Ux = y -> x의 해를 찾음
• L과 U는 pivot을 사용해서 나머지 entry를 0으로 만들 수 있는 쉬운 형태로 이루어져 있기 때문에 빠르게 문제를 풀 수 있음
  

예시

• LUx = b
  

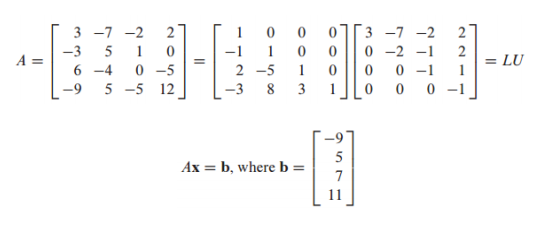
• Ux = y
  

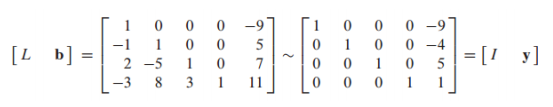
• Ly = b -> Ux = y -> x의 해를 찾음
  

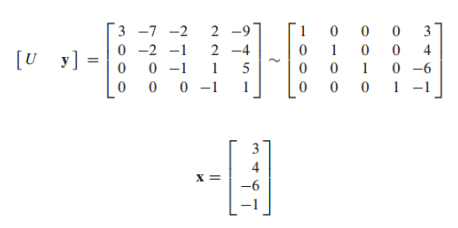
LU 구하는 방법

• A가 row replacement만을 사용하여 사다리 꼴(echelon form) 형태로 변환될 수 있다고 가정
• U(echelon form)로 변환하기 위한 행 줄임(row operation) 기본 행렬 E1, … , Ep 가 존재함
• 이 기본 행렬의 역행렬(inverse)이 L이 됨 (A가 [m x n]일 때, L은 [m x m], U는 [m x n]이 되어야 함)
  

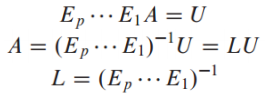
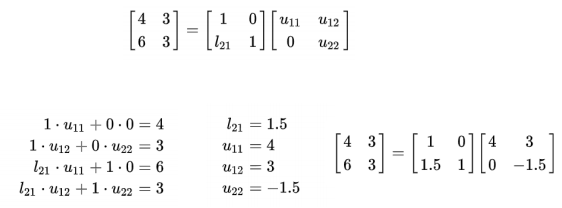
• A가 4개의 행을 갖고 있으므로 L은 4x4가 되어야 함
  
• L은 A의 각각 pivot column에서 pivot 아래의 entry를 pivot으로 나눠주면 구할 수 있음
  

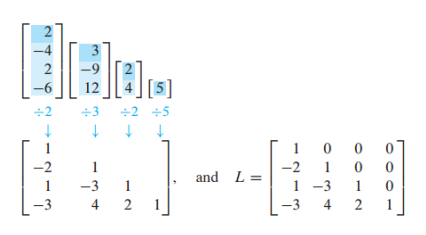
수와 관련된 메모 – Numerical Notes

• $𝐴^{−1}$로 해를 구했을 때 보다 LU분해의 연산량이 1/3배 적음
• A가 sparse(대부분 0으로 채워져 있는 경우)하면 L과 U도 sparse 함 - 하지만 𝐴−1는 dense(값이 많은 경우)함.
• 이 의미는 L과 U를 저장하는 memory와 $𝐴^{−1}$ 값을 저장하는 memory의 차이가 큰 것
• 공학적인 문제를 풀 때 LU분해는 속도와 메모리적 측면에서 큰 이점이 있음

7) 행렬식 개요

계수(Rank, Pivot, Null space)

• 행렬 A의 Rank는 A의 column space의 dimension을 의미함
• column space의 basis vector가 몇 개 존재하는지 알면 그것이 dimension이 되는 것
• A를 row reduction을 통해 echelon form(사다리꼴)로 변환하고 pivot column을 찾음
• pivot column이 3개 존재하므로 rank A는 3임
• 추가적으로 null space의 dimension은 free variable $𝑥_3$ , $𝑥_5$ 2개 이므로 dim Null A = 2 임
• Null space의 dimension은 free variable의 개수와 같음
  

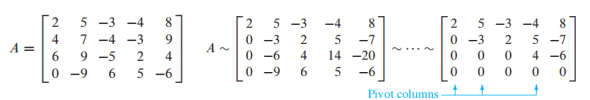
행렬식(determinant)

• 2x2 행렬에서의 determinant가 nonzero이면 invertible
  

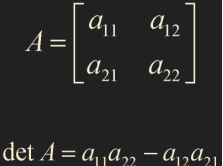
• 2 x 2 행렬에서의 determinant를 구하는 건 비교적 쉬운 일

• 3 x 3 이상 행렬 부터는 determinant를 구하는 것이 복잡해 짐

• determinant가 0이 아닌 것의 의미는 모든 row에 pivot이 존재한다는 의미

• 따라서, row reduction을 진행하고 모든 pivot이 nonzero임을 확인하면 됨
  

• 2 x 2 matrix에서 determinant는 아래와 같으므로 △을 다음과 같이 표기 할 수 있음
  

• $𝐴_{13}$ 은 1th row와 3th column을 제외한 요소들을 의미함

• A가 아래와 같이 주어졌을 때, $𝐴_{32}$ 은 다음과 아래와 같이 표기할 수 있음(3th row, 2th column 제거)
  

• A 행렬이 주어졌을 때 determinant를 계산하는 예시
  

여인수(Cofactor)

• cofactor를 이용해서 determinant를 여러가지 형태로 표현할 수 있음

• 이를 여인수 전개(cofactor expansion)이라고 함
  

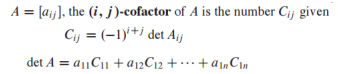
• cofactor의 부호는 $(−1)^{𝑖+𝑗}$ 는 다음과 같은 규칙을 갖음
  

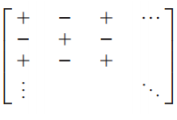
• cofactor expansion을 이용하면 row와 column으로 determinant를 표현할 수 있음

• Spare 한 row나 column을 선택해서 계산하면 빠르게 계산할 수 있음
  

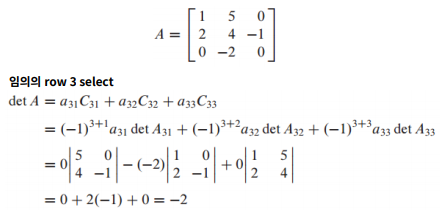
det EA = (det E)(det A)

• E는 기본 행렬(elementary matrix)를 의미함, det EA는 (det E)(det A)와 동일함
  

• $E_1$은 interchange, $E_2$는 second row k scaling

• $E_3$은 second row에 k scaling한 것을 first row에 더한 replacement

• $E_4$는 first row에 k scaling 한 것을 second row에 더한 replacement를 의미
  

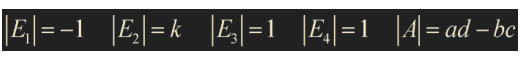
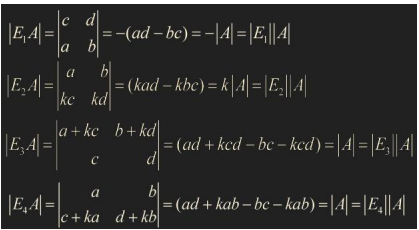
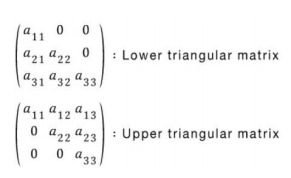
삼각행렬 행렬식(Triangular matrix determinatnt)

• A가 삼각 행렬이면 det A는 A의 diagonal term을 곱한 것
• det A = $𝑎_{11}𝑎_{22}𝑎_{33}$
  

8) 행렬식 성질

행 연산(Row Operation)

• A의 하나의 row 곱이 다른 row에 더해져 B 행렬이 만들어지면 det B = det A 임 이는 row replacement를 의미함

• B를 만들기 위해 A의 두개의 row가 interchange 됐으면 det B = -det A 임

• A의 하나의 row에 k가 곱해져 B가 만들어졌으면 det B = k det A 임 scaling을 의미

• a,b,c 세가지 성질을 이용하여 row reduction을 통해 사다리꼴을 만든 후 cofactor expansion을 이용하면 det를 쉽게 구할 수 있음

• det EA = (det E)(det A)와 det E = 1, -1, k임

• B는 A 행렬에 row reduction을 사용하여 만들어진 사다리꼴 행렬이라고 가정하면 B=EA로 표현

• 사다리꼴은 triangular matrix이므로 각각의 diagonal term을 곱하면 det를 구할 수 있음
  

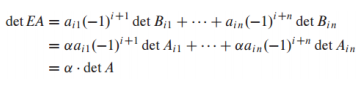
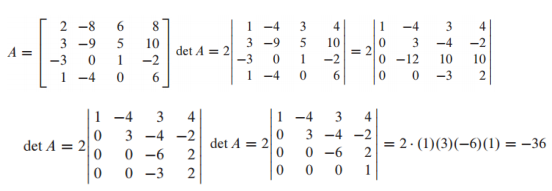
• cofactor expansion을 사용해서 determinant를 계산하면 n!의 연산이 필요함
• 하지만 row operation을 이용하면 $2𝑛^3/3$의 연산이 필요하므로 25x25이상의 행렬도 빠르게 계산

이론

• det A = 0이 아니면 A는 invertible 임

• A가 not invertible이면 det A = 0 임
  

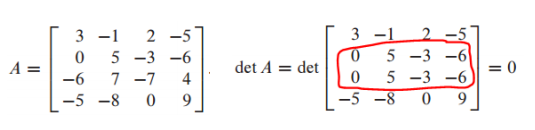
• $𝐴^𝑇$의 det와 det A는 동일함

곱셉의 성질(Multiplicatiove Property)

• det 𝐴𝐵 = (det 𝐴)(det 𝐵)
  

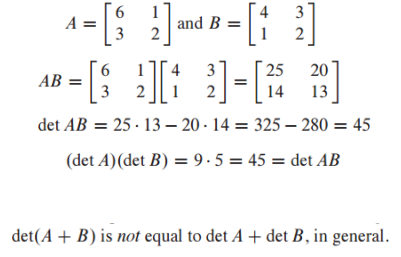
9) 고유벡터와 고유값

고유값과 고유벡터의 기본 idea

• 행렬 A, u, v가 다음과 같이 주어졌을 때 곱셈 결과를 시작적으로 표현
• Av의 경과는 동일한 line에 solution이 존재하도록 결과가 도출 됨
• 이것이 Eigenvalue와 Eigenvector의 기본 idea임
  

고유벡터(Eigenvector)

• 𝐴𝑥 = 𝜆𝑥를 만족하는 nonzero vector x가 eigenvector 임

• 또한, 𝐴𝑥 = 𝜆𝑥에서 x가 nontrivial solution(비자명해)이 존재할 때 scalar 𝜆가 eigenvalue가 됨

• 여기서 x를 𝜆에 상응하는 eigenvector라고 함

• 행렬 u와 v가 A의 eigenvector인지 판단하는 예시

• 𝐴𝑥 = 𝜆𝑥를 만족하는 확인하면 됨

• u는 A의 eigenvector, -4는 A의 eigenvalue가 됨

• v는 A의 eigenvector가 아님
  

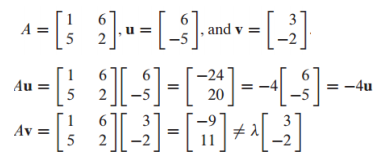
• 7이 A의 eigenvalue인지 파악하고 그에 해당하는 eigenvector를 찾는 문제

• x는 nonzero vector가 되어야 하고 이 식이 nontrivial solution이 존재하는지 파악하면 됨

• nontrivial solution을 파악하기 위해 zero vector를 포함한 augmented matrix를 row reduction 후에 free variable이 존재하는지 파악하면 됨

• $𝑥_2$ 가 free variable이고 $𝑥_2$ 로 표현한 general solution 은 아래와 같음

• nontrivial solution이 존재하므로 7은 A의 eigenvalue가 성립
  

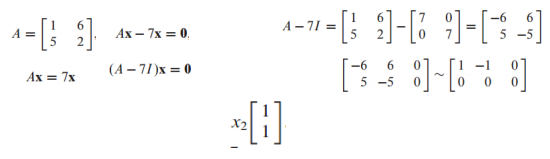
고유공간(Eigenspace)

• 𝜆가 A의 eigenvalue이면 (A- 𝜆I)x = 0은 nontrivial solution을 갖음

• 𝜆에 해당하는 A의 eigenspace는 A - 𝜆I 행렬의 null space를 의미 함

• eigenspace는 zero vector와 𝜆에 해당하는 eigenvectors 두가지를 포함함

• zero vector는 eigenvector에 포함되진 않지만, eigenspace에 포함 됨
  

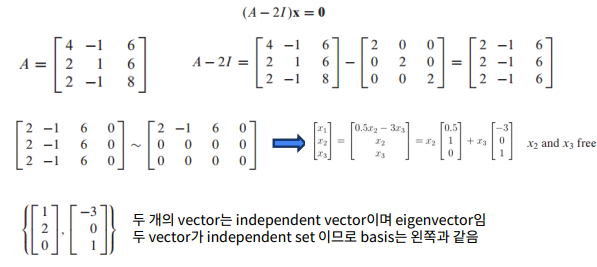
• 행 A가 다음과 같이 주어졌을 때 𝜆=2에 해당하는 eigenspace를 찾고 basis를 찾는 예시
  

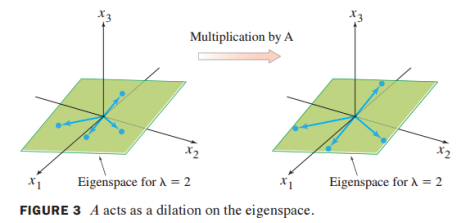
행렬 A에 의한 곱셈(Multiplication by A)

• 3차원 공간에 𝜆=2에 대한 eigenspace가 주어졌다고 가정함
• eigenspace는 zero vector와 eigenvectors를 포함함
• eigenspace에 존재하는 임의의 vector 4개를 선택해서 행렬 A를 곱하면 크기가 2배 씩 늘어나게 됨
  

이론

• triangular matrix의 eigenvalues는 diagonal term임

(1) A가 upper triangular matrix인 경우 A- 𝜆I는 아래와 같음 - 아래 방정식에서 nontrivial solution이 존재해야 함

• free variable이 존재한다는 것을 의미하므로 pivot position이 0이 되어야 함
• 따라서 𝜆는 $𝑎_{11} , 𝑎_{22} , 𝑎_{33}$이 될 수 있음
• 𝜆의 개수는 n개 이하가 되어야 하므로 3개 이하가 되어야 함

(2) A가 lower triangular matrix인 경우

• A와 $𝐴^𝑇$ 가 동일한 eigen value를 갖고 있다는 것을 증명하면 됨

• 𝜆I가 diagonal term만 존재하므로 다음의 식이 성립함
  

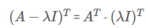
• A 행렬을 transpose하여도 diagonal term은 변하지 않으므로 A와 𝐴𝑇 가 동일한 eigen value를 갖음

이 글은 제로베이스 강의 자료 일부를 발췌하여 작성되었습니다