👉 오늘 한 일

• weekly 키워드 정리
• Tableau 설치
• 6주차 titanic 과제
• 인공지능 세미나 - 정형 데이터를 다루는 머신러닝 문제해결 패턴

weekly 키워드 정리

노션 페이지
https://www.notion.so/likelion-aischool/11-095bdd21d5334182bdf48e1568bcab9c

지도학습이란 ?

• 머신 러닝의 한 분야로, 데이터에서 반복적으로 학습하는 알고리즘을 사용하여 컴퓨터가 어디를 찾아봐야 하는 지를 명시적으로 프로그래밍하지 않고도 숨겨진 통찰력을 찾을 수 있도록 하는 데이터 분석 방법이다.

알고리즘 종류

지도학습 알고리즘 중 5개만 선택

K-최근접 이웃(k-Nearest Neighbors)

1. K-최근접 이웃 알고리즘 ?

• 주변의 가장 가까운 K개의 샘플을 통해 값을 예측하는 방식

• 이미 각 데이터의 분류를 알고 있으면 새로운 데이터가 등장했을 때 새로운 데이터를 어디로 분류할지 정할 수 있다.

• 가장 간단한 머신러닝 알고리즘으로, 분류와 회귀 모두 사용할 수 있다.

2. 예시

• 하얀 점 = 분류가 안 된 새로운 데이터, 빨강이나 초록으로 분류하는 알고리즘이라면?
  

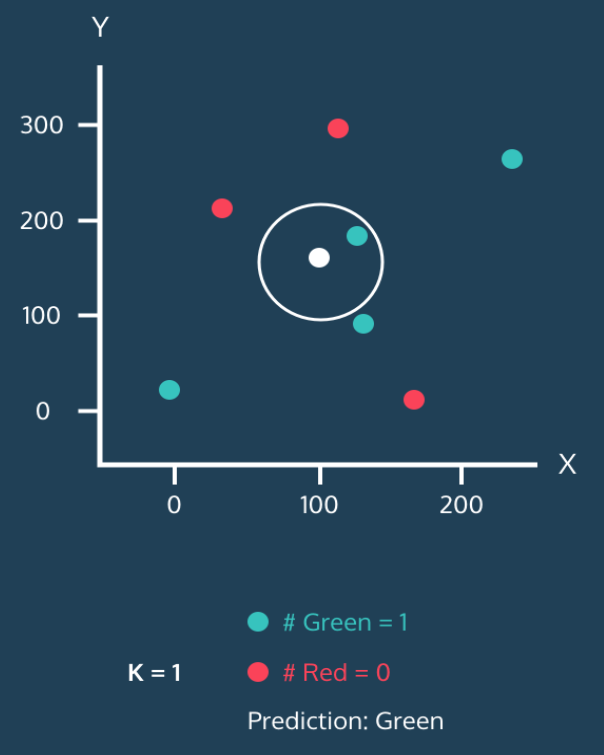
• k=1, 하얀 점은 초록으로 분류됨

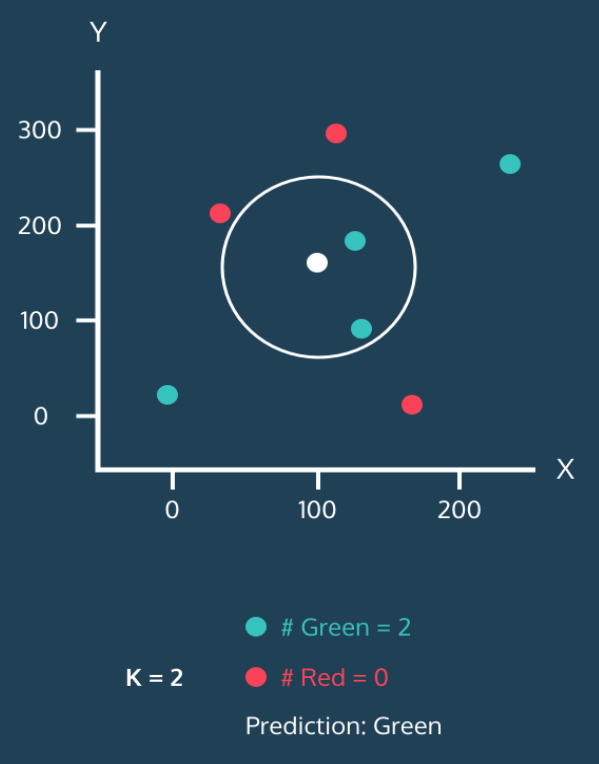
• k=2, 하얀 점은 초록으로 분류됨
  

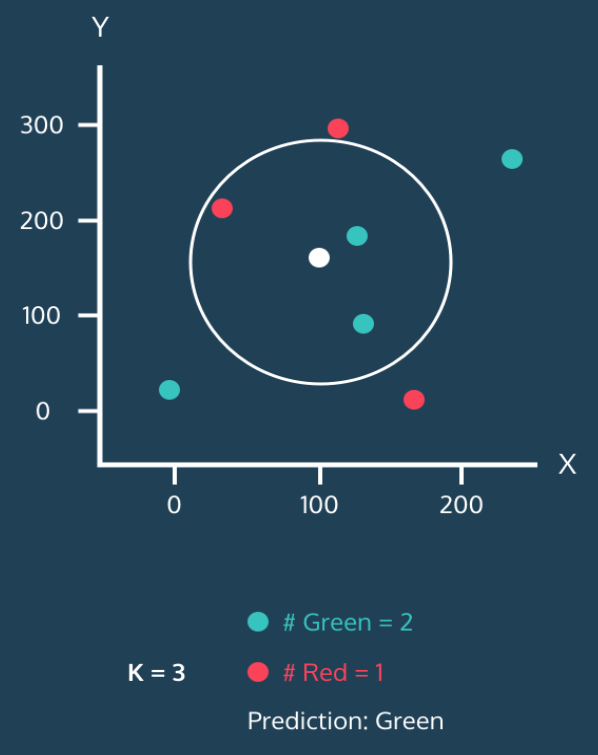
• k=3, 주변에 초록 2 , 빨강 1이므로 초록으로 분류됨
  

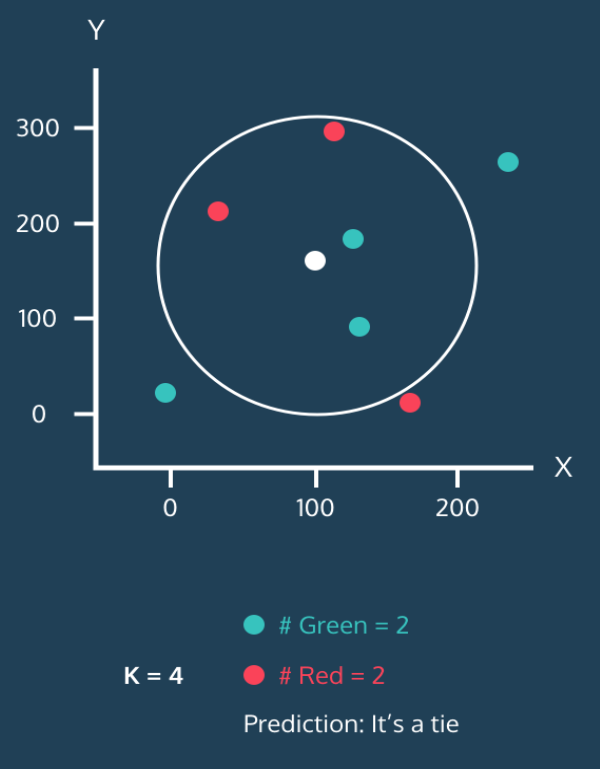
• k=4, 원 안에 초록2, 빨강2
• 이를 처리할 때는 가장 가까운 이웃을 따른다던가, 랜덤으로 처리함 but, 실제 데이터가 충분하면 거의 발생하지 않음
  

K-최근접 이웃 회귀

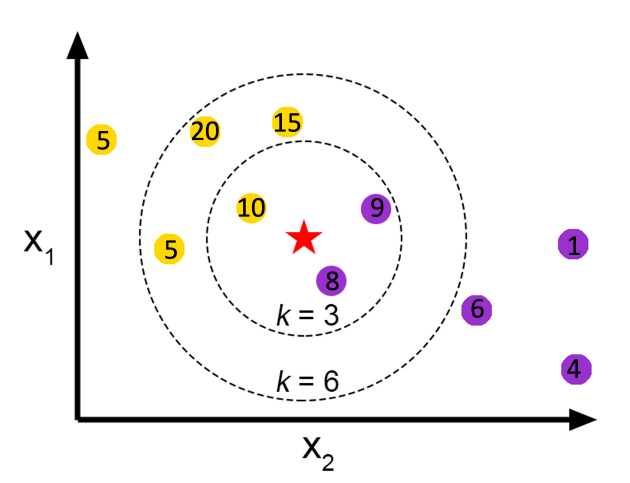
• '새로운 데이터 X(별표)가 주어졌을 때, X에 가장 가까운 K개의 데이터 값을 평균내서 값을 예측하는 것'
• 빨간별의 위치에 있을 데이터 값은 (10+9+8)/3의 결과값인 9로 예측된다.
  

3. 장점
   1. 이웃 샘플들의 값을 토대로 타깃값을 예측하여 직관적으로 추론이 가능하며, 극단적인 값의 영향을 적게 받음
   2. 구현하기 쉽고, 알고리즘을 이해하기 쉽다.
4. 단점 :
   1. 이상치 샘플을 제대로 예측할 수 없음(극단적인 값이어도 항상 일정하게 예측한다.)
   • K가 너무 작을 때 : Overfitting(과적합)
   • K가 너무 클 때 : Underfitting(과소적합)
   2. 훈련 세트가 크면 예측이 느려진다.(데이터가 아주 많은 경우에 사용하기 어려움)
   3. K-최근접 회귀에서, 데이터 범위 밖의 새로운 데이터는 예측이 불가능하다.

선형 회귀(Linear Regression)

• Docs (단순선형회귀 → • 1.1.1. Ordinary Least Squares)
  1.1. Linear Models
  

1. 선형 회귀란?

• 선형회귀는 하나 이상의 피처와 연속적인 타깃 변수 사이의 관계를 모델링 하는 것
• 연속적인 label 값을 예측하는 것
• 특성이 하나인 선형 모델 공식(단순회귀)
  • Y = W0 + W1*X
  • where W0 : y축 절편, W1 : 특성의 가중치
  • 다중선형회귀는 Y = W0 + W1X1 + W2X2 … 이런식
  • ✔ 목적 : 특성과 타깃 사이의 관계를 나타내는 선형 방정식의 가중치(W)를 학습하는 것

2. 선형 회귀 모델의 평가 방법
   

2.1. MSE (Mean Squared Error)

$MSE = \frac{1}{n} \displaystyle\sum_{i=1}^{n} (y_i-\hat y_i)^2$

• 실제값과 예측값의 차이인 잔차들의 제곱 평균으로 정의
• 제곱을 해주기 때문에 이상치(outlier)에 민감
  

2.2. MAE (Mean Absolute Error)

$MAE = \frac{1}{n} \displaystyle\sum_{i=1}^{n} (\vert y_i-\hat y_i \vert)$

• 잔차들의 절댓값 평균
• MSE보다 이상치에 덜 민감
• 작을수록 우수한 모델

2.3. RMSE (Root Mean Squared Error)

$RMSE = \sqrt {\frac{1}{n} \displaystyle\sum_{i=1}^{n} (y_i-\hat y_i)^2}$

• MSE에서 제곱근을 취해준 형태
• 실제값과 비슷한 값으로 변환하기 때문에 해석이 쉬워짐
• 작을수록 우수한 모델
  

2.4. $R^2$(결정 계수), r2_score

$R^2 = 1- \frac {SSR}{SST}$

• SST 중 회귀 모델에 의해 감소된 부분의 비율
• SST(Sum of Squared Total) = 실제값과 평균과의 차이를 제곱한 것의 합

$SST = \displaystyle\sum_{i=1}^{n} (y_i-\bar y_i)^2$

• SSR(Sum of Squared Residual) = 잔차 제곱 합
  

$SSR = \displaystyle\sum_{i=1}^{n} (y_i-\hat y_i)^2$

• 종속변수에 대한 모델 설명력을 나타내는 척도로 사용
• 1에 가까울수록 설명력이 높다
  

이 외에도 huber loss, poisson, quantile 등이 있음

3. 가중치 추정하기 - 최소자승법(Ordinary Least Squares)

• 잔차제곱합을 최소화하는 방법으로 가중치 추정
• 즉, SSR를 최소화하는 방법
  

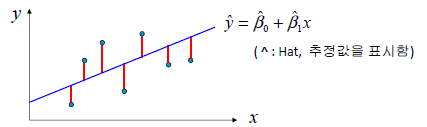
1. scikit-learn example

• 샘플 코드
  

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
    
# Load the diabetes dataset
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)
    
# Use only one feature
diabetes_X = diabetes_X[:, np.newaxis, 2]
    
# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
    
# Split the targets into training/testing sets
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]
    
# Create linear regression object
regr = linear_model.LinearRegression()
    
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
    
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
    
# The mean squared error
print("Mean squared error: %.2f" % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print("Coefficient of determination: %.2f" % r2_score(diabetes_y_test, diabetes_y_pred))
    
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color="black")
plt.plot(diabetes_X_test, diabetes_y_pred, color="blue", linewidth=3)
    
plt.xticks(())
plt.yticks(())
    
plt.show()

• Output
  

Mean squared error: 2548.07
Coefficient of determination: 0.47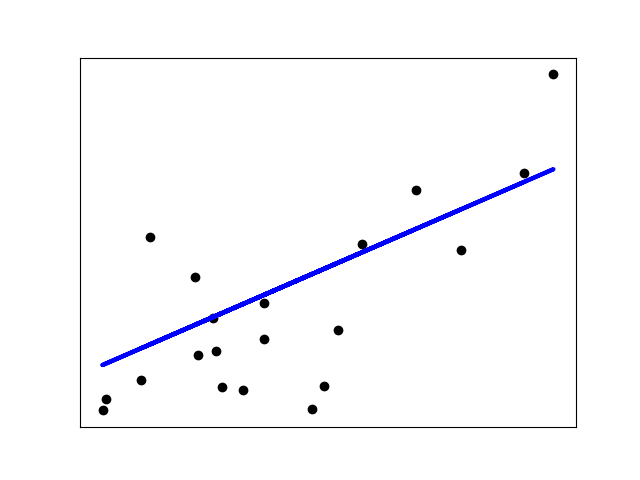

• Regularized regression model : Lasso, Ridge, Elastic Net 등

Tableau 설치

1. 홈페이지에서 DOWNLOAD TABLEAU PUBLIC 선택
   https://www.tableau.com/products/public/download
   

2. 항목 입력하고 설치
   

3. 설치파일 열고 항목 동의 후 설치
   

titanic 과제

groupby().agg()

• .agg()에 리스트 형태로 그룹별 적용할 agg func 지정 가능
• e.g.

df.groupby("deck")["fare"].agg(["count", "mean", "sum"])

• .agg()에 딕셔너리 형태로 그룹별로 컬럼마다 agg func 다르게 지정 가능 ->{컬럼 : 적용할 agg func} 지정
• e.g.

df.groupby(by=["class", "who"])[["age", "fare", "deck"]].agg({"age" : "mean", "fare" : "mean", "deck" : "count"})

인공지능 세미나 - 정형 데이터를 다루는 머신러닝 문제해결 패턴

머신러닝 문제해결 프로세스
1. 문제(경진대회) 이해

• 배경, 목적, 유형 등

  • 어떤 데이터를 활용해서 어떤 값을 예측해야 하는지?

  • 회귀인지, 분류인지?

  • 주어진 데이터가 무엇인지?

  • 어떻게 접근해서 문제를 풀어야 할지?

  • 배경지식, 사전지식을 사용할만한 점이 있는지?

• 평가지표 파악

2. EDA

• 데이터 구조 탐색, 몇 가지 통계값 구해보기

  • 제공된 파일별 용도 파악

  • 데이터 양(info, shape)

  • 피처 이해(이름, 의미, 데이터타입, 결측치, 고유값 개수 등)

  • 훈련 vs 테스트 데이터 차이(분포가 비슷한지, train에는 있지만 test에는 없는 피처가 있는지 등)

  • 타겟값 파악(train에 명확히 없는 경우도 있음)

• 데이터 시각화(중요 피처 탐색)

  • 다양한 그래프를 활용해 데이터 전반을 깊이있게 살펴봄

  • 이 과정에서 어떤 피처가 중요한지, 피처끼리 어떻게 조합해서 새로운 피처를 만들지, 어떤 점을 주의해서 모델링할지 인사이트를 얻음

3. 베이스라인 모델 구축

• 피처 엔지니어링
• 모델 훈련 및 성능 검증
• 결과 예측 및 제출

4. (성능이 만족스럽지 못할 시,) 성능 개선

• 피처 엔지니어링
• 하이퍼파라미터 최적화
• 성능 검증
• 결과 예측 및 제출