TSP란

입력으로 그래프. 사무실을 v1으로 나머지 v2 v3 v4는 내가 영업 뛰어야 하는곳.

• 어떤 순서로 가야 한번씩 방문하고 집에 돌아올까?

브루트 포스

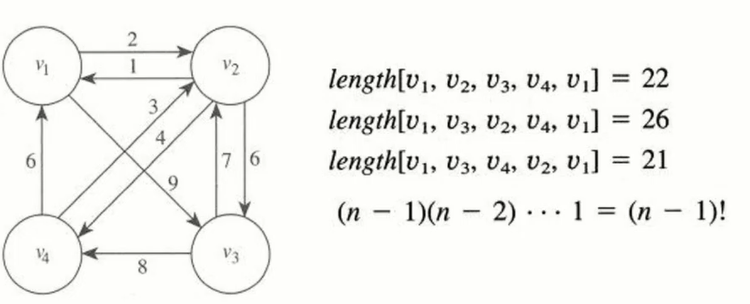
Worst case =>(n-1)(n-2)(n-3)...1 = (n-1)! = O(n!)

DP

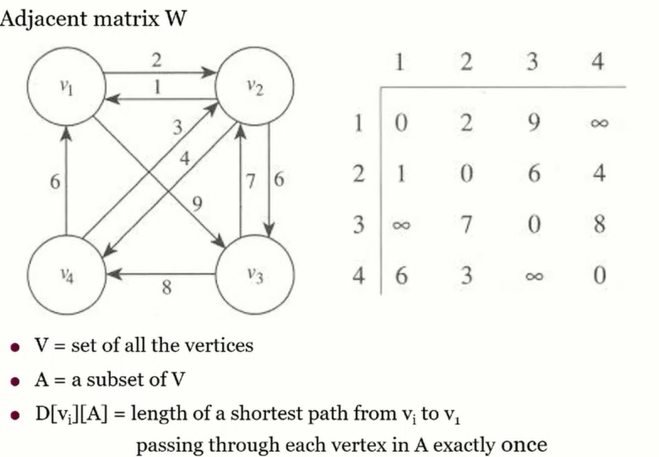
• 용어
  V: vertex의 집합
  A: 부분집합
  D: 로테이션 배열. vi는 출발지. vi~v1까지 가는 제일 짧은 length 를 D에 저장.

Ex)

• D[v2][A] 는 v2~ {v3,v4} 를 거쳐 v1에 도착하는 경로

점화식

• 부분문제를 사이즈가 제일 작을때까지 먼저 계산하고, 최종을 계산해
  

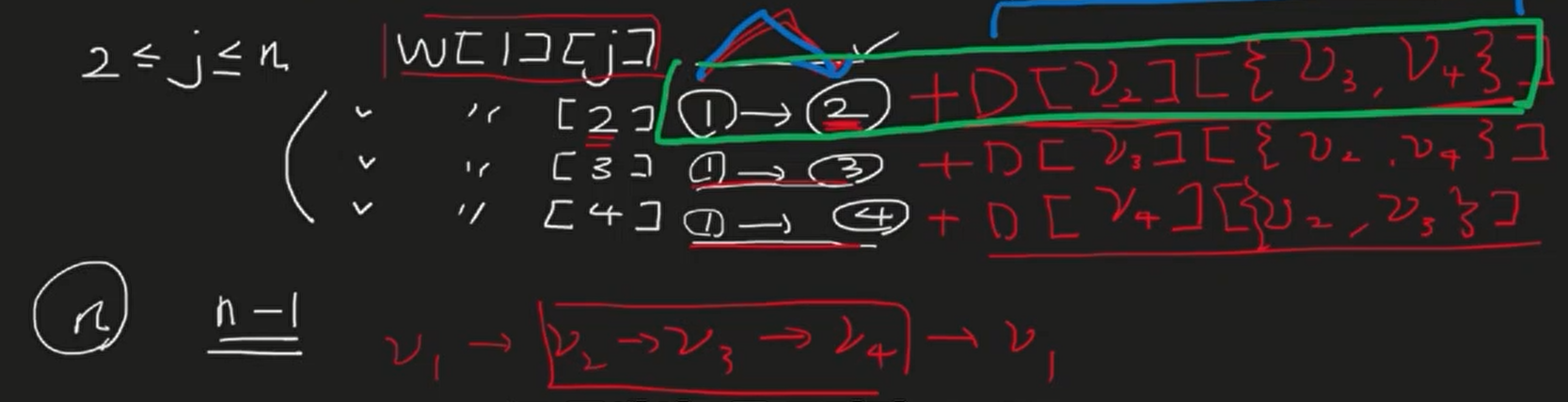
• v1->v2 일때는 v2->{v3,v4} 일때의 부분문제를 풀면되고

• v1->v3 일때도 v3->{v2,v4} 동일...

• 최종적으로 나온 v1->v2 , v1->v3, v1->v4 의 경우 중에 젤 작은걸 선택!

출발지가 1인경우는 최종 밖에 안돼.
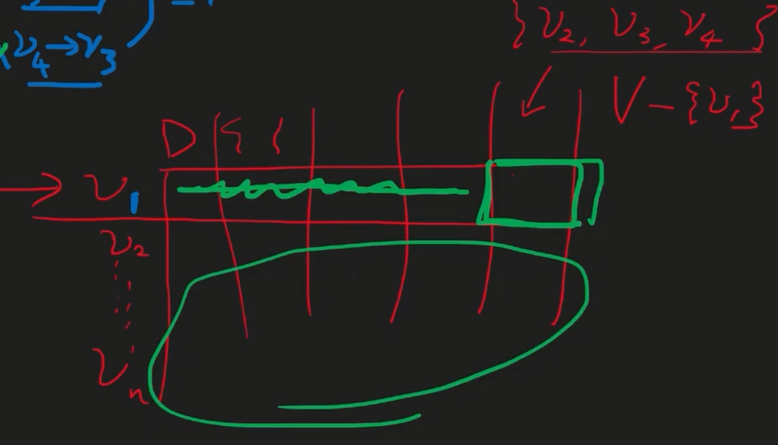이런 경우
부분문제에서는 나올 수 없어

부분집합에서 D[vi][A]. A에서는 i가 한번 나왔으니까 i 가 절대 나오지 않아

D[vi][A] = min(W[i][j] + D[vj][A-{vj}]) i~j까지는 왔으니까vj에서 출발. 풀려고 한 A에서 한놈은 방문했으니 후보가 A- vj(방금방문) 까지 가야해

Ex)


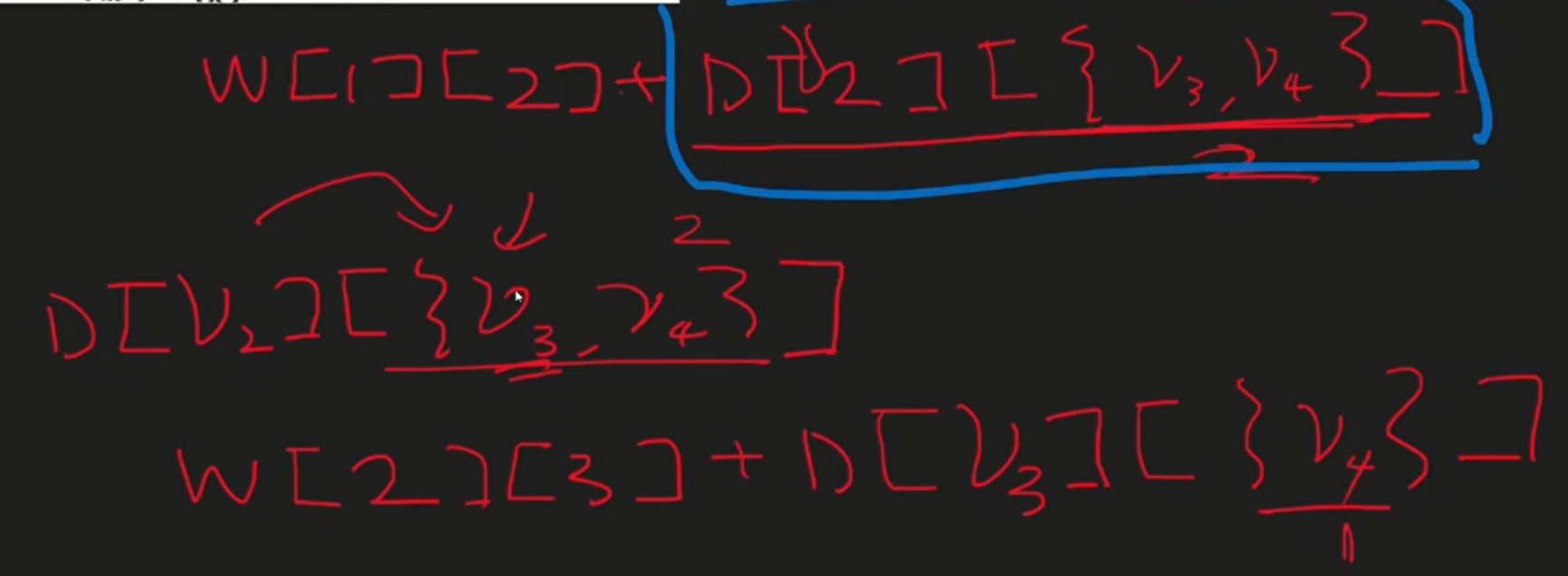
이렇게 연쇄적으로 DP

수도코드

• P 배열을 가지고 경로를 출력
• D[i][A]를 계산했을 때 j값을 P에 넣음. 이는 i~A 까지 애들중에 첫번쨰로 j 방문할게! 를 P에 저장해놓은거

Ex) P사용 방법

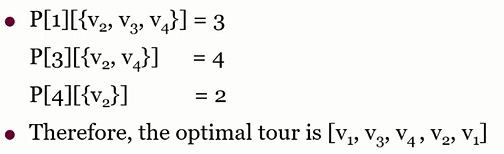
• D배열을 채워야해!
  
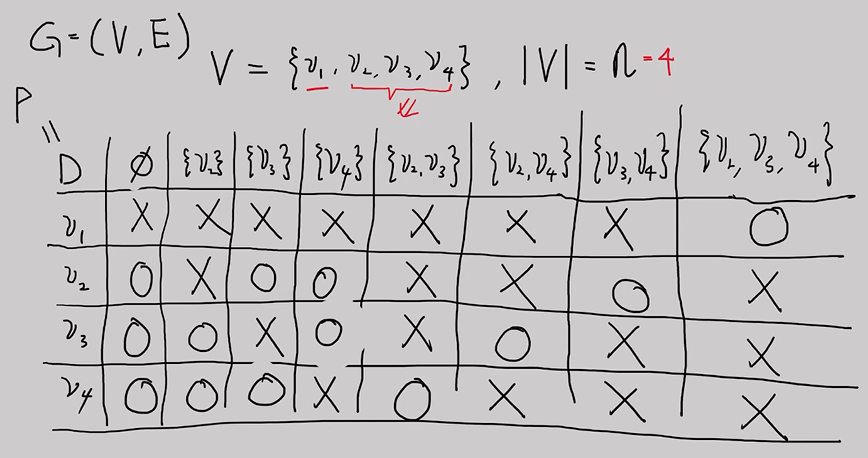
• 경로를 따지지 않아, DP는 오직 W+D만 할뿐
  규칙)
• 열인덱스에 있는 놈은 행인덱스에서 빼고 계산
• 행인덱스가 v1은 최종문제만 계산

A 원소의 개수가 0일때, 1일때, 2일때, 3일때 파악

• 열 인덱스가 다 공집합
  
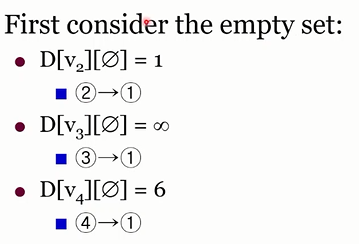
  vi -> v1 인경우니까 W[i][1]

• 원소의 개수가 한개
  
  D배열을 참조하게 되어있고, D배열은 자기보다 한개 적은 배열(원소의 개수가 0개인 위에 그림) 을 참조!
  W+D 한번만

-A 원소의 개수가 두개

여기서는 또 D배열이 원소의 개수가 1개인 위에 그림을 참조!
W+D 2번

• 원소의 개수가 세개
  
  얘 또한 원소의 개수가 2개인 위에 그림을 참조!
  W+D 3번

...최종 A의 사이즈가 n-1개 까지 가서 마지막 문제(min(W[1][j]+ D[vj][V-{v1,vj}])를 푼다!

성능분석

• 가장 많이 도는 부분에서 3중 for 문 안에 min(W[1][j]+ D[j][A-(vj)]) 이 Baisc Operation

• 가장 바깥 부분은 A의 사이즈를 결정 (k는 A의 사이즈)
  ex) 여기서는 n-2번 돌아

• 두번째 for문은 A라는 집합을 각각 만들어줘야해
  ex) 여기서는 조합 (n-1)C(k)

• 세번째 for문은 구체적인 i를 결정해줘(i는 v1이 될 수 없고 A안에 있으면 안돼)
  ex) A의 원소의 개수는 k임으로 여기서는 n-1-k 번 돌아

• 마지막 min은 A라는 집합의 원소가 3개면 min은 W+D가 3개가 나와
  ex) 여기서는 k번 돌아

• k를 모두 더하면
  

• 조합을 꺠려면 이 공식을 이용
  

n-2를 보정한다음 계산

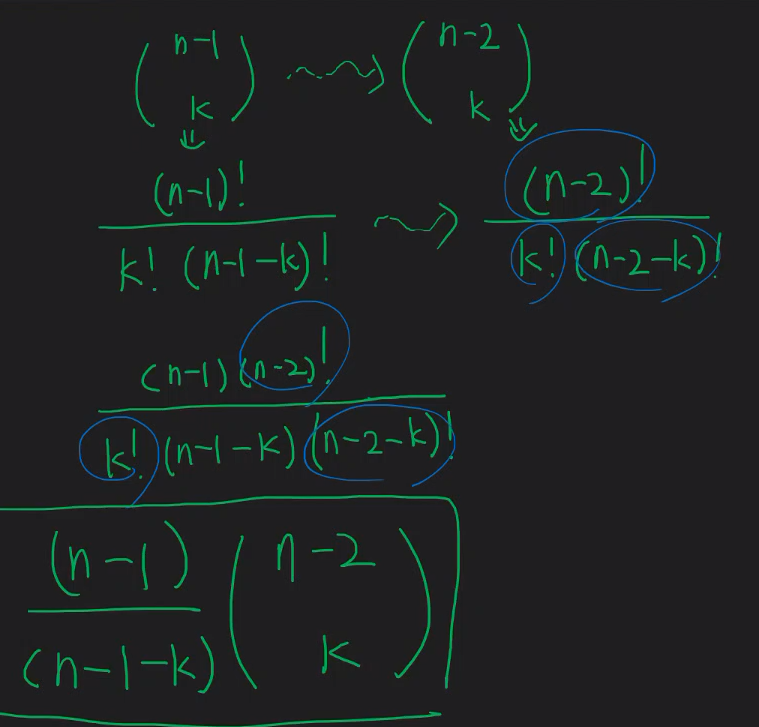
최종

따라서 O(n^2 * 2^n)

공간 복잡도

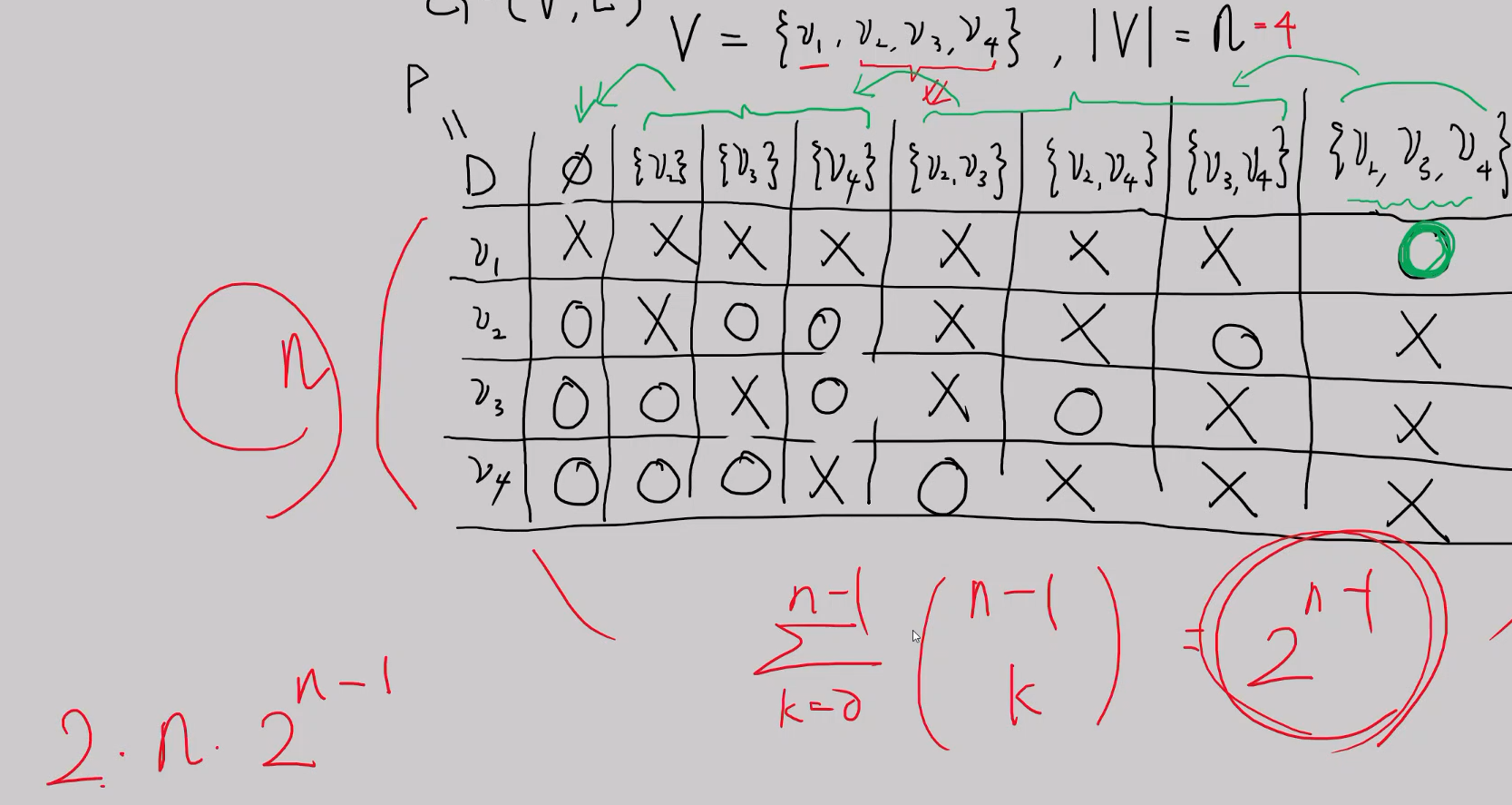
D배열 뿐만아니라 똑같은 P배열도 있으니 O(n2^n)