BFS

개념

• 시작 정점으로부터 가까운 정점을 먼저 방문하고 떨어져있는 정점을 나중에 방문
• 깊게 탐색하기 전에 넓게 탐색
• 방문한 노드들을 차례대로 저장할 수 있는 큐(Queue) 를 사용

BFS 알고리즘

BFS(G)

• 초기화 작업은 DFS와 동일
  • 그래프 G의 모든 vertex와 edges 들에 대해 setLabel() 을 호출해서 UNEXPLORED 으로 초기화

BFS(G,s)

• Li : 시작정점으로 부터 거리가 i인 정점들의 집합 (시퀀스)

1) 새로운 시퀀스 L0 에 시작정점을 삽입하고, VISITED 처리한다.

2) Li 가 비어있지 않을때까지 아래 루프를 반복한다.

• 새로운 시퀀스 Li+1 을 생성한다.

• Li 에 저장된 정점의 인접 간선(incident Edge) 에 대해 UNEXPLORED 인지 조사한다.

  • UNEXPLORED 이면 간선의 반대 정점도 UNEXPLORED 인지 조사한다.

  • UNEXPLORED 이면 간선은 DISCOVERY 로, 반대 정점은 VISITED 로 설정하고 Li+1 에 반대 정점을 삽입한다.

  • UNEXPLORED 아 아니면 해당 간선을 CROSS 로 설정한다.

3) i를 1증가시킨다.

예시

• 큐에서 dequeue 되는 vertex 에 대해서 incidentEdges 들을 확인한다.

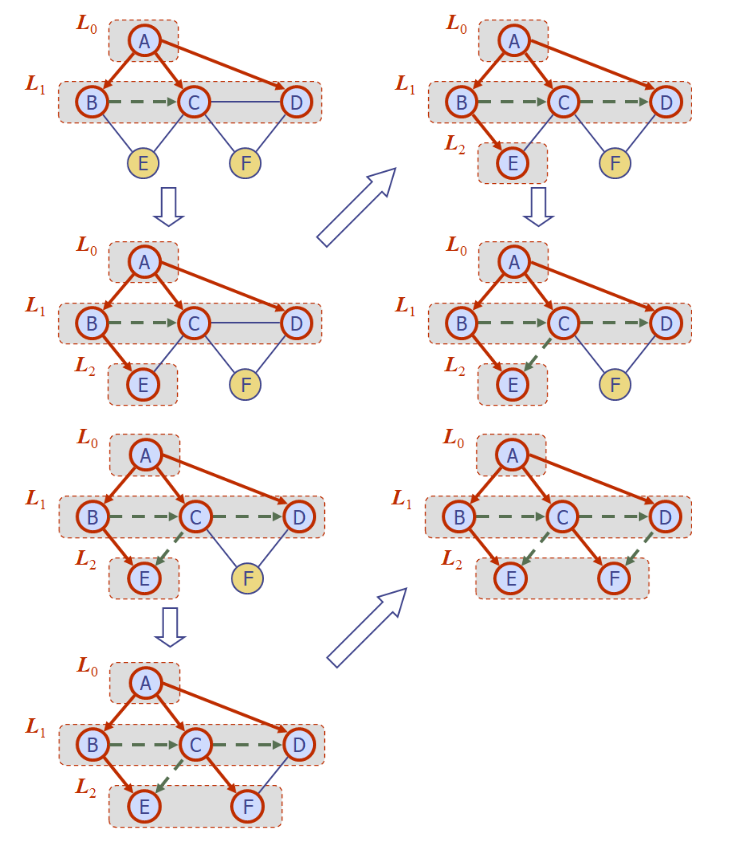
성능분석

• 한 정점에 대해 수행하는 작업들 : O(deg(v)) + O(1)

  • O(deg(v)) : Li 에 감긴 하나의 간선에 대한 방문처리와, 해당 간선의 반대쪽에 있는 정점에대해 방문처리를 하는 작업이 O(deg(v)) 가 걸린다.

  • O(1) : 간선과 반대쪽(opposite(v)) 정점의 상태가 모두 UNEXPLORED 이면 방문처리 하는 추가작업이 수행된다.

=> 즉, 간선들에 대해 방문처리하는 작업은 O(deg(v)) 가 걸리고,
정점들에 대해 수행하는 작업은 O(1) 이 걸린다.

그래프의 정점의 갯수가 n 이고 간선의 갯수가 m 일때, 인접리스트로 구현되면 O(n+m) 시간에 거쳐 수행된다. 이때, DFS와 BSF모두 한 정점당 1 + deg(v) 만큼의 연산을 수행하므로,

Σ O(1)+O(deg(v)) = O(n) + O(2m) = O(n+m) 의 원리가 적용된다.