Digraph (Directed graph)
- 방향 그래프 (간선에 방향이 있는 그래프)
DAG (Directed Acyclic Graph)
- 사이클이 없는 방향그래프
- DAG가 갖는 가장 큰 특징은 Topological Order(위상 순서)가 있다는 것이다.
Topological order (위상순서)
- 나와 간선으로 연결되지 않은 정점인 경우, 나보다 순서가 먼저 나와도 상관X
- 나에게서 다음 정점으로 가는 간선이 있는경우, 그 다음 정점은 순서가 나보다 나중에 나와야하는 순서를 가진다.
예시
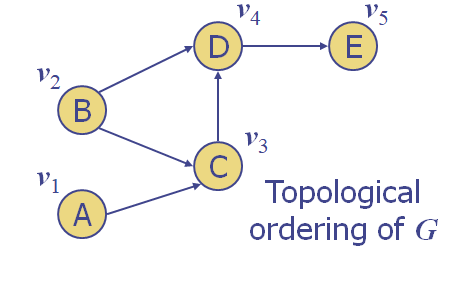
v1 에서 v2 로의 순서는 정해져도 상관x
=> 서로 순서가 관계없기 때문. 위상순서가 v1 과 v2 사이에는 정해져있지 않다.
하지만, v2 에서 v3 로의 순서는 반드시 v2 가 먼저, v3 가 나중이라는 순서가 정해져있다. (위상순서, 즉 선후수 순서가 정해져있기 떄문)
즉, 방문순서를 A-B-C-D-E 의 순서를 방문하는 것도 괜찮고,
B-A-C-D-E 순서로 방문하는 것도 괜찮지만,
C-A-B-D-E 또는 C-B-A-D-E 순서는 불가능하다!
ex. 선수-후수 과목
=> 사이클이 있는 방향 그래프인경우, 선수-후수 관계까 꼬일수있으므로 위상순서를 가지지 못한다! ( 자구-알고리즘 듣는 선후수 순서가 정해져있어야 하는데, 사이클 관계로 인해 알고리즘-자구 순서가 존재할 수도 있기때문)
Topological Sort (위상정렬)
- 위상순서에 맞게 그래프의 순서를 정렬하는 것
- incoming : 하나의 정점에 대해 들어오는 간선
- outgoing : 하나의 정점에 대해 나가는 간선
=> 이떄 outgoing 간선이 없는 정점을 기준으로 알고리즘을 작성 가능하다.

- 인풋 : 그래프 G : DAG / 아웃풋 : Topological Order
v : outgoing이 없는 정점
=> outgoing 이 없다는 것은 곧 자기 다음으로 작업해줄 정점이 없다는 것이니까 우선순위가 가장 뒤에있는 마지막 정점이라는 뜻!
-
v에다 순서 번호를 표시한다.
- ex. 정점 40개가 있을때, 맨 처음으로 찾아낸 outgoing 이 없는 정점 v가 40번째 순서로 방문하는 정점임을 표시하기 위해 40을 표시한다.
-
그래프 G 를 복사한 그래프 H 에서 해당 정점을 삭제한다.
- 정점을 지울떄 연결된 간선들도 같이 지워야하므로,
나한테 들어왔던 incoming 간선을 삭제한다. - 나한테 incoming 간선을 보낸 정점의 입장에서는 그 간선이 outgoing 간선일 것이다.
- 즉, 삭제된 정점의 바로 앞 순서를 가지는 정점도 outgoing 이 없는 정점으로 변하게 된다!
- 그렇게
- 정점을 지울떄 연결된 간선들도 같이 지워야하므로,
-
그렇게 새롭게 생긴 outgoing 이 없는 정점을 찾아나가면서, 즉 나의 바로 앞 순서를 가지는 정점들을 찾아내면서 방문 순서를 표시해준다!
(39 -> 38 -> 37 -> ... -> 2 -> 1)
위상정렬을 DFS 로 구현하기

예시
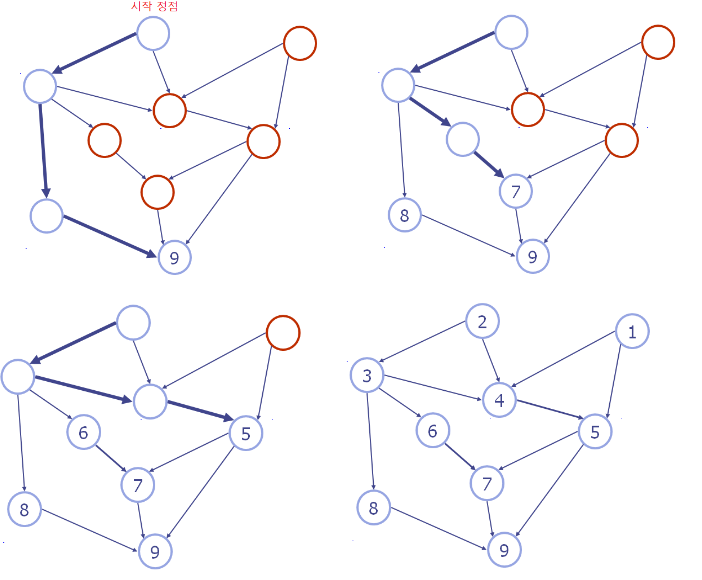
- 기존 그래프 G에서 outgoing 엣지가 없는 정점을 찾고 9를 넘버링 한다.
-
복사된 그래프 H에서 9가 넘버링된 정점을 삭제한다.
그에 따라 삭제된 정점을 향해있던 간선들 3개가 같이 삭제될 것이다. -
DFS 를 사용했으므로, DFS 특성에 따라 자기가 없어지면 (즉, 자기에 대한 작업을 다 마쳤으면) 자신을 호출했던 곳으로 돌아가는 재귀의 특성에 따라서 outgoing 간선이 없는 새로운 정점들중에 DFS 로 자신을 호출했던 정점으로 되돌아가서 8번으로 설정한다.
-
8 이 카운팅된 정점을 복사된 그래프 H 에서 삭제하고, 자신을 호출했던 정점을 확인해보니, outgoing 간선이 아직 남아있다.
(=> outgoing 간선이 아직 남아있는지 여부는 DFS 를 통해 알수있다 ) -
다른 정점 찾아보니 아까 넘버링 된 9 정점을 삭제할 때 outgoing 이 없어진 정점 2개가 남아있지 않는가? 이들에 대해 넘버링을 진행하면 된다.
-
7번 넘버링하고 그 정점 지우고 간선들을 지운다.
수행시간
- 위상정렬을 인접 리스트로 구현하면 O(n+m) 시간이 걸린다.