최단 경로 문제 중, 하나의 정점에서 다른 모든 정점까지 가는 데에 걸리는 최단 비용을 구하는 알고리즘이다. 다익스트라 알고리즘은 욕심쟁이 알고리즘과 비슷하다. 현재의 정점에서 갈 수 있는 모든 정점을 확인하고, 그중에서 가장 비용이 적은 정점을 선택해 최선의 선택을 하게 된다.
동작 방식은 BFS와 비슷하다. 현재의 정점에서 갈 수 있는 모든 정점을 힙에 넣고, 그중에서 가장 비용이 적은 노드를 선택해 가장 짧은 경로를 업데이트 해나가는 것이다.
다익스트라 알고리즘을 구현하는 자료구조는 우선순위 큐를 사용해도 되지만, 파이썬에서는 대부분 최소힙을 사용한다. (가장 상위노드에 가장 적은 값이 오는 구조)
1. 예시
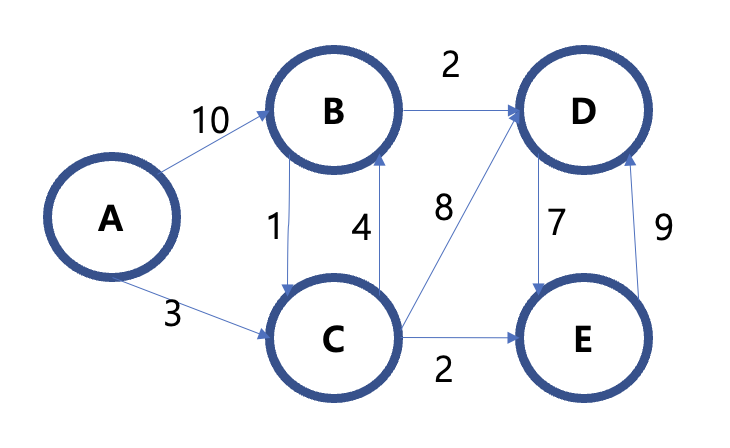
다음과 같은 그래프가 있을때, A에서 각 정점으로 도달하는 최소비용을 가진 경로를 구하라는 문제가 있다고 생각해보자.
2. 다익스트라 알고리즘 적용 방식
1) 정점간 최소 거리를 저장해야 하는데, 이때 시작 노드인 A에서는 0을 저장한다. 그리고 나머지는 무한대로 저장한다.
[0, ∞, ∞, ∞, ∞ ]
2) 우선 순위 큐(최소 힙)에 시작 노드 거리A의 거리인 0을 추가한다. 여기서 A의 거리란 A에서 A로 도달하는 거리를 말함으로 당연하게도 0이 된다.
3) 우선 순위 큐에서 최초로 넣은 0을 추출한다.
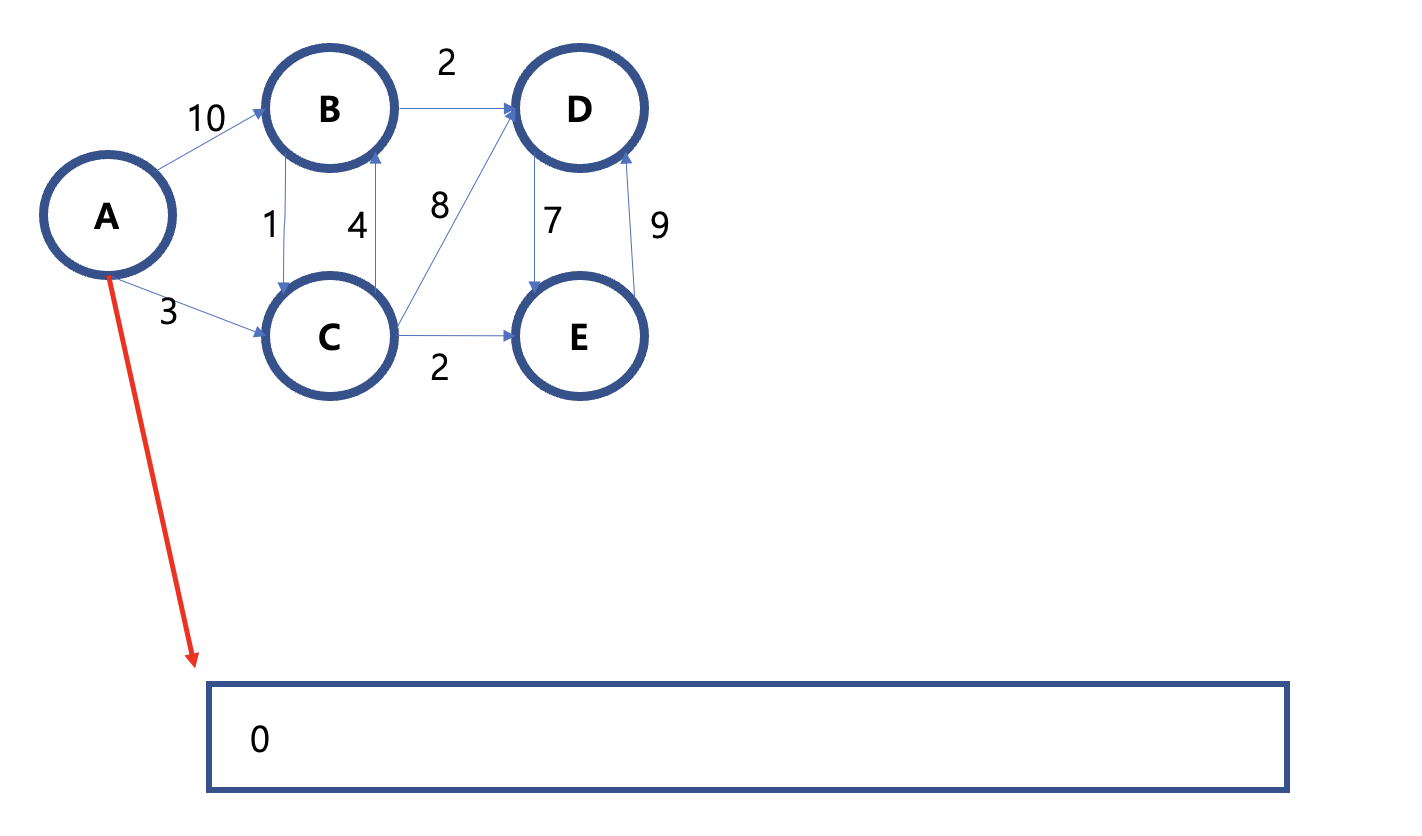
4) 추출된 노드A에서 이동할 수 있는 노드들의 거리와 배열에 저장되어있는 거리를 비교한다.
-> A에서 이동할 수 있는 노드는 B와 C이고, 정점간의 거리가 저장된 배열에는 A를 제외한 모든 노드가 무한대로 저장되어있음으로 B와 C사이의 거리도 무한대이다.
-> 따라서 B와 A, C와 A사이의 거리가 각각 무한대에서 10, 3으로 업데이트 된다. !!
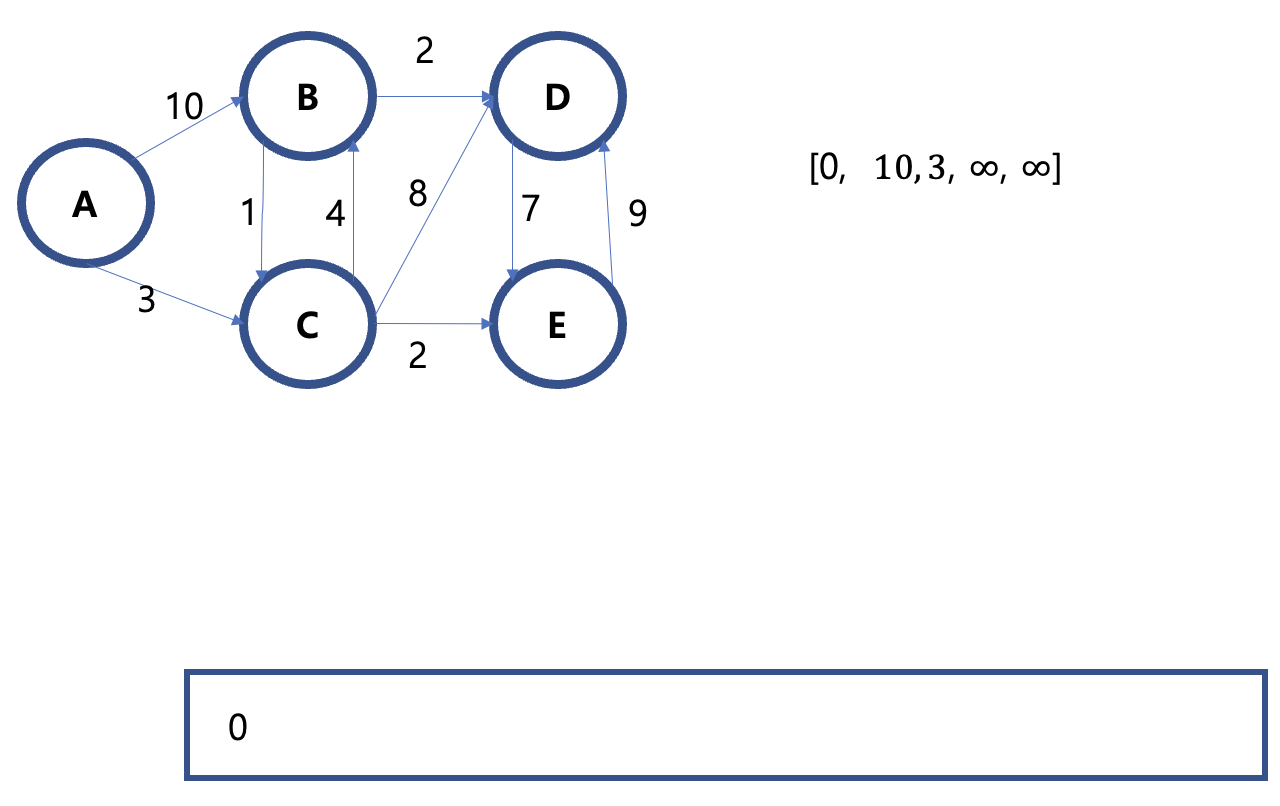
5) 이후, 배열에 데이터가 업데이트 되면 우선 순위 큐에 삽입한다.
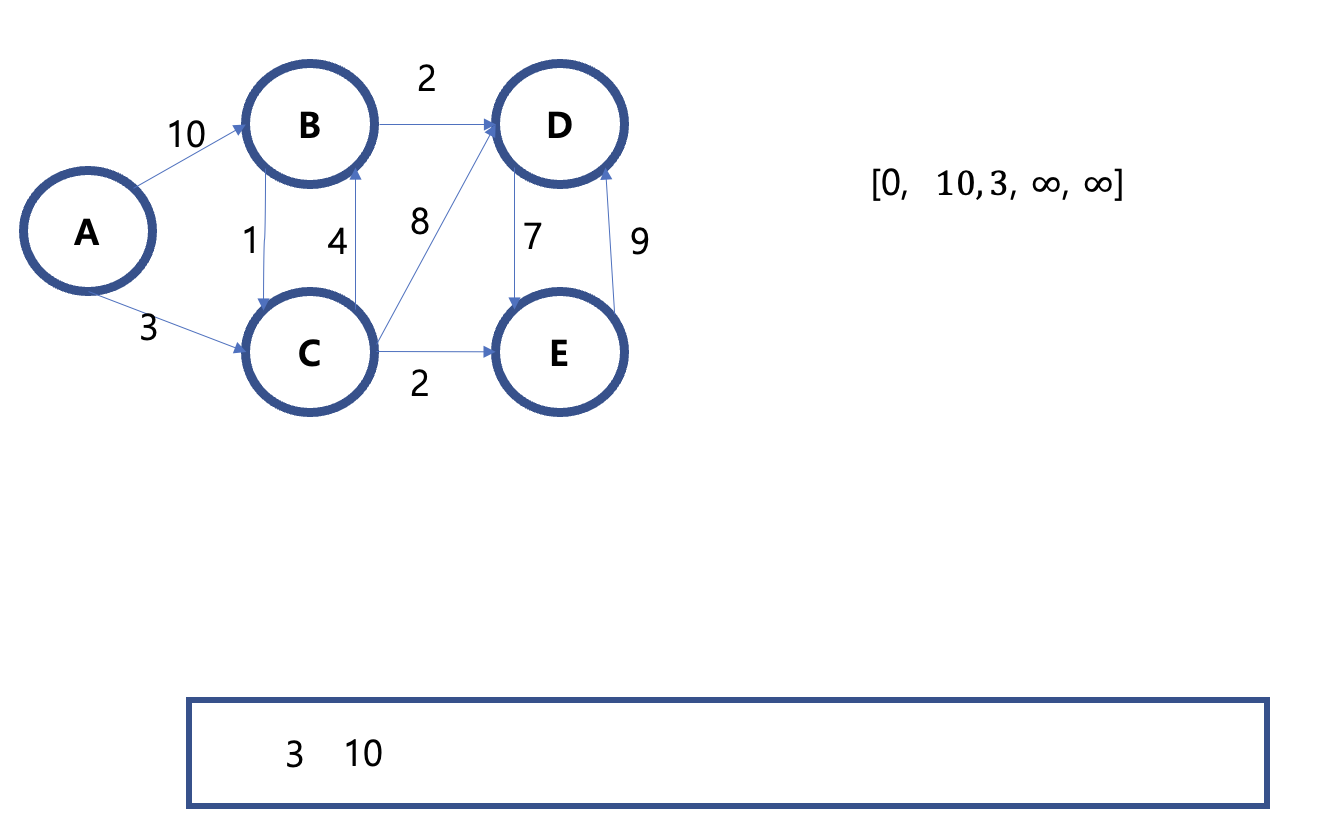
여기서 큐는 가장 값이 작은 원소가 가장 앞에 오도록 재정렬 됨으로, 3이 가장 앞에 오게 된다.
6) 이후, 우선 순위 큐에서 꺼낼 데이터가 없을때까지 반복한다.
여기서부터가 헷갈릴 수 있다. 여기서부터 잘 봐야 한다.
7) 우선순위 큐에서 가장 작은 원소인 3이 추출되고, 3과 연결된 노드 C에서 이동할 수 있는 노드들의 거리와 배열에 저장되어있는 거리를 비교하여 큐를 업데이트 한다.
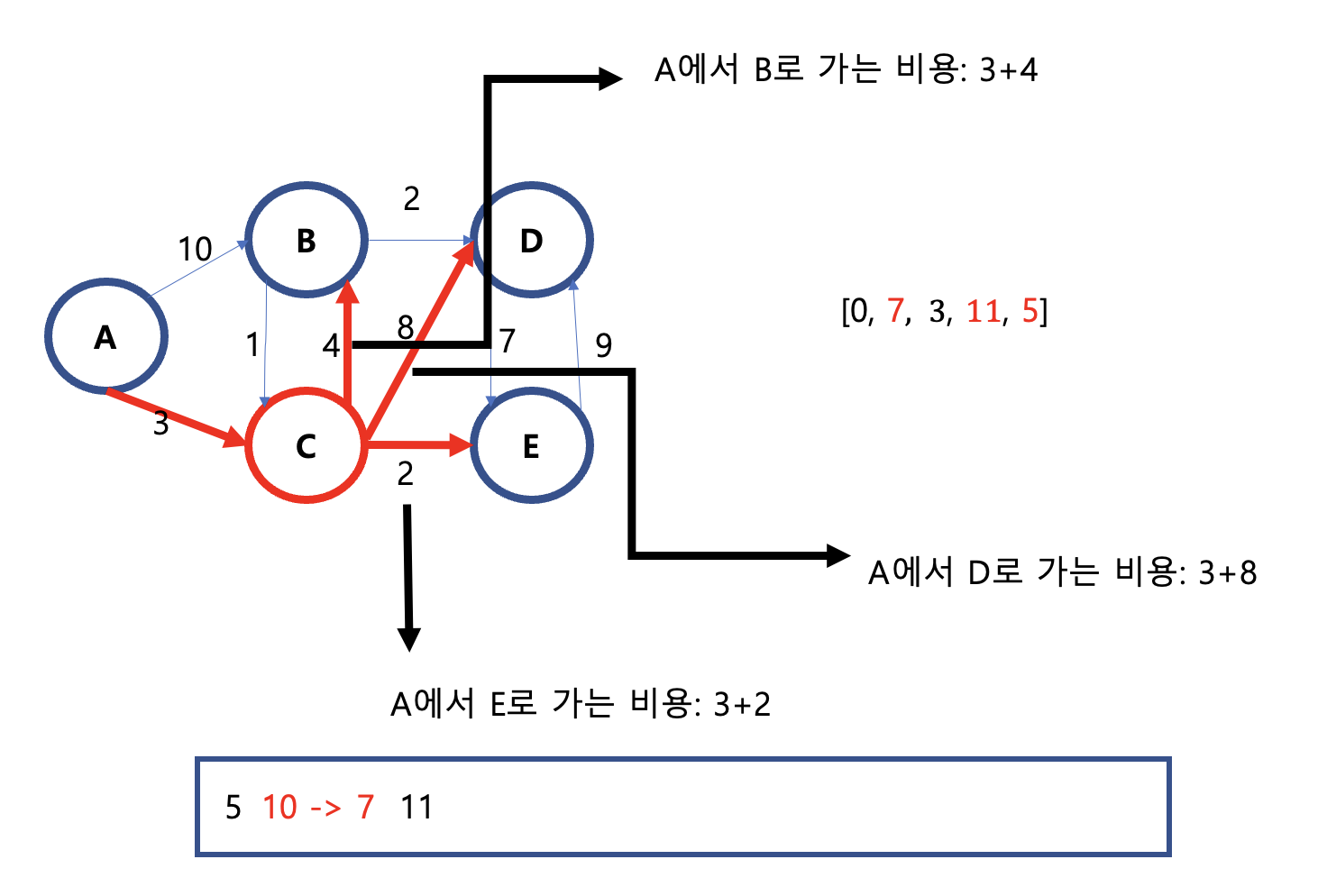
이때 거리를 비교하는 것이 무한대랑 4, 무한대랑 2, 무한대랑 8을 비교해서 교체하는 것이 아니다. 최초의 원소 A를 기준으로 진행된다.
• 제일 처음으로, A에서 B를 가는 비용은 10으로 되어있었으나, A에서 C를 거쳐 B로 가는 비용이 7로 더 적음으로, 10에서 7로 업데이트 한다.
• A에서 C를 거쳐 D를 가는 비용은 무한대로 되어있었음으로 11으로 업데이트 한다.
• A에서 C를 거쳐 E로 가는 비용은 무한대로 되어있었음으로 5로 업데이트 한다.
8) 다시 우선순위 큐에서 가장 작은 원소인 5가 추출되고, 5에 연결된 노드 D에서 이동할 수 있는 노드들의 거리와 배열에 저장되어있는 거리를 비교하여 큐를 업데이트 한다.
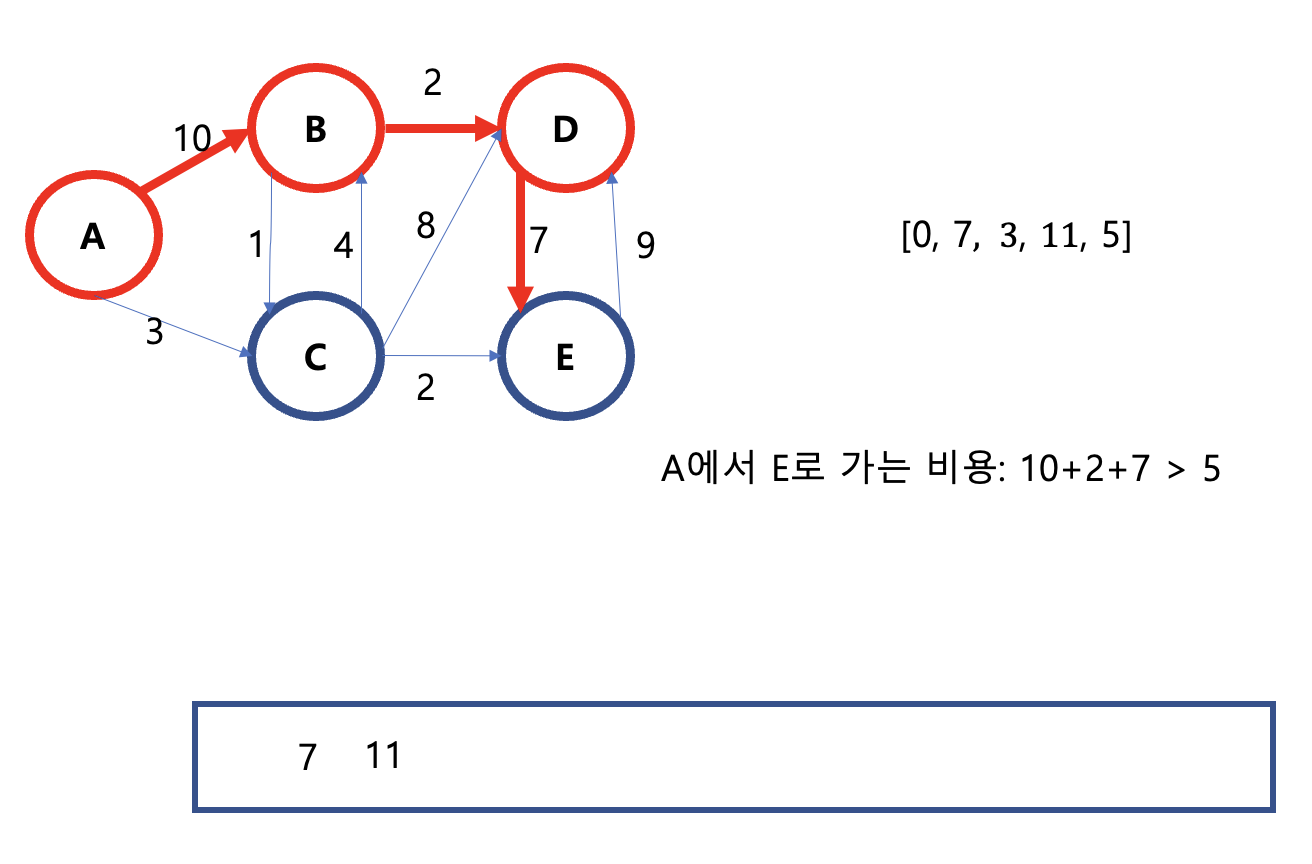
여기서는 A에서 E로가는 비용이 비교되는데 기존에 5보다 큼으로, 교체되지 않는다. 이후에는 나머지 큐에 있는 원소를 비교하게 된다.
9) 7에 연결된 노드인 B에서 이동할 수 있는 노드들의 거리와 배열에 저장되어있는 거리를 비교하여 다시 업데이트 한다.
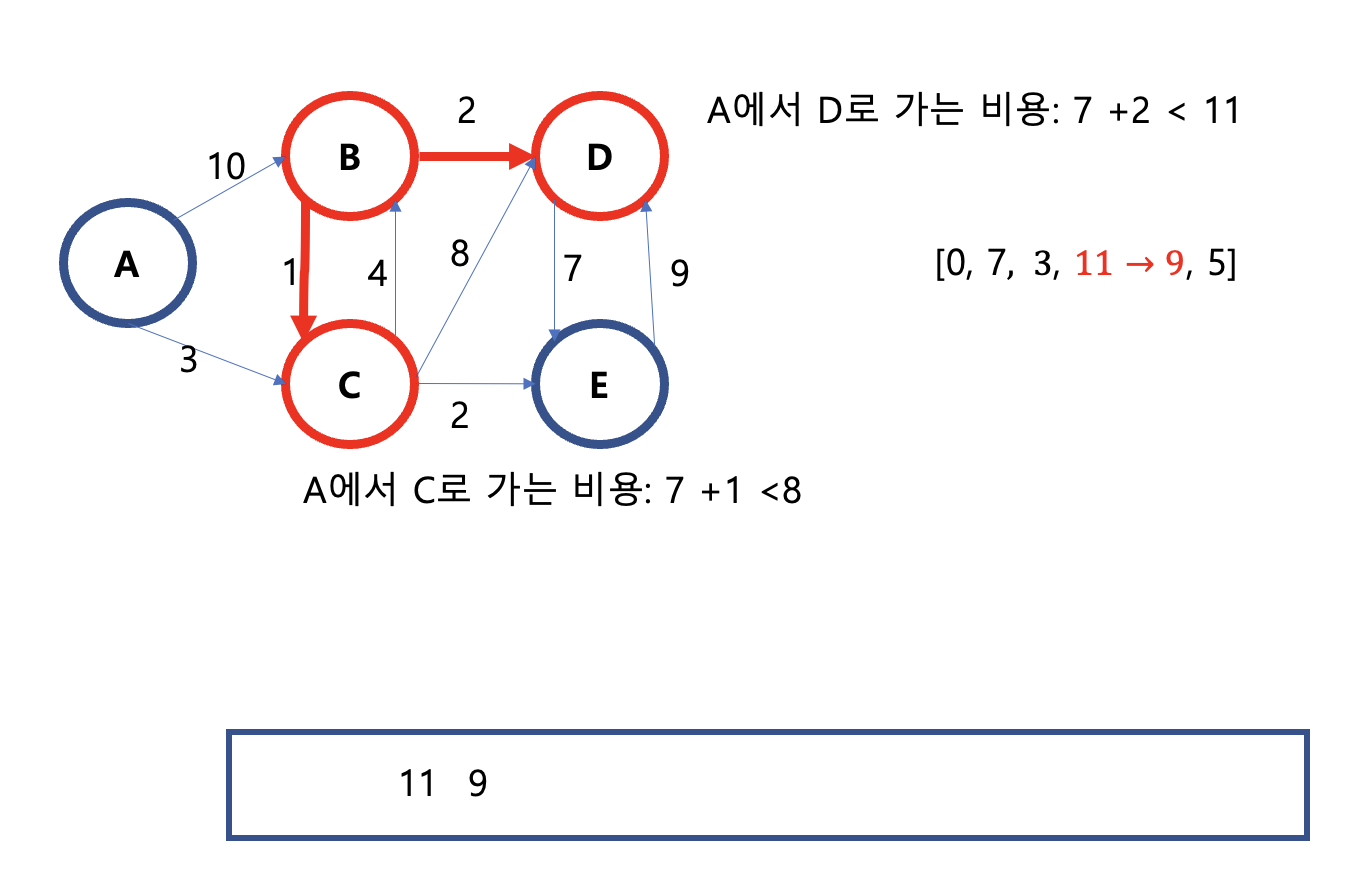
10) 이후 다시 동일한 비교 작업을 하지만, 이때 9에서 11로 교체된 거리는 큐에서도 삭제된다.
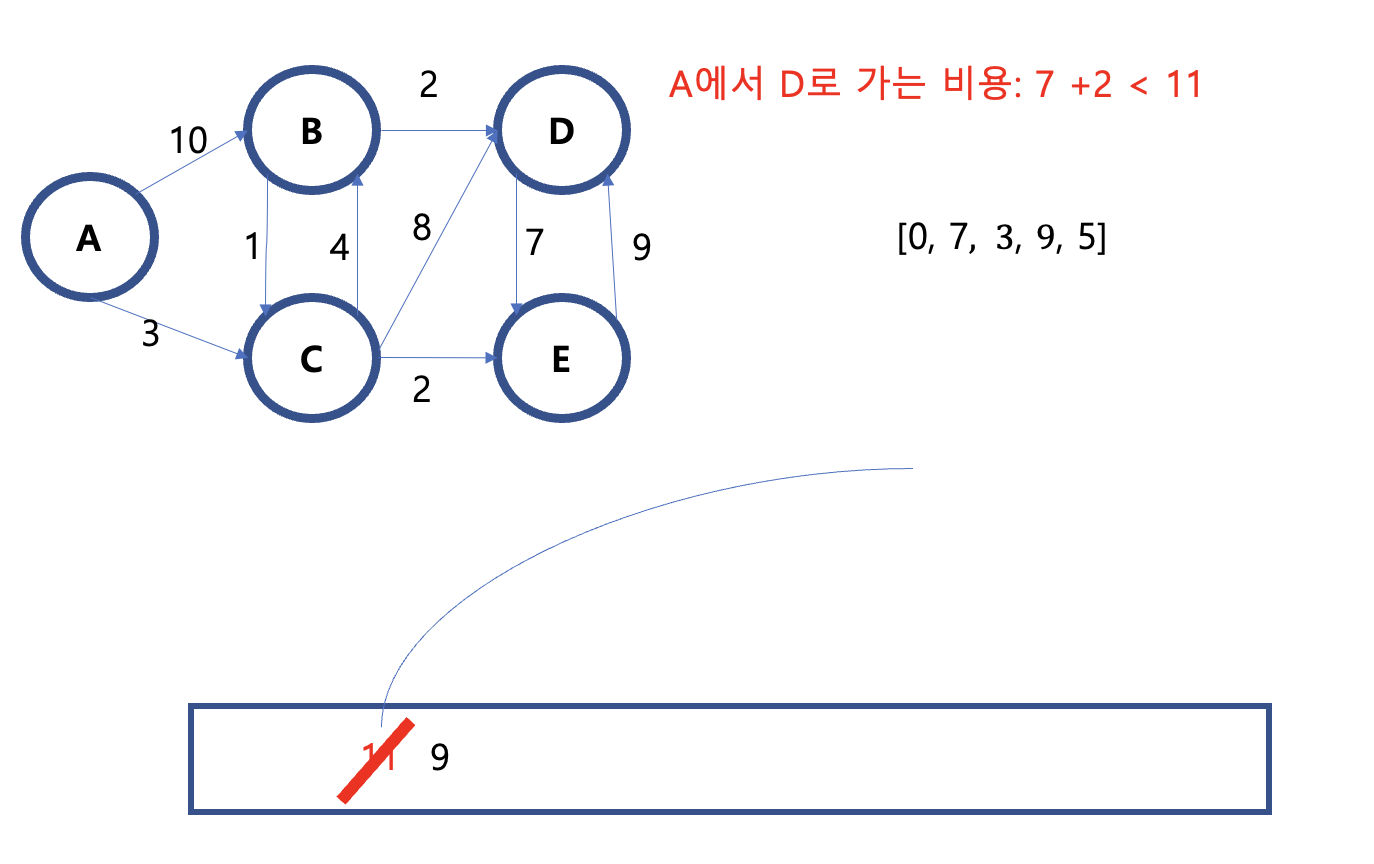
11) 최종적으로 다시 9에서 시작한다. A에서 D를 가는 비용은 앞선 정점들을 지나 9로 누적되어있다.
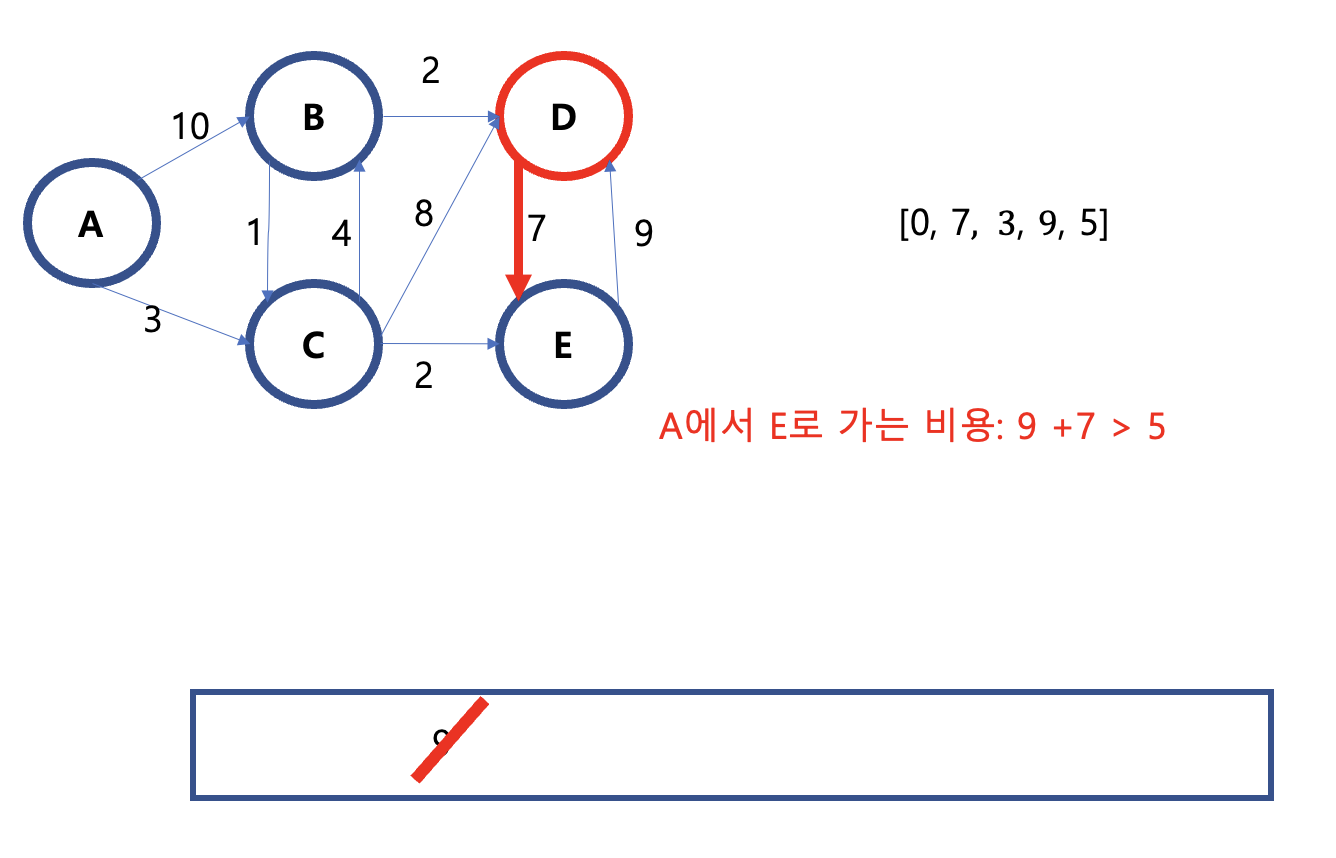
이후 다시 A에서 E로 가는 비용을 조사한 결과, 기존 비용인 5가 더 저렴함으로 교체되지 않고 큐 탐색이 끝난다.
따라서 최종 답안은 [0,7,3,9,5] 가 된다.
3. 풀이
우선순위 큐를 사용하기 위해 최소힙 모듈인 heapq를 사용한다.
import heapq
import sys
graph = {
"A": {"B": 10, "C": 3},
"B": {"C": 1, "D": 2},
"C": {"B": 4, "D": 8, "E": 2},
"D": {"E": 7},
"E": {"D": 9}
}
def dijkstara(start):
distances = {node: sys.maxsize for node in graph}
distances[start] = 0
queue = []
heapq.heappush(queue, (distances[start], start))
while queue:
current_distance, node = heapq.heappop(queue)
if distances[node] < current_distance:
continue
for neighbor_node, distance in graph[node].items():
weighted_distance = current_distance + distance
if weighted_distance < distances[neighbor_node]:
distances[neighbor_node] = weighted_distance
heapq.heappush(queue, (weighted_distance, neighbor_node))
return distances
result = dijkstara("A")
