다익스트라 알고리즘 + 인접행렬을 활용하는 문제였다. 나는 다익스트라 알고리즘의 개념을 완전 까먹고 있었다.
다익스트라 알고리즘 개념은 이 게시글로 포스팅했다.
혹시나 개념을 모른다면 꼭 참고해서 숙지해두길 바란다. heapq 모듈에 대해서도 복습할 수 있다. 다익스트라 풀이법과 모두 동일하다.
1. 문제 설명
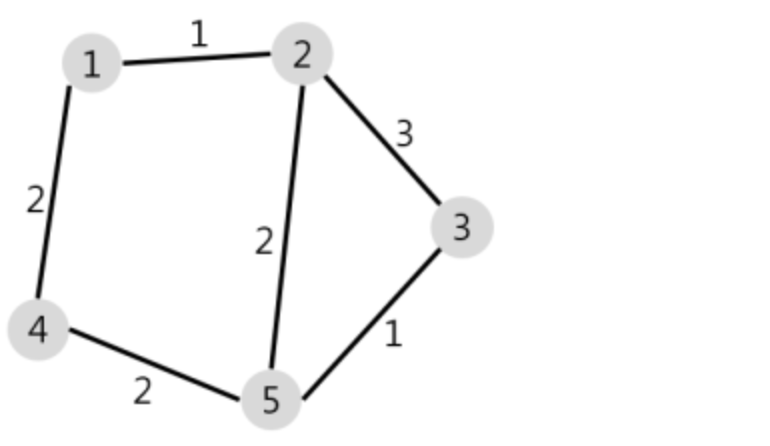
N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
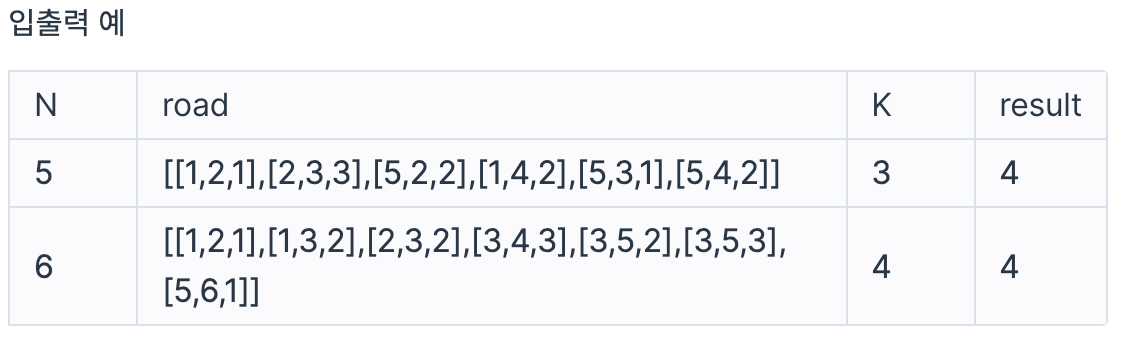
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.
2. 어려웠던점
1) 딕셔너리
딕셔너리 문제를 풀때 항상 꼭 찾아보게 되는 부분이 있다; 기억하자고 했는데 매번 까먹다니.. 나의 뇌..
- 딕셔너리에 해당 키가 존재하는지 확인하기
if not dict.get("key"): -> 없으면 None을 출력한다.
print("Not")
else:
print("Is in!!!")2) 변수명
현재노드의 누적 거리, 바뀐 노드사이의 누적 거리.. 등등 변수명을 짓는데 너무 헷갈렸다...
3) 다익스트라 알고리즘 if 절
다익스트라 알고리즘을 확인하는데에 왜 이 if 문이 필요할까.... 생각했는데 당연하다... 조건을 만족하면 continue로 건너뛰어야 한다.
이미 최소 거리를 만족하기 때문이다.
if distances[node] < current_distance:
continue3. 풀이법
생각보다 복잡하게 풀었다..
노드 간 거리 정보를 딕셔너리 형태로 만드는데 알고리즘이 너무 길어졌다.
이 문제는 몇번 더 복습해서 다익스트라 알고리즘을 머리에 꼭 새겨두자.
import heapq
import sys
def extract_weight(road):
graph = {}
for road_weight in road:
town = str(road_weight[0])
linked_town = str(road_weight[1])
weight = road_weight[2]
if not graph.get(town):
graph[town] = {}
graph[town][linked_town] = weight
else:
if not graph[town].get(linked_town):
graph[town][linked_town] = weight
elif graph[town][linked_town] > weight:
graph[town][linked_town] = weight
if not graph.get(linked_town):
graph[linked_town] = {}
graph[linked_town][town] = weight
else:
if not graph[linked_town].get(town):
graph[linked_town][town] = weight
elif graph[linked_town][town] > weight:
graph[linked_town][town] = weight
return graph
def solution(N, road, K):
graph = extract_weight(road)
distances = {node: sys.maxsize for node in graph}
distances["1"] = 0
queue = []
heapq.heappush(queue, (distances["1"], "1"))
while queue:
current_distance, node = heapq.heappop(queue)
if distances[node] < current_distance:
continue
for neighbor_node, neighbor_distance in graph[node].items():
weight_distance = neighbor_distance + current_distance
if weight_distance < distances[neighbor_node]:
distances[neighbor_node] = weight_distance
heapq.heappush(queue, (weight_distance, neighbor_node))
result = list(filter(lambda x: x[1] <= K, distances.items()))
return len(result)
