[LG aimers 4기] Machine Learning - Bias & Variance

LG aimers 활동을 하며 1달동안 훌륭한 교수진 분들의 강의를 들을 수 있게 되었다.
이전에는 강의를 들으며 실패했던 수업 내용 기록하기 다시 도전 👊
중간중간 관심있는 분야를 우선적으로 들으면서 순서는 뒤죽박죽 될 것으로 예상 !
추가적으로 학교에서 배운 내용도 포함하여 적을 예정이다.

가장 첫 포스팅은 module 3인 machine learning에 대한 전반적인 기초를 훑는 파트이다.

Machine Learning 기초

기본적인 머신러닝 학습 과정은 다음과 같다.
1. data 수집
2. 예측하고자 하는 model class 정의(타겟 설정)
3. model 선정
4. model 학습
5. 성능평가

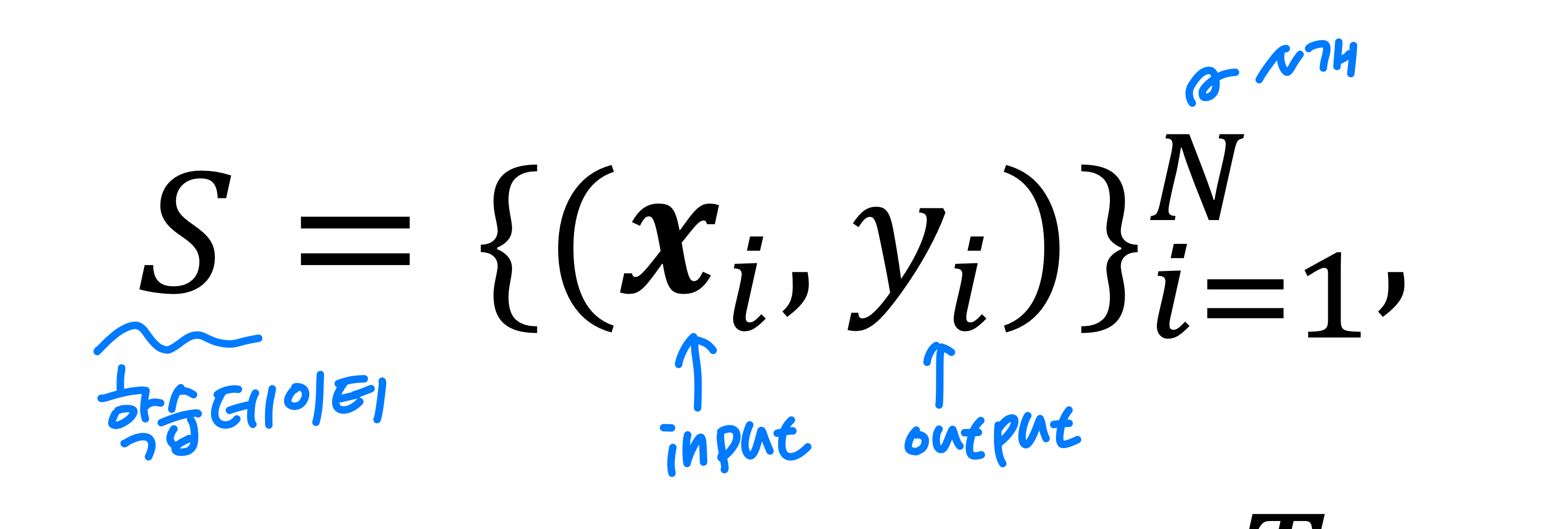
수집된 데이터는 위의 그림과 같이 표현될 수 있다. 학습 데이터 S는 input과 output의 쌍으로 총 N개의 데이터 집합이다. 이때 -1 혹은 1인 class를 linear model을 활용해 학습시키고자 한다면 다음과 같은 w, b의 파라미터가 생성된다.

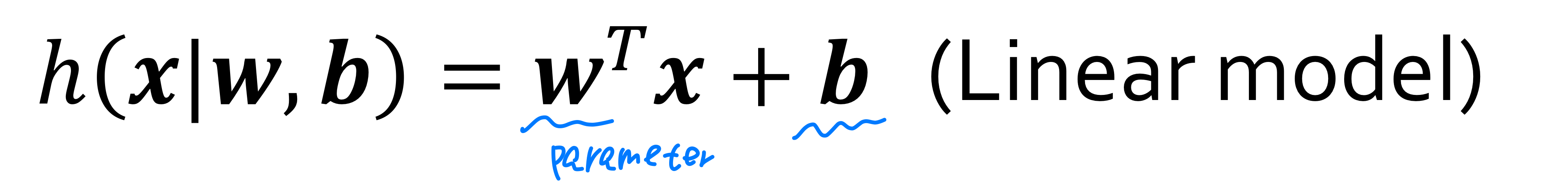
parameter는 모델 학습을 통해 결정되는 일반 parameter와 사용자가 학습 이전에 미리 전달하는 하이퍼파라미터(hyperparameter)가 있다.
위와 같은 선형 모델에서의 파라미터는 모두 일반 parameter에 속한다.

• 하이퍼파라미터(Hyperparameter)
  - ex. RandomForest 모델의 최대 깊이와 같은 parameter를 의미
  • 하이퍼파라미터는 모델에 따라 모수가 다르며 교차검증을 통해 결정한다.
    ex) gridsearch
  • 이때 validation set을 사용해 초모수 튜닝을 진행한다.

결과적으로 기계학습의 목표는 S에 대해서 잘 동작하는 최적의 파라미터 w와 b를 찾아야 한다. 이러한 최적의 파라미터 값을 찾기 위해 일반적으로 손실함수(Loss Function)을 사용한다.

Loss Function: 주어진 Input에 대해서 모델이 예측한 예측값과 정답값을 비교하여 그 차이를 반환하는 함수이다. 좋은 모델을 만들려면 이러한 손실함수를 최소화 시키는 방향으로 학습시켜야 한다.

일반적으로 regression 문제에선 MSE(Mean Squared Error)를 사용하고 classification 문제에선 zero-one loss를 사용한다.

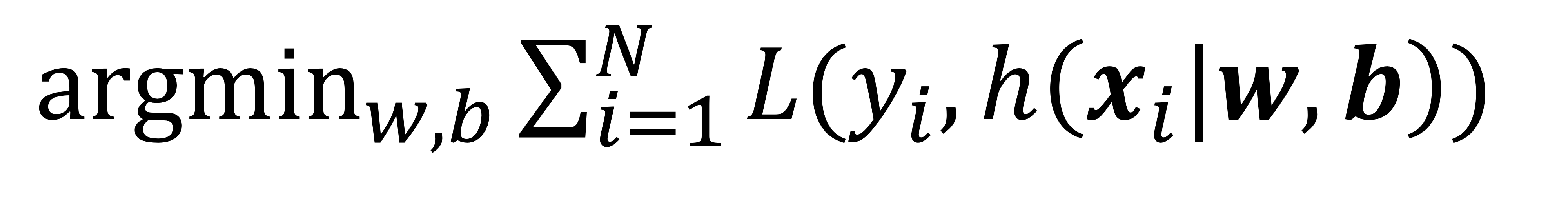
각 데이터가 독립사건으로 얻어졌다고 하면 학습 데이터에 대한 전체 Loss는 각 데이터의 loss값들의 합이 된다. 최종적으로 loss 함수를 최소화하는 w와 b를 찾는 과정이다.

기계학습에 있어 일반화 능력은 매우 중요하다.
기계학습의 일반화란 학습한 데이터에 대해서 잘 되는 것보다 학습 과정 동안에 보지 못한 새로운 데이터에 대해서 잘하는 것이 중요하다.
하지만 학습을 진행하다보면 여러가지 문제에 부딪힌다. 대표적으로 overfitting과 underfitting이다.

Overfitting, Underfitting

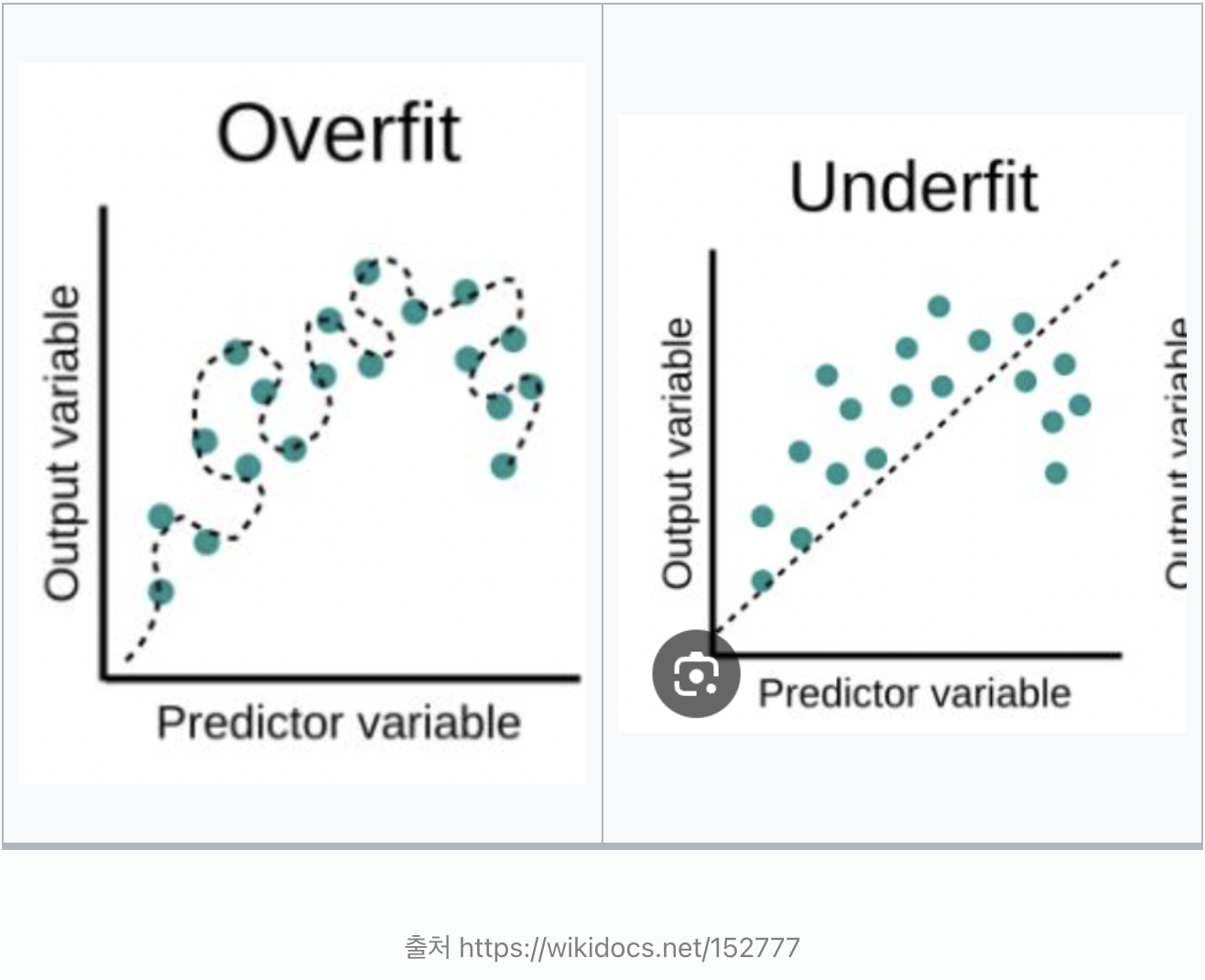
Overfitting은 모델이 train data에 과하게 적합된 것을 의미한다. 즉, train data가 아닌 다른 데이터가 들어오면 잘 못 맞출 가능성이 높다.

underfitting은 모델이 train data조차 잘 맞추지 못하는 경우이다.
이 경우가 overfitting보다 더 안 좋으므로 절대 발생하지 말아야 하는 상황이다. train data조차 잘 학습하지 못한다면 전혀 필요없는 모델이기 때문이다.

따라서 모델을 학습시킬 때 1차 목표는 overfitting 시키는 것이다.
1차적으로 overfitting ➡️ training error < validation error (차이가 매우 클 경우) ➡️ validation error를 낮추는 것을 2차적으로 진행

Typical relation between capacity and error

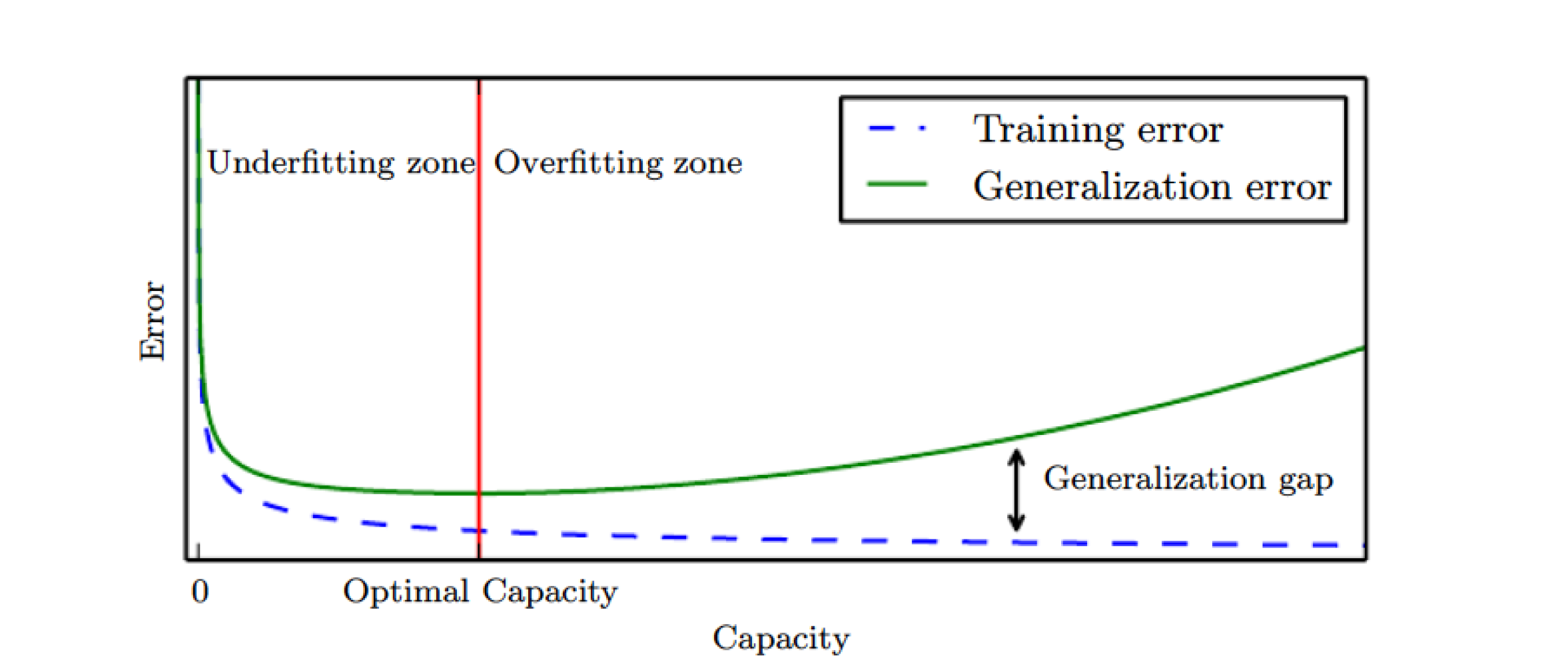
일반적으로 모델의 용량이 커질수록 training error는 무조건 작아진다.하지만 우리가 원하는 최종 목표는 모델의 일반화 성능을 높이는 것이다. 즉, generalizatioin error와 training error를 최소화 시키는 최적의 모델 capacity를 찾아야 한다.

generalization error는 새로운 데이터에 대한 예측값과 정답값의 차이이므로 실제 데이터가 주어지기 전까진 알 수 없다. 따라서 validation set을 활용한 validation error로 generalization error를 예측할 수 있다.

Regularization

overfitting을 방지하기 위한 방법으로 Regularization이 있다.
예를 들어 선형 회귀에 대한 목적 함수가 다음과 같을 때 error(loss function)만을 사용한 학습은 과적합에 빠질 수 있으므로 Regularization Term을 추가한다.

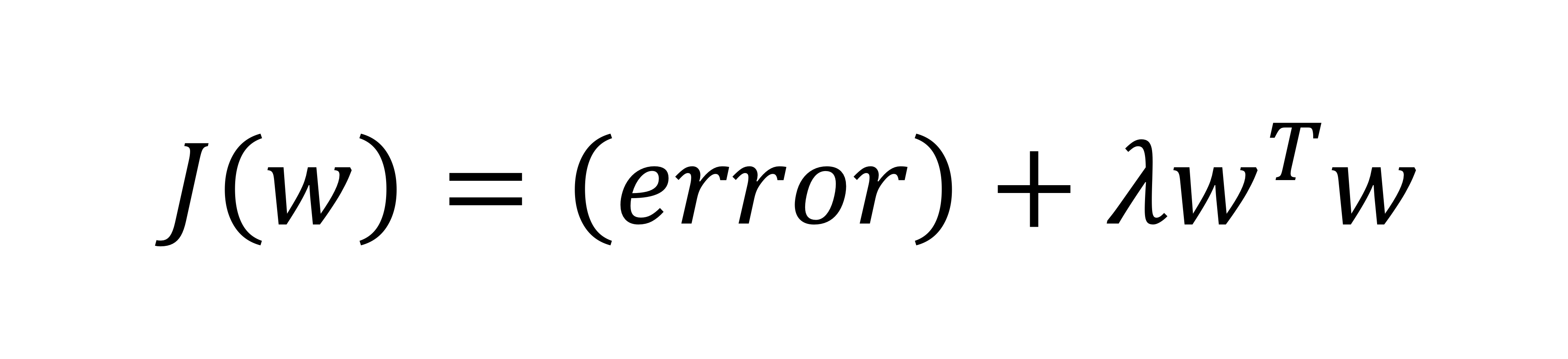
$\lambda$는 목적함수가 두 가지 component로 구성되어 있기에 상대적인 중요성을 준다.
$\lambda$를 작게 주면 첫번째 텀만 고려(error), $\lambda$를 크게 주면 두번째 텀을 더 고려한다.

regularization의 목적은 generalization error를 낮추는 것이지 training error를 낮추는 것은 X

training error을 낮추고 싶으면 error만을 사용해 학습하는게 더 효과적

Bias/Variance (편향/분산)

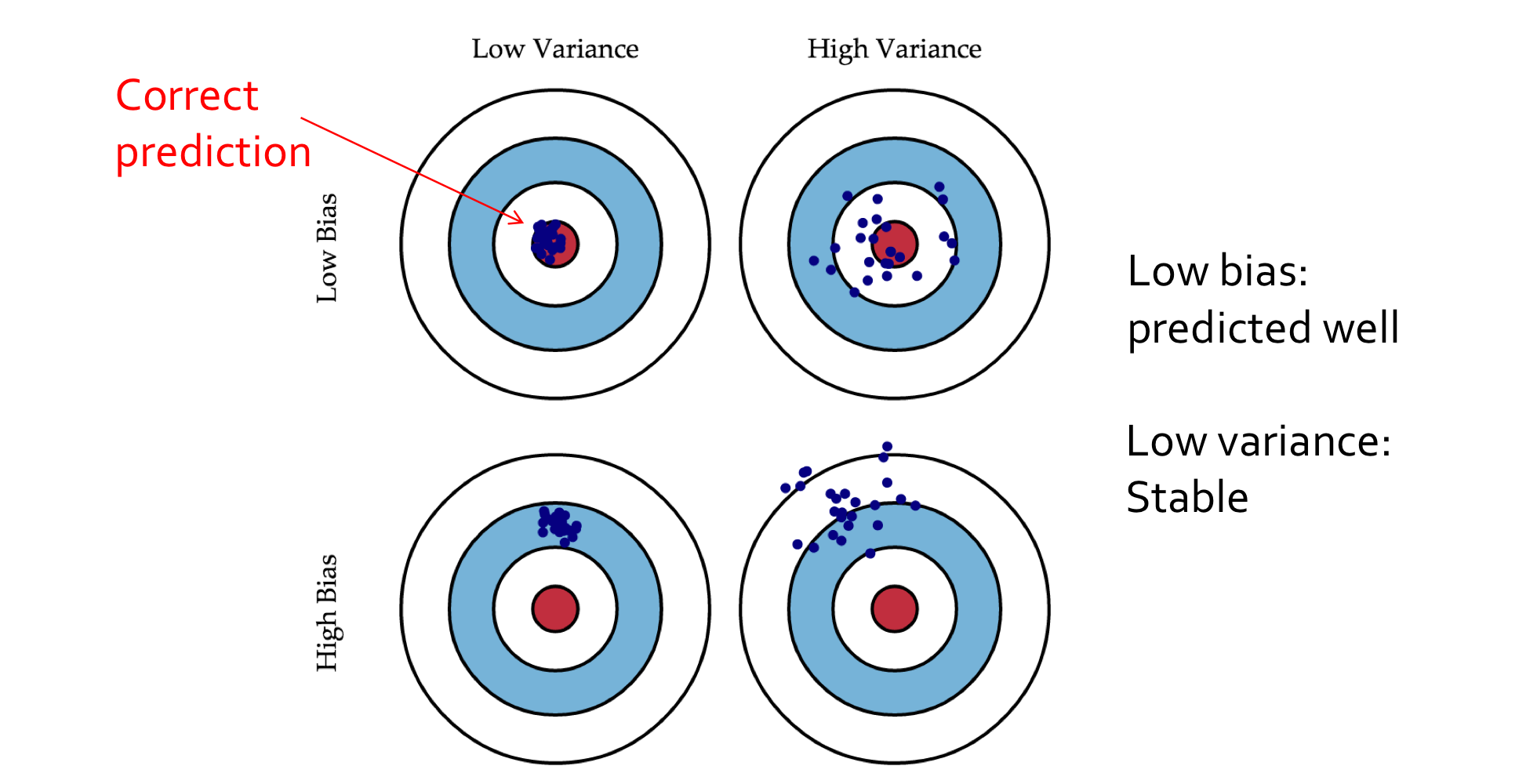
• Bias
  bias(편향)은 예측값과 정답값 간 차이의 평균이다.
  
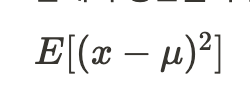
  즉, 모델이 얼마나 잘 맞추는지를 표현한다. 정답을 과녁의 중심이라고 한다면 그 예측값들이 정답과 얼마나 떨어져 있는가이다.
  • bias가 낮을수록 과녁의 중심 근처에 예측값들이 존재한다.

• Variance
  variance(분산)은 예측값들이 퍼져있는 정도를 의미한다. 이건 모델이 얼마나 안정적으로 맞추는지를 표현한다.
  
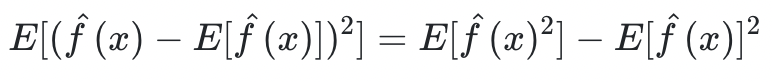
  ➡️ 예측값과 예측값들의 평균의 각 거리를 제곱한 값들의 최종 평균
  

이러한 bias(편향)과 variance(분산)은 서로 Trade-off 관계를 가진다.
test error = bias + variance로 구성되어 있다.
일반화 능력을 높이기 위해선 bias와 variance 모두 낮춰야 하지만 하나가 낮으면 하나가 높기 때문에 실현하긴 어렵다. 이를 해결하기 위해 앙상블 learning이 활용된다.

• 모델의 capacity(복잡도) ⬆️ Bias ⬇️ Variance ⬆️
  • 복잡도가 클수록 training error 낮아짐 -> overfitting
  • 특정 데이터셋에 과적합 되었기에 새로운 데이터가 들어오면 안정적으로 예측하지 못하고 들쑥날쑥 예측
  • 높은 Variance를 잡기 위해선 최대한 많은 데이터를 모으는 것
  • regularization은 데이터가 부족할 때 preference를 주기 위해 사용한 것이고 가장 좋은건 데이터를 많이 모아 overfitting을 더 시키는 것이다.
• 모델의 capacity(복잡도) ⬇️ Bias ⬆️ Variance ⬇️
  • 복잡도가 낮을수록 underfitting
  • 잘 맞추지 못하니 편향은 높음
  • 하지만 모든 데이터셋에 대해서 전반적으로 잘 못 맞출 것이기에 퍼져있는 정도는 낮음
  • 높은 Bias는 데이터를 많이 모아도 해결할 수 없음. 애초에 모델 복잡도가 낮을 때 발생하기에 어떤 양의 데이터를 가져와도 결국 선형밖에 못 그린다면 쓸모없는 모델이 됨.