이번 게시물에서는 연쇄 행렬곱셈에 대해 부르트 폴스 알고리즘과 다이나믹 프로그래밍을 이용한 알고리즘을 알아보겠다.
iXj행렬과 jXk행렬을 곱하기 위해서는 iXjXk번의 기본 곱셈이 필요하다. 이러한 상황에서 연쇄적으로 행렬을 곱할 때, 곱하는 순서에 따라 기본 곱셈의 횟수가 달라지게 된다. 이러한 상황에서, 어떤 순서로 곱해야 기본 곱셈의 횟수가 가장 적어지는 지 구하는 것이 이번 알고리즘의 목표이다. 따라서 최적화 문제라고 볼 수 있다.

위의 사진은 교재에서 제공된 사진인데, 이처럼 모든 경우의 수를 다 구한 후, 이들끼리 비교하는 것을 부르트 폴스 알고리즘이라 볼 수 있겠다.
위처럼 부르트 폴스 알고리즘으로 문제를 해결한다 가정했을 때의 시간 복잡도는 최소한으로 잡아도 exponential이 되어버린다.
증명
T(n): n 개의 행렬을 곱할 수 있는 모든 순서의 가짓수
첫 번째 행렬을 가장 마지막에 곱한다고 가정했을 때의 모든 곱할 수 있는 순서의 가짓수는 T(n-1)이다. 이렇게 되면, T(n) = n x T(n-1) 이라 할 수 있고, 현재 시간복잡도가 최소일 경우를 구하고 있으므로 n을 2로 잡으면,
T(n) >= 2T(n-1) 이고, 우리는 T(2) = 1 이라는 사실을 이미 알고있다.
따라서 T(n) >= 2T(n-1) >= 2^2T(n-2) ...>=2^(n-2)T(2) = 2^(n-1) 이고, 해당 알고리즘의 시간 복잡도는 최소한 2^n 이라고 할 수 있다.
이렇게 부르트 폴스 알고리즘으로 해결할 시, 시간 복잡도가 exponantial인 것을 확인했다. 그렇다면 어떻게 해야 시간 복잡도를 줄이면서 곱셈 횟수가 최소인 연쇄 행렬 곱셈 순서를 찾아낼 수 있을까?
일단 모든 경우의 수를 파악하는 것은 힘들다는 사실을 우리는 알고 있다. 그렇다면 하위 문제를 먼저 푼 상태로 상위 문제에 접근하는 다이나믹 프로그래밍을 사용해보면 어떨까.
iXj행렬과 jXk행렬을 곱하기 위해서 ixjxk번의 일반 곱셈이 필요하고, 이 둘을 곱하면 ixk행렬이 됨을 주목하자.
이는 반대로 생각하면, ixk행렬까지를 만드는 데 필요한 곱셈의 수가, ixj행렬과 jxk행렬을 만드는 데 필요했던 곱셈의 수를 더하고, 여기에 이 두 행렬을 서로 곱하는 데 발생하는 ixjxk번에 곱셈 횟수를 더한 수가 된다고 할 수 있다.
이렇게 생각하면, 문제를 가장 말단까지 쪼갠 후, 하위 문제에서부터 시작하는 것이 가능해진다.
일반화시키면, d(k)를 행렬 A(k)의 열이라고 하고, 그에 따라 d(k-1)를 행렬 A(k)의 행이라고 했을 떄,
1<=i<=j<=n 일 때
M[i][j] = i<j 일 때 A(i)부터 A(j)까지의 행렬을 곱하는 데 필요한 최소 곱셈 횟수
=(i<=k<=j-1일 때)minimum(M[i][k]+M[k+1][j]+d(i-1)d(k)d(j));
M[i][i] = 0;
로 표현할 수 있다.
이를 설명하기 위해 교재에서 사용한 예제는 이것이다.
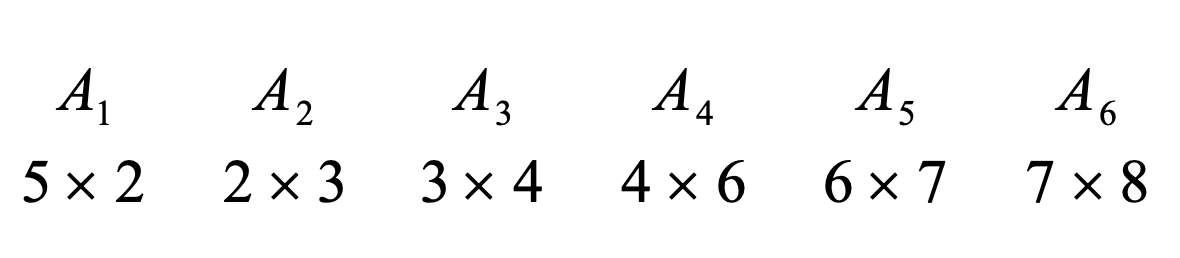
위에서 제시한 식을 활용하여 M[3][5]를 구해보겠다.
M[3][5] = minimum(M[3][k]+M[k+1][5]+d(2)d(k)d(5)) //3<=k<=4
=minimum(M[3][3]+M[4][5]+3x4x7, M[3][4]+M[5][5]+3x6x7)
=minimum(0+4x6x7+3x4x7, 3x4x6+0+3x6x7)
=minimum(252, 198)
=198
이렇게 모두 계산했을 때의 배열이다.

가장 왼쪽에서 시작하는 대각선일수록 하위 문제이므로, 최종 결과값은 가장 마지막 대각선에 위치한 M[1][6]이 됨을 알 수 있다.
이러한 알고리즘을 바탕으로 하여 슈더코드를 작성해 보겠다.
int minmult(int n, const int d[], int P[][]){
int i,j,k,diagonal;
int M[1..n][1..n];
for(i=1;i<=n;i++)
M[i][i] = 0;
for(diagonal = 1; diagonal <= n-1; diagonal++){
for(i=1; i<=n-diagonal; i++){
j = i+diagonal;
M[i][j] = minimum(M[i][k]+M[k+1][j]+d[i-1]*d[k]*d[j]); //i<=k<j 일 때
P[i][j] = k //that gives minimum
}
}
return M[1][n];
}이제, 방금 알아본 연쇄 행렬곱셈 알고리즘에 대하여 복잡도 분석을 진행해 보겠다.
단위연산: 각 k값에 대하여 실행된 명령문(최소값인 지를 알아보는 비교문 포함)
입력크기: 곱할 행렬의 수(n)
<분석>
i루프를 수행하는 횟수: n-diagonal
k루프를 수행하는 횟수: k가 i일 때 부터 j-1일 때 까지 수행하므로 (j-1)-i+1 이고, 이때 j=i+diagonal이므로, ((i+diagonal)-1)-i+1=diagonal
따라서, diagonal이 1일때부터 n-1일때까지 (n-diagoanl)xdiagonal을 해주면 제곱을 모두 더하는 꼴이 되므로 n(n-1)(n+1)/6 즉, 시간복잡도는 n^3이 된다.
이를 통하여, 다이나믹 프로그래밍을 사용하는 것이 브루트 폴스보다 성능이 좋다는 것을 알 수 있다.
