MST와 Prim's Algorithm

MST(Minimum Spanning Tree)에 대해 알아보기 전에, Spanning Tree가 무엇인지부터 차근차근 알아보자.

Spanning Tree(신장 트리)란, 연결된 비방향성 그래프에서 Cycle(순환 경로)를 만드는 요소들을 제거하여 트리가 된 그래프를 의미한다. 이 Cycle을 만드는 요소를 제거하는 과정에서, Spanning Tree의 비용이 최소가 되도록 제거하면, 그것을 최소 비용 신장 트리 즉, MST라고 한다.

MST를 만드는 알고리즘은 다양하게 존재하지만, 이번에는 Prim 알고리즘을 이용하여 MST를 만들어 보겠다.

Prim 알고리즘의 아이디어를 코드로 표현해보면 이러하다.

F = ø;        //비어 있는 edge들의 집합 F 생성
Y = {v1};	  //이미 연결된 정점들을 넣을 집합 초기화

while (the instance is not solved){
	select a vertex in V-Y that i nearest to Y;
    //아직 선택되지 않은 정점 중 이미 선택된 정점들과 가장 가까운 정점 선택
    add the vertex to Y;  //선택된 정점을 집합 Y에 추가
    add the edge to F;    //선택된 간선을 집합 F에 추가
    
    if(Y==V)			  //Y에 모든 정점이 포함되면 문제 해결
   		the instance is solved;
}

해당 코드를 분석하여 Prim 알고리즘의 작동 방식을 살펴보자.
알고리즘에 총 4개의 집합이 존재한다. 선택된 간선을 담을 집합 F, 모든 정점의 집합 V, 선택된 정점들의 집합 Y, 선택되지 않은 정점들의 집합 V-Y이다.

1. Y에 초기값인 v1을 넣는다.
2. 집합 Y에 들어있는 정점과 가장 가까운 정점을 선택한다.
3. 해당 정점을 집합 Y에, Y의 정점과 해당 정점을 잇는 간선을 집합 F에 넣는다.
4. 집합 Y에 모든 정점이 포함될때까지 2,3 을 반복한다.

위의 작동 방식을 구체화시켜보자.
구체화를 위해 데이터를 도입시켰다.

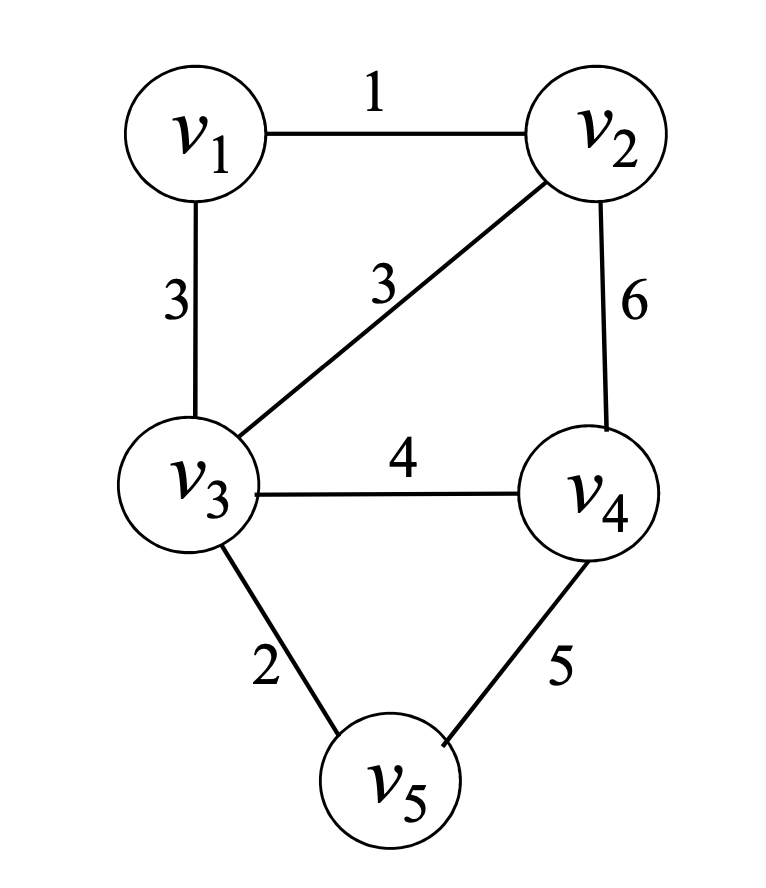
이 그래프를 인접행렬식으로 표현하면

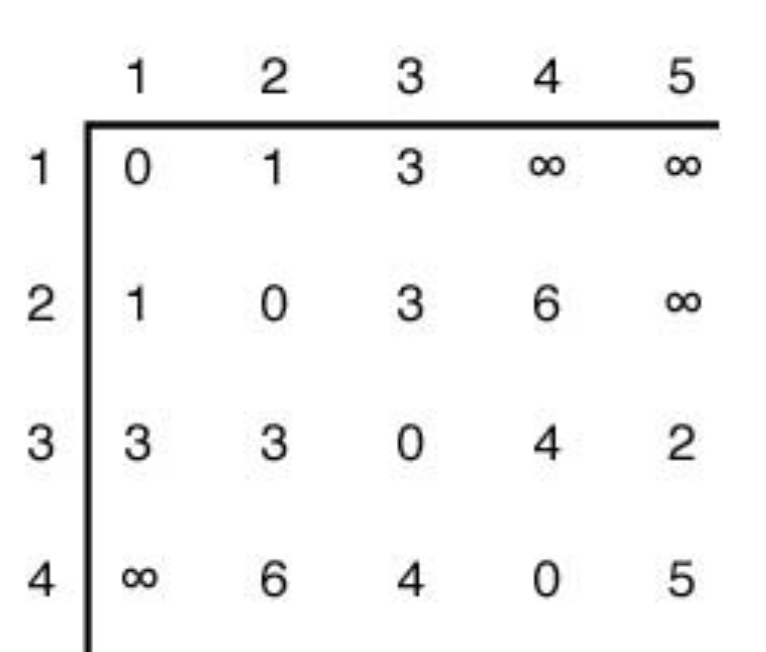
이렇게 나타낼 수 있다.
해당 배열을 W[i][j]라고 하고, nearest[], distance[]배열을 도입한다.
-nearest[i]=Y에 속한 정점 중 vi에 가장 가까운 정점의 인덱스
-distance[i]=vi과 nearest[i]를 잇는 간선의 가중치
-vnear=i
[psuedo code]

void prim(int n, const number W[][], set_of_edges& F){
	index i, vnear; number min; edge e;
    index nearest[2..n];
    number distance[2..n];
    
    F=ø;
    for(i = 2; i<=n ; i++){
    	nearest[i]=1;
        distance[i]=W[1][i];
    }
    repeat(n-1 times){
    	min = "infinite";
        for(i=2;i<=n;i++){
        	if(0<=distance[i]<=min){
            	min = distace[i];
                vnear = i;
            }
        }
        e = edge(vnear, nearest[vnear]);
        add e to F;
        distance[vnear] = -1;
        for(i=2;i<=n;i++){
        	if(W[i][vnear]<distance[i]){
            	distance[i]=W[i][vnear];
                nearest[i] = vnear;
            }
        }
    }
}