Query Optimization (2)

Statistical Information for Cost Estimation

• $n_r$: relation r의 튜플 수

• $b_r$: r의 튜플을 포함하는 블록 수

• $l_r$: r의 튜플의 사이즈

• $f_r$: r의 차단 인자 - 즉, 하나의 블록에 맞는 r의 튜플의 개수이다.

• V(A, r): r에 나타나는 속성 A의 개별 값의 수; $π_A(r)$ 의 크기와 같다.

• r의 튜플이 파일에 물리적으로 함께 저장되어 있으면,

  

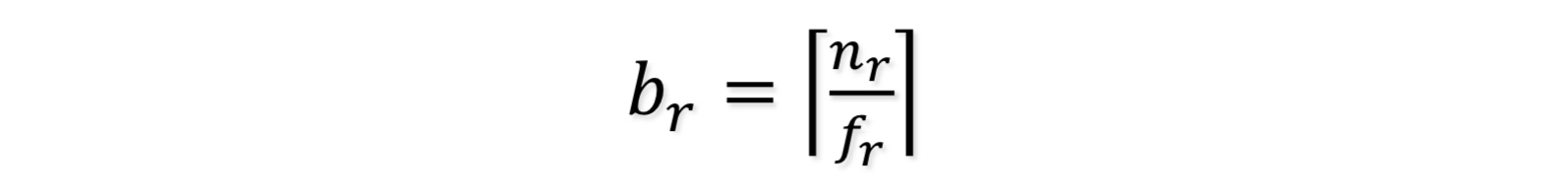
Histograms

• 실제 optimizer는 종종 정확도를 향상시키기 위해 통계 정보를 유지한다.

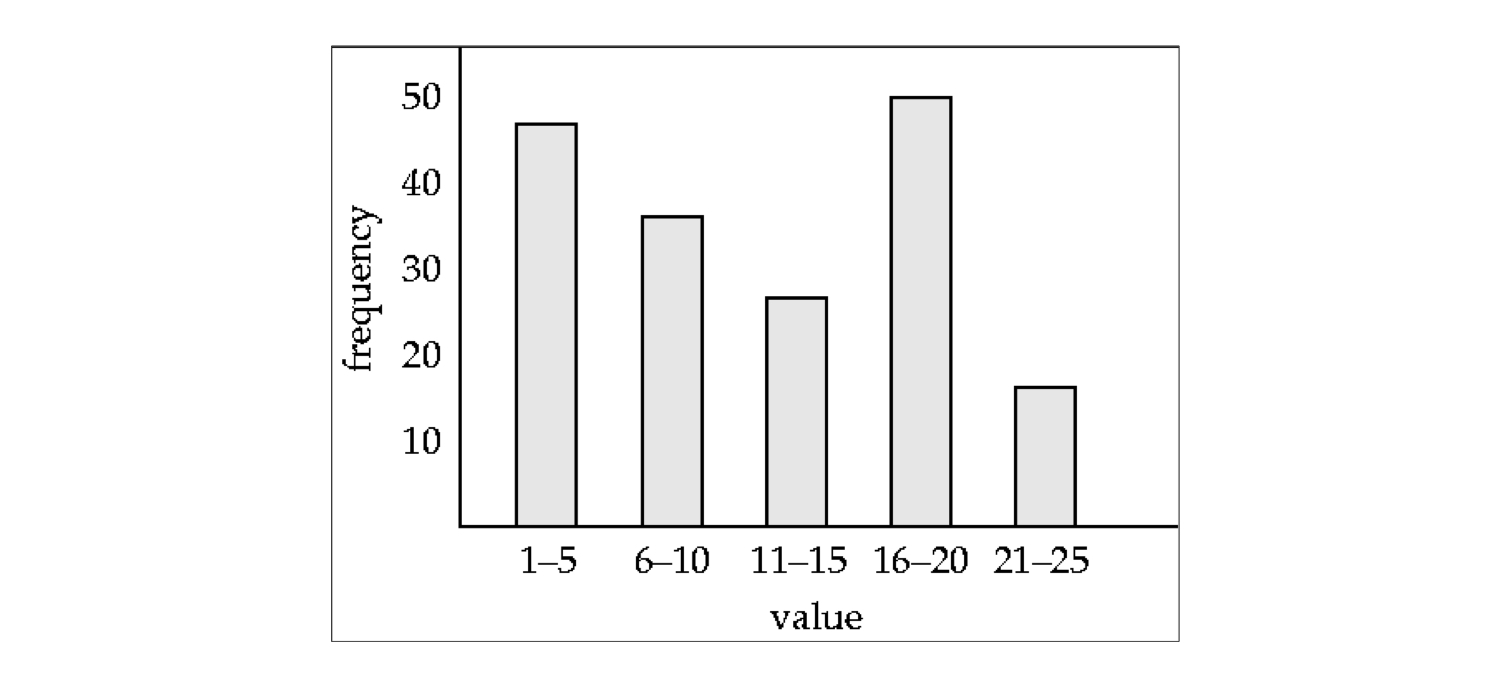
  e.g.) 각 속성 값의 분포를 히스토그램으로 저장
  

• relation person의 age 속성에 대한 히스토그램

Selection Size Estimation

• $σ_{A=v}(r)$

  • $n_r/V(A,r)$: selection을 만족시키는 레코드 수

    • 근사치로 사용되는 균일 분포

  • 키 속성에 대한 동등 조건: 예상 크기 = 1

• $σ_{A<=v}(r)$ ($σ_{A>=v}(r)$의 경우도 대칭적)

  • c는 조건을 만족하는 예상 튜플 수를 나타낸다.

  • min(A, r) 및 max(A, r)가 카탈로그에서 사용한 경우이다.

    • c = 0 if v < min(A, r) ⇒ 스페셜 케이스

    • c = $n_r$(v-min(A, r)) / max(A, r) - min(A, r) ⇒ 일반적인 케이스

  • 히스토그램을 사용할 수 있는 경우 위의 추정치를 세분화할 수 있다.

  • 통계 정보가 없는 경우 c는 $n_r/2$ 로 가정한다. (=퉁친다.)

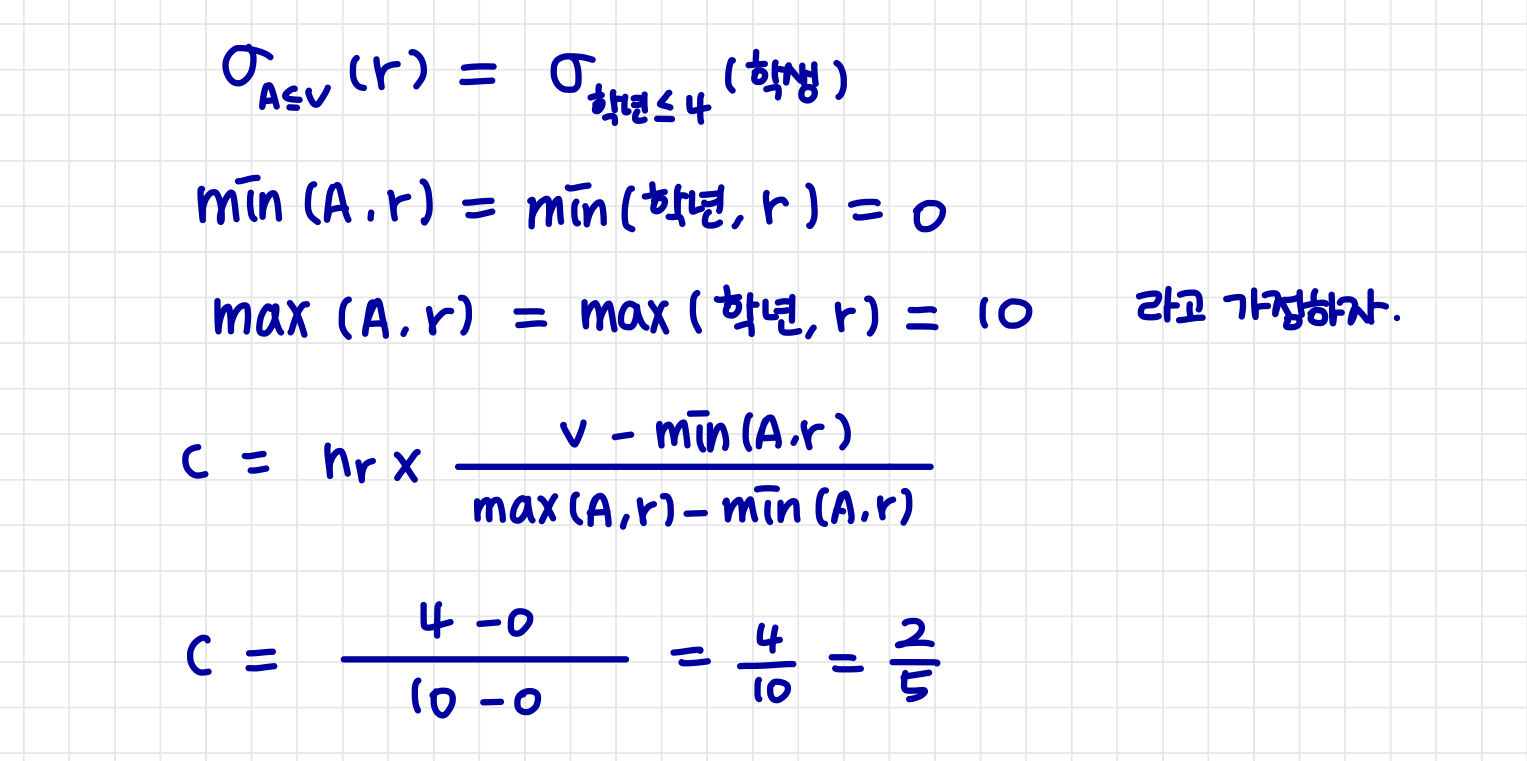
Size Estimation of Complex Selections

• 조건 $θ_i$ 의 선택도는 relation r 의 튜플이 $θ_i$ 를 만족할 확률이다.

  • $s_i$ 가 만약 r에서 만족하는 튜플의 수인 경우, $θ_i$ 의 선택도는 $s_i/n_r$ 으로 지정된다.

• 논리 곱 (conjunction, ∧): $*σ_{θ_1∧θ_2∧...∧θ_n}(r)$.* 독립성을 가정하면 결과의 튜플 추정치는 다음과 같다.

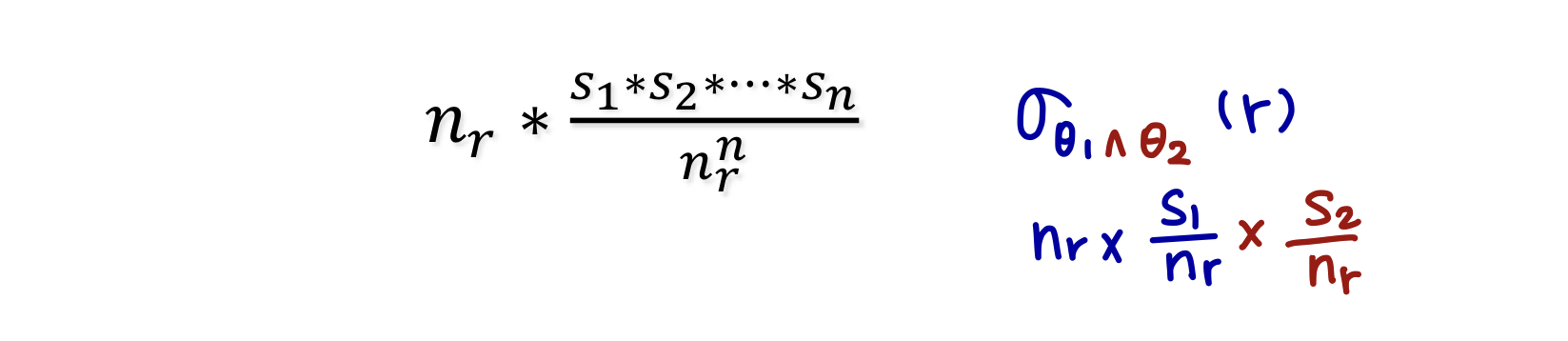
Size Estimation of Complex Selections (Cont.)

• 논리 합 (disjunction, ∨): $*σ_{θ_1∨θ_2∨...∨θ_n}(r)$.* 추정 튜플 수는 다음과 같다.

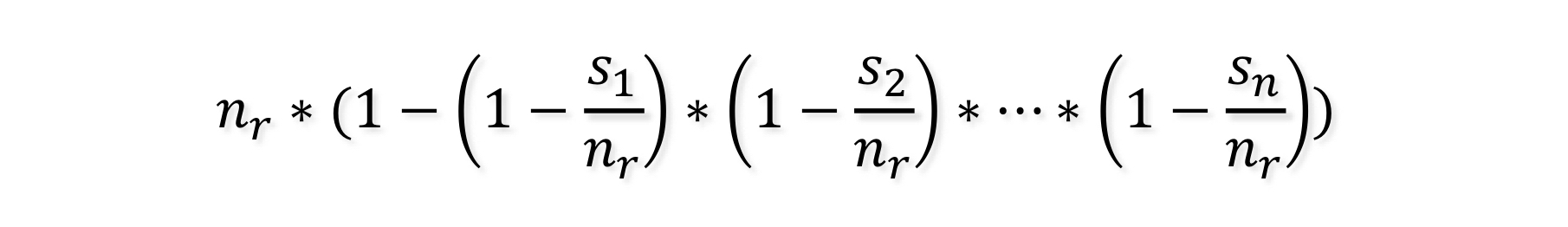
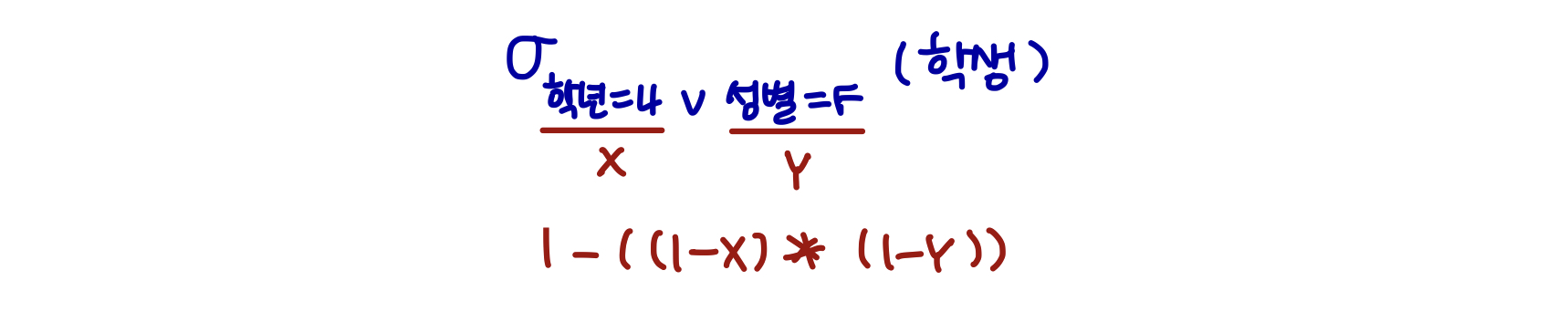
• 부정 (negation): $σ_{¬θ}(r)$. 추정 튜플 수는 다음과 같다.

  $n_r - size($$σ_θ(r))$
  

Join Operation: Running Example

실행 예시: depositor ⋈ customer

join 예제에 대한 카탈로그 정보:

• $n_{customer}$ = 10,000.

• $f_{customer}$ = 25, 이는 $b_{customer}$ = 10000/25 = 400. 을 암시한다.

• $n_{depositor}$ = 5000.

• $f_{depositor}$ = 50, 이는 $b_{depositor}$ = 5000/50 = 100. 을 암시한다.

• V(customer-name, depositor) = 2500, 이는 평균적으로 각 고객이 두 개의 계좌를 가지고 있음을 의미한다.

  • 또한 depositor의 customer-name은 customer의 foreign key라고 가정한다.

• V(customer-name, customer) = 10,000 (primary key!)

Estimation of the Size of Joins

• 데카르트 곱 r x s는 $n_r . n_s$ 튜플을 포함한다; 각 튜플은 $l_r+l_s$ bytes를 차지한다.

• 만약 R ∩ S = ∅ 이면, r ⋈ s는 r x s 와 동일하다.

• 만약 R ∩ S 가 R의 key 라면, s의 튜플은 r에서 최대 하나의 튜플과 결합한다.

  • 그러므로, r ⋈ s 의 튜플 수는 s 의 튜플 수보다 크지 않다.

Estimation of the Size of Joins (Cont.)

• S의 R ∩ S가 S가 R을 참조하는 S의 외래키인 경우, r ⋈ s 의 튜플 수는 S의 튜플 수와 정확히 동일하다.

  • R ∩ S가 S를 참조하는 외래 키인 경우는 대칭이다.

• depositor ⋈ customer 의 예시 쿼리에서, depositor에 있는 customer-name은 customer의 외래키이다.

  • 따라서, 결과는 정확히 $n_{depositor}$ 튜플을 가진다. (which is 5000)

Estimation of the Size of Joins (Cont.)

• 만약 R ∩ S = {A} 이 R 이나 S 의 키가 아니고 R의 모든 튜플 t가 R ⋈ S의 튜플을 생성한다고 가정하면 R ⋈ S의 튜플 수는 다음과 같이 추정된다.
  

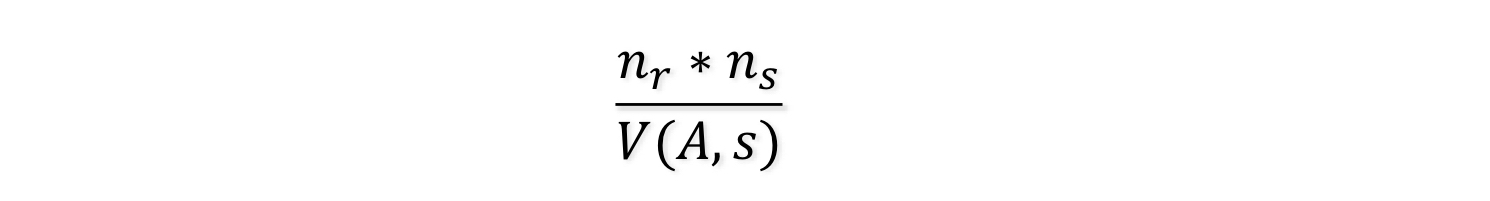
만약 반대경우가 true라면, 다음과 같이 추정된다: (S의 모든 튜플 t가 R ⋈ S의 튜플을 생성한다고 가정)

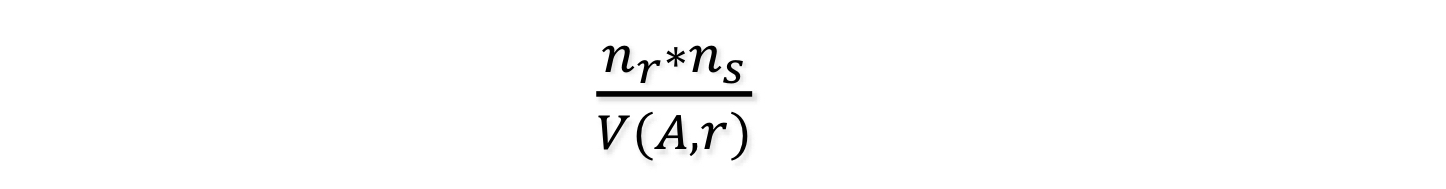
• 히스토그램을 사용할 수 있는 경우 위에서 개선할수 있다.

  • 두 relation에 관한 히스토그램의 각 셀에 대해 위와 유사한 공식을 이용한다.

Estimation of the Size of Joins (Cont.)

• 외래키에 대한 정보를 사용하지 않고 depositor ⋈ customer 에 대한 크기 추정치를 계산한다.

  • V(customer-name, depositor) = 2500 and V(customer-name, customer) = 10000

  • 두 추정치는 500010000/2500 = 20,000 and 500010000/10000 = 5000

  • 더 낮은 추정치(5000)를 선택하는데, 이 경우 외래키를 사용한 이전 계산과 동일하다.

Size Estimation for Other Operations

• aggregation 추정 크기와 위와 같은 이유는 A의 각 고유 값에 대해 aGf(r)에 하나의 튜플이 있기 때문이다.

• 집합 연산

  • 동일한 relation에서 선택 항목의 합집합 / 교집합: 선택 항목에 대한 크기 추정치를 다시 작성하고 사용한다.

    • $σ_{θ1}(r)∪σ_{θ2}(r)$ 은 $σ_{θ1∨θ2}(r)$ 로 다시 쓸 수 있다.

  • 다른 relation에 대한 작업

    • r ∪ s 추정 크기 = r 의 크기 + s 의 크기

    • r ∩ s 추정 크기 = r 의 최소 크기와 s 의 크기

    • r - s 의 추정 크기 = r

    • 세 가지 추정치 모두 상당히 부정확할 수 있지만 크기에 대한 상한선을 제공한다.

Size Estimation (Cont.)

• Outer join:
  

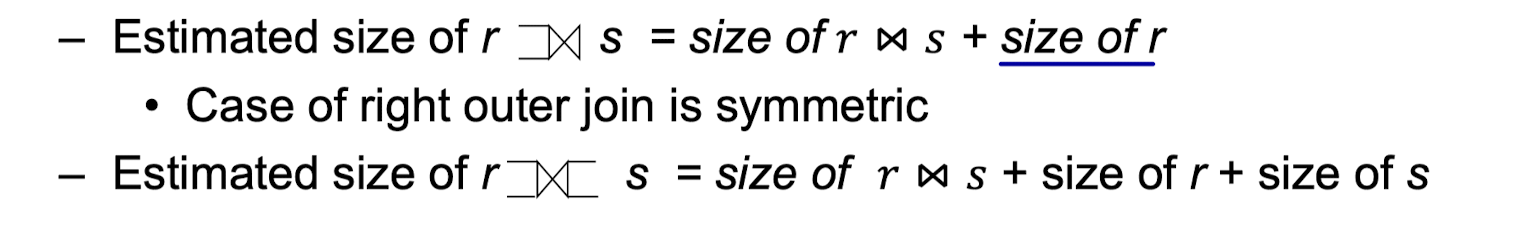
Estimation of Number of Distinct Values

Selections: $σ_θ(r)$

• θ 가 A가 지정된 값을 취하도록 강제하는 경우: V(A, $σ_{θ}(r)$) = 1.

  • e.g., A = 3, year = 2016

• θ 가 A가 지정된 값 세트 중 하나를 취하도록 강제하는 경우:

  • V(A, $σ_{θ}(r)$) = 지정된 값의 수

  • e.g., A = 1 ∨ A = 3 ∨ A = 4

• 선택 조건 θ가 A op r 식인 경우: V(A, $σ_{θ}(r)$) = V(A, r) * s

  • 여기서 s는 선택의 선택도이다.

• 다른 모든 경우: 대략적인 추정치를 사용한다.: min(V(A, r), $n_{σ_{θ}(r)}$)

  • 더 정확한 추정치는 확률 이론을 사용하여 얻을 수 있지만 이는 일반적으로 잘 작동한다.

Estimation of Distinct Values (Cont.)

Joins: r ⋈ s

• A의 모든 속성이 r에서 온 경우

  • 추정 V(A, r ⋈ s) = min (V(A, r), $n_{r⋈s}$)

• A가 r의 속성 A1과 s의 속성 A2를 포함하는 경우

  • 추정 V(A, r ⋈ s) = min( V(A1, r) V(A2 - A1, s), V(A2, s) V(A1 - A2, r), $n_{r⋈s}$)

  • 더 정확한 추정치는 확률 이론을 사용하여 얻을 수 있지만 이는 일반적으로 잘 작동한다.

Materialized Views

• 구체화된 뷰는 내용이 계산되고 저장되는 뷰이다.

• consider the view (materialized view)

• 위의 view를 materialized하는 것은 총 대출 금액이 자주 필요한 경우에 유용할 것이다.

  • 여러 튜플을 찾고 그 양을 합산하는 수고를 덜 수 있다.

Materialized View Maintenance

• 기본 데이터로 구체화된 뷰 (materialized view)를 최신 상태로 유지하는 작업을 구체화된 뷰 유지 관리(materialized view maintenance)라고 한다.

• 구체화된 뷰는 업데이트할 때마다 재계산하여 유지 관리할 수 있다.

• 더 나은 옵션은 증분 보기 유지 관리(incremental view maintenance)를 사용하는 것이다.

  • 데이터베이스 relation에 대한 변경 사항은 구체화된 뷰에 대한 변경 사항을 계산하는 데 사용되며 이후 업데이트 된다.

• 뷰 유지보수는 다음과 같이 수행할 수 있다.

  • view 정의에서 각 relation의 삽입, 삭제 및 업데이트에 대한 트리거를 수동으로 정의한다.

  • 데이터베이스 relation이 업데이트될 때마다 view를 업데이트하도록 수동으로 작성한다.

  • 주기적인 재계산 (e.g., nightly)

  • 위의 방법은 많은 데이터베이스 시스템에서 직접 지원된다.

    • 수작업 / 정확성 문제 방지

Incremental View Maintenance

• relation 또는 식에 대한 변경 (삽입 및 삭제)을 differential(차등)이라고 한다.

  • r에 삽입되고 r에서 삭제된 튜플 집합은 $i_r$ 및 $d_r$ 로 표시된다.

• 설명을 단순화 하기 위해 삽입 및 삭제만 고려한다.

  • 업데이트 튜플을 삽입한 후 튜플을 삭제하여 튜플에 대한 업데이트를 대체한다.

• 입력(input)에 대한 변경 사항이 있을 때 각 relation 연산의 결과에 대한 변경 사항을 계산하는 방법을 설명한다.

• 그런 다음 relational algebra 식을 처리하는 방법을 설명한다.

Join Operation

• 구체화된 뷰 v = r ⋈ s 및 r에 대한 업데이트를 고려한다.

• $r_{old}$ 및 $r_{new}$ 은 relation r의 이전 및 새 상태를 나타낸다.

• r에 대한 삽입의 경우를 고려해보자.

  • $r_{new}$ ⋈ s 를 ($r_{old}$ ∪ $i_r$) ⋈ s 로 쓸 수 있다.

  • 그리고 위의 식은 ($r_{old}$ ⋈ s) ∪ ($i_r$⋈ s) 로 다시 쓸 수 있다.

  • 그러나 ($r_{old}$ ⋈ s)는 단순히 구체화된 뷰의 이전 값이므로 뷰에 대한 증분 변경(incremental change)는 단지 i ⋈ s 이다.

• 그러므로 insert는 $v_{new} = v_{old} ∪ (i_r ⋈ s)$

• delete는 $v_{new} = v_{old} - (d_r ⋈ s)$

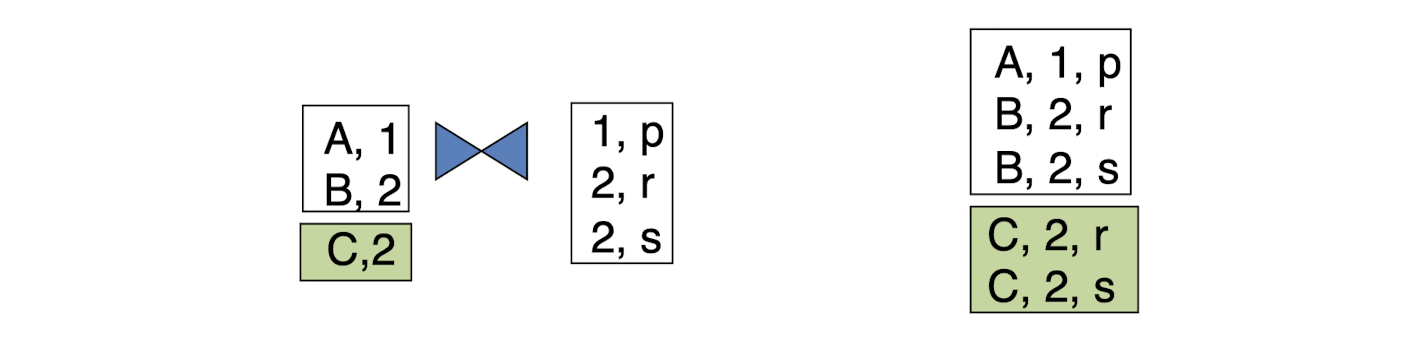
Selection and Projection Operations

• Selection: consider a view v = $σ_{θ}(r)$.

  • $v_{new} = v_{old} ∪ σ_{θ}(i_r)$

  • $v_{new} = v_{old} - σ_{θ}(d_r)$

• Projection은 훨씬 어려운 연산이다.

  • R = (A, B), r = {(a,2), (a,3)}

  • $π_A(r)$ 은 단일 튜플 (a)를 가진다.

  • 만약 r에서 튜플 (a,2)를 삭제하면 $π_A(r)$ 로부터 튜플 (a)가 삭제되면 안된다. 하지만 (a, 3) 까지 삭제하면, 튜플 (a)가 삭제되도 된다.

• $π_A(r)$ 프로젝션의 각 튜플에 대해 파생된 횟수를 카운트한다.

  • r에 튜플을 삽입할 때, 결과 튜플이 이미 $π_A(r)$ 에 있는 경우 카운트를 증분하고, 그렇지 않으면 count = 1인 새 튜플을 추가한다.

  • r에서 튜플을 삭제할 때, $π_A(r)$ 에서 해당 튜플의 개수를 줄인다.

    • 만약 카운트가 0이 되면 $π_A(r)$ 로부터 튜플을 삭제한다.

Aggregation Operations

• 튜플 집합 $i_r$이 삽입될 때

  • $i_r$ 의 각 튜플 r에 대해 해당 그룹이 이미 v에 있으면 카운트를 증가시키고, 그렇지 않으면 카운트 =1인 새 튜플을 추가한다.

• 튜플 집합 $d_r$이 삭제될 때

  • d_r의 각 튜플 t에 대해 V에서 그룹 t.A를 찾고 그룹 수에서 1을 뺀다.

  • 만약 카운트가 0이되면, 그룹 t.A에 대한 튜플을 v에서 삭제한다.

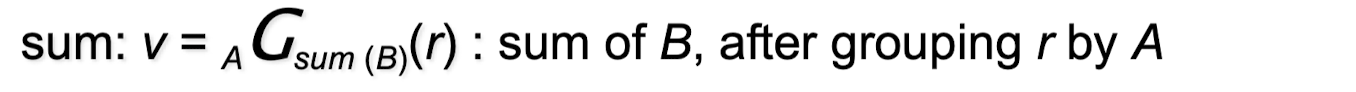
• 카운트에 대해 1을 더하거나 빼는 대신 B 값을 더하거나 빼는 것을 제외하면 count와 유사한 방식으로 합계를 유지한다.

• 또한 튜플이 없는 그룹을 감지하기 위해 개수를 유지한다. 이러한 그룹은 v에서 삭제된다.

• 단순히 sum = 0 인지 테스트할 수 없다.

Aggregation Operations (Cont.)

• avg 의 경우를 처리하기 위해 합계를 유지하고 집계 값을 개별적으로 카운트하고 마지막에 나눈다.

• r에 삽입을 처리하는 것은 간단하다.

• 삭제 시 집계 값 min 및 max를 유지하는 것이 더 비쌀 수 있다.

• e.g., 그룹의 최솟값이 삭제되면 동일한 그룹에 있는 r의 다른 튜플을 확인하여 새로운 최솟값을 조정해야한다.

Other Operations

• 집합 교집합 v = r ∩ s

  • 튜플이 r에 삽입되면 튜플이 s에 있는지 확인하고 있으면 v에 추가한다.

  • 튜플에서 r이 삭제되면 그리고 만약 교집합에 있으면 삭제한다.

  • s도 대칭적으로 업데이트 한다.

  • 다른 집합 연산, 합집합 및 차집합은 유사한 방식으로 처리된다.

• outer join은 join과 거의 같은 방식으로 처리되지만 약간의 추가 작업이 필요하다.

Handling Expressions

• 전체 식을 처리하기 위해 가장 작은 하위 식부터 시작하여 각 하위 식의 결과에 대한 증분 변화를 계산하기 위한 식을 파생한다.

• e.g.) E1, E2가 복합 표현식일 때, E1 ⋈ E2를 고려해보자.

  • E1에 삽입될 튜플 집합이 D1에 의해 주어진다고 가정하자.

  • 그러면 E1 ⋈ E2에 삽입될 튜플 세트는 D1 ⋈ E2 로 정의된다.

    • 이것은 조인을 유지하는 일반적인 방법이다.

Query Optimization and Materialized Views

• 구체화된 뷰를 사용하도록 쿼리 재작성:

  • 구체화된 뷰 v = r ⋈ s를 사용할 수 있다.

  • 사용자가 쿼리 r ⋈ s ⋈ t를 제출한다.

  • 쿼리를 v ⋈ t로 다시 작성할 수 있다.

    • 그렇게 할 것인지 여부는 두 가지 대안에 대한 비용 추정치에 따라 다르다.

• 구체화된 뷰의 사용을 뷰 정의로 대체한다.

  • 구체화된 뷰 v = r ⋈ s를 사용할 수 있지만 인덱스가 없다.

  • 사용자가 쿼리 $σ_{A=10}(v)$ 를 제출한다.

  • 또한 s가 공통 속성 B에 대한 인덱스를 갖고 있고 r이 속성 A에 대한 인덱스를 가지고 있다고 가정한다.

  • 이 쿼리에 대한 최상의 계획은 v를 r ⋈ s로 바꾸는 것일 수 있으며, 이는 쿼리 계획 $σ_{A=10}(r)⋈ s$ 로 이어질 수 있다.

• 위의 모든 대안을 고려하고 최상의 전체 계획을 선택하도록 쿼리 최적화 프로그램을 확장해야 한다!

Materialized View Selection

• Index selection: “생성하기에 가장 좋은 인덱스 세트는 무엇인가”

  • 구체화된 뷰 선택과 밀접하게 관련되지만 더 간단하다.

• materialized view selection: “ 구체화하기 가장 좋은 뷰 세트는 무엇인가”

• 일반적인 시스템 워크로드(쿼리 및 업데이트)를 기반으로 인덱스 선택 및 구체화된 뷰 선택

  • 일반적인 목표: 일부 중요한 쿼리 / 업데이트에 소요되는 공간 및 시간 제약에 따라 워크로드 실행 시간을 최소화하기.

  • 데이터베이스 튜닝 단계 중 하나

• 상용 데이터베이스 시스템은 데이터베이스 관리자가 생성할 인덱스와 구체화된 보기를 선택하는데 도움이 되는 도구 (”tuning assistants” or “wizards”)를 제공한다.