Query Optimization

Basic Concepts

• 주어진 쿼리를 평가하는 다른 방법

  • 동등한 표현

  • 작업마다 다른 알고리즘

Basic Concepts (Cont.)

• 평가 계획 (실행 계획)은 각 작업에서 사용되는 알고리즘과 작업 실행이 조정되는 방식을 정확히 정의한다.

Basic Concepts (Cont.)

• 쿼리에 대한 평가 계획 간의 비용 차이가 엄청 날 수 있다.

  • e.g.) 경우에 따라 seconds vs. days

• 비용 기반 쿼리 최적화 단계

  1. 동치 규칙을 사용하여 논리적으로 동등한 식을 생성한다. (여러 개의 relational algebra 생성)

  2. 결과 식에 주석을 달아 대체 쿼리 계획을 얻는다

  3. 예상 비용을 기준으로 가장 저렴한 계획을 선택한다.

• 계획 비용의 추정

  • relation에 대한 통계 정보

    • 튜플 수, 속성에 대한 고유 값의 수

  • 중간 결과에 대한 통계 추정

    • 복잡한 표현식의 비용 계산

  • 통계를 사용하여 계산된 알고리즘의 비용 공식

Transformation of Relational Expressions

• 두 relaitonal algebra 식이 모든 적법한 데이터베이스 인스턴스에서 동일한 튜플 세트를 생성하는 경우 두 relational algebra 표현식이 동등하다고 한다.

  • 참고: 튜플의 순서는 관련 없다.

• SQL 에서, 입력과 출력은 튜플의 다중 집합이다.

  • relational algebra의 다중 집합 버전에 있는 두 표현식은 두 식이 모든 유효한 데이터 베이스 인스턴스에서 동일한 다중 집합 튜플을 생성하는 경우 동등하다고 한다.

• 등가 규칙(equivalence rule)은 두 형식의 표현이 동등하다고 말한다.

  • 첫 번째 형식의 표현을 두 번째 형식으로 바꾸거나 그 반대로 바꿀 수 있다.

Equivalence Rules

1. conjunctive selection 연산은 일련의 개별 selection으로 분해될 수 있다.

   $σ_{θ1∧θ2}(E) = σ_{θ1}(σ_{θ2}(E))$

2. selection 연산은 교환법칙이 성립한다.

   $σ_{θ1}(σ_{θ2}(E)) = σ_{θ2}(σ_{θ1}(E))$

3. 일련의 projection 작업 중 마지막 작업만 필요하며 나머지는 생략할 수 있다.

   $π_{L1}(π_{L2}(...π_{Ln}(E))...)) = π_{L1}(E)$

4. selection은 Cartesian product 및 세타 조인과 결합될 수 있다.

   $σ_θ(E_1 X E_2) = E1 ⋈_θ E_2$

   $σ_{θ1}(E_1 ⋈_{θ2} E_2) = E1 ⋈_{θ1∧θ2} E_2$

5. 세타 조인 연산(그리고 natural join)은 교환법칙이 성립한다.

   $E_1 ⋈_θ E_2 = E_2 ⋈_θ E_1$

6. (a) natural join 연산은 결합 법칙이 성립한다.

   $(E_1 ⋈ E_2) ⋈ E_3 = E_1 ⋈ (E_2 ⋈ E_3)$

   

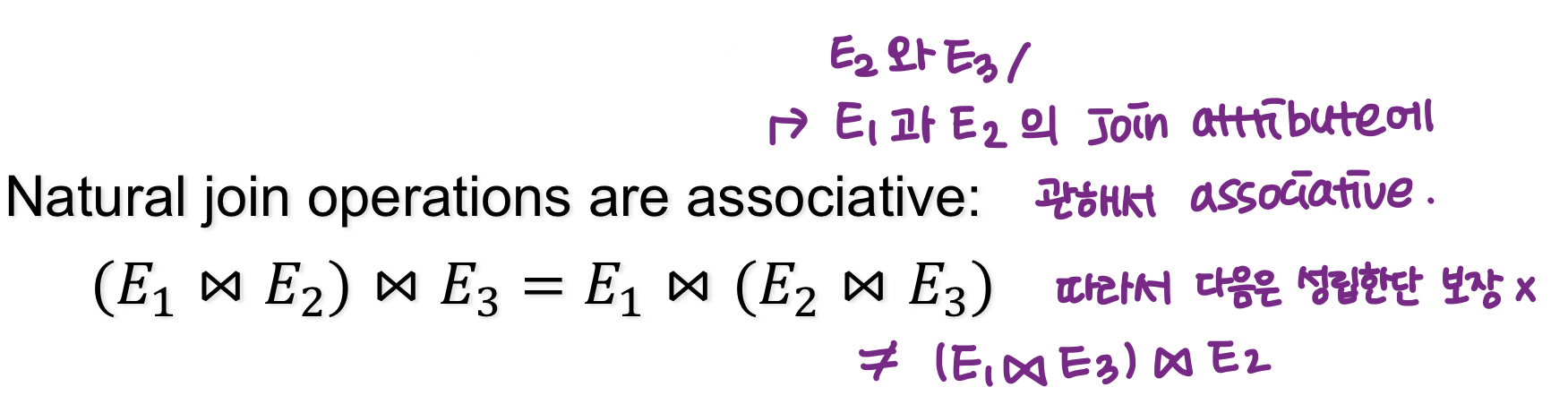
(b) 세타 조인은 다음과 같은 방식으로 결합된다.

$(E_1 ⋈_{θ1} E_2)⋈_{θ2∧θ3}E_3 = E_1 ⋈_{θ1∧θ3} (E_2 ⋈_{θ2} E_3)$

→ 여기서 $θ_2$ 는 오직 $E_2$ 와 $E_3$ 의 속성만을 포함한다.

Pictorial Depiction of Equivalence Rules

• 등가 규칙의 그림 묘사

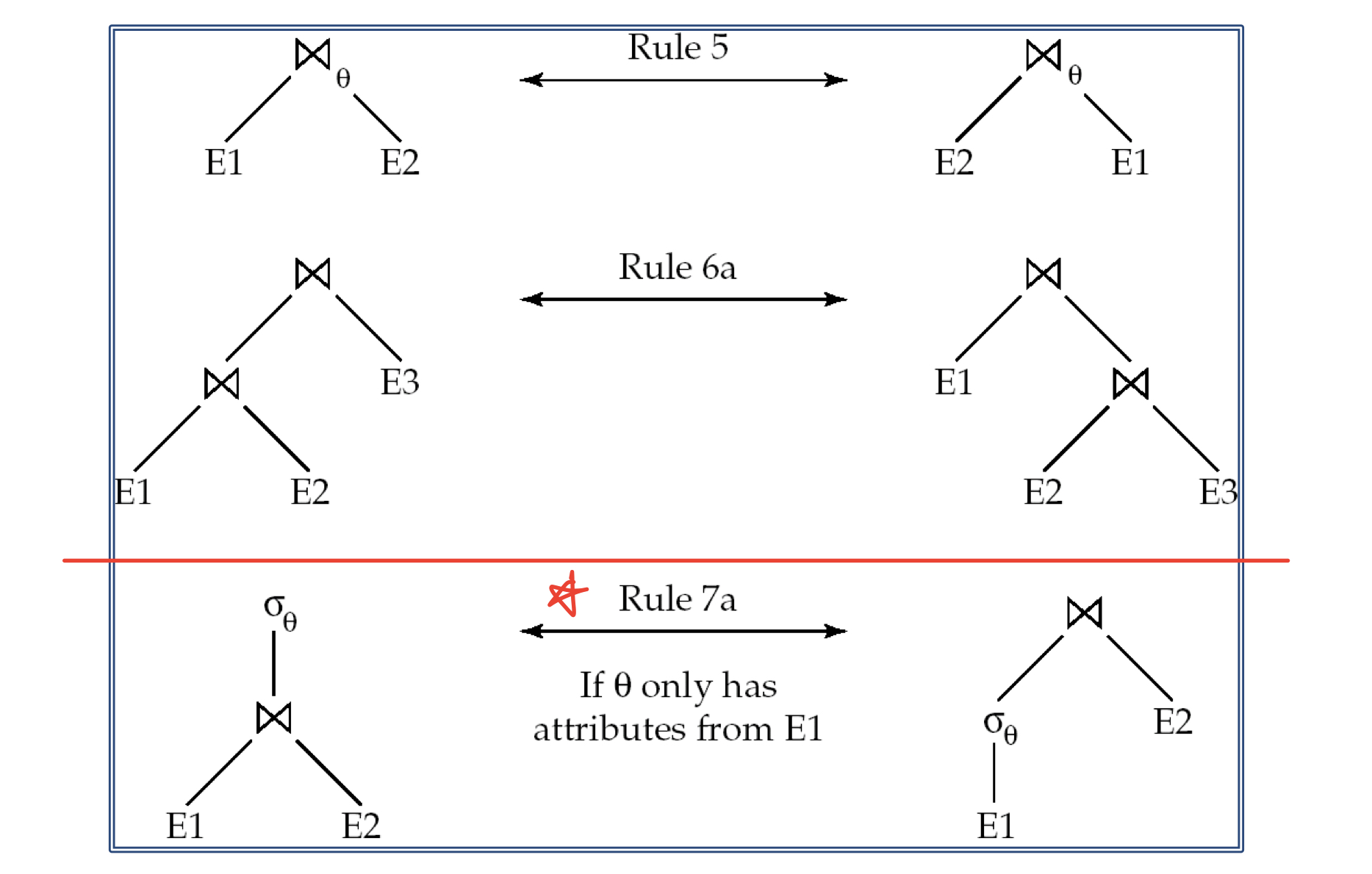
Equivalence Rules (Cont.)

1. selection 연산은 다음 두 가지 조건에서 세타 조인 연산을 통해 분배된다.

   1. $θ_0$ 의 모든 속성이 조인되는 식 (E1) 중 하나의 속성만 포함하는 경우

   $σ_{θ_0}(E_1 ⋈_{θ} E_2) = (σ_{θ_0}(E_1)) ⋈_{θ} E_2$

   

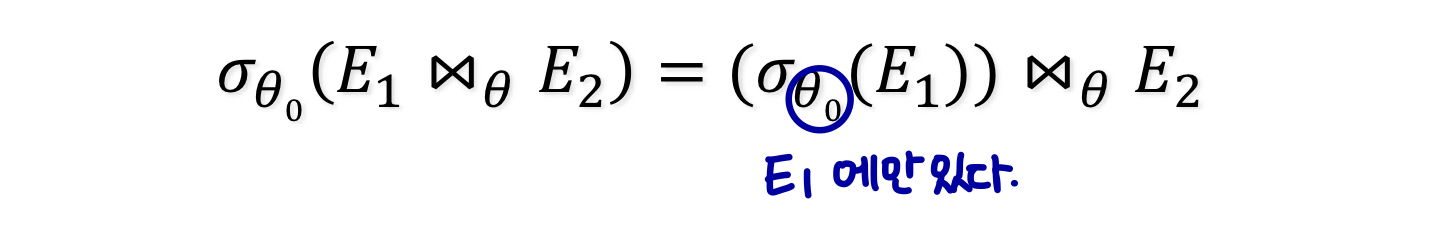
   b. $θ_1$이 E1의 속성만 포함하고 $θ_2$가 E2의 속성만 포함하는 경우

   $σ_{θ_1∧θ_2}(E_1 ⋈_{θ} E_2) = (σ_{θ_1}(E_1)) ⋈_{θ} (σ_{θ_2}(E_2))$

Equivalence Rules (Cont.)

1. projection 연산은 세타 조인 연산에 다음과 같이 분배된다.

   1. θ가 $L_1 ∪ L_2$의 속성만 포함하는 경우:

   $π_{L1∪L2}(E_1 ⋈_{θ} E_2) = π_{L1}(E_1))⋈_{θ} ( π_{L2}(E_2)))$

   L1과 L2는 각각 E1와 E2의 속성 집합이다.

   b. $E_1 ⋈_{θ} E_2$ join 고려

   • L1과 L2는 각각 E1과 E2의 속성 집합이다.

   • L3은 조인 조건 θ에 포함되지만 L1 ∪ L2에는 없는 E1의 속성이라고 하고

   • L4는 조인 조건 θ에 포함되지만 L1 ∪ L2에는 없는 E2의 속성이라고 하자

   $π_{L_1∪L_2}(E_1 ⋈_{θ} E_2) = π_{L_1∪L_2}((π_{L_1∪L_3}(E_1))⋈_{θ} (π_{L_2∪L_4}(E_2))$

1. 합집합과 교집합은 교환법칙이 성립한다.

   $E_1 ∪ E_2 = E_2 ∪ E_1$

   $E_1 ∩ E_2 = E_2 ∩ E_1$

(집합에서 차집합은 교환법칙이 성립하지 않는다)

1. 합집합과 교집합은 결합법칙이 성립한다.

   $(E_1 ∪ E_2)∪ E_3 = E_1 ∪ (E_2 ∪ E_3)$

   $(E_1 ∩ E_2) ∩ E_3 = E_1 ∩ (E_2 ∩ E_3)$

2. selection 연산은 ∩, ∪ 및 -에 걸쳐 분배된다.

   $σ_{θ}(E_1 - E_2) = σ_{θ}(E_1) - σ_{θ}(E_2)$

3. projection 연산은 합집합을 통해 분배된다.

   $π_{L_1}(E_1 ∪ E_2) = π_{L_1}(E_1))∪π_{L_2}(E_2))$

Transformation Example: Pushing Selections

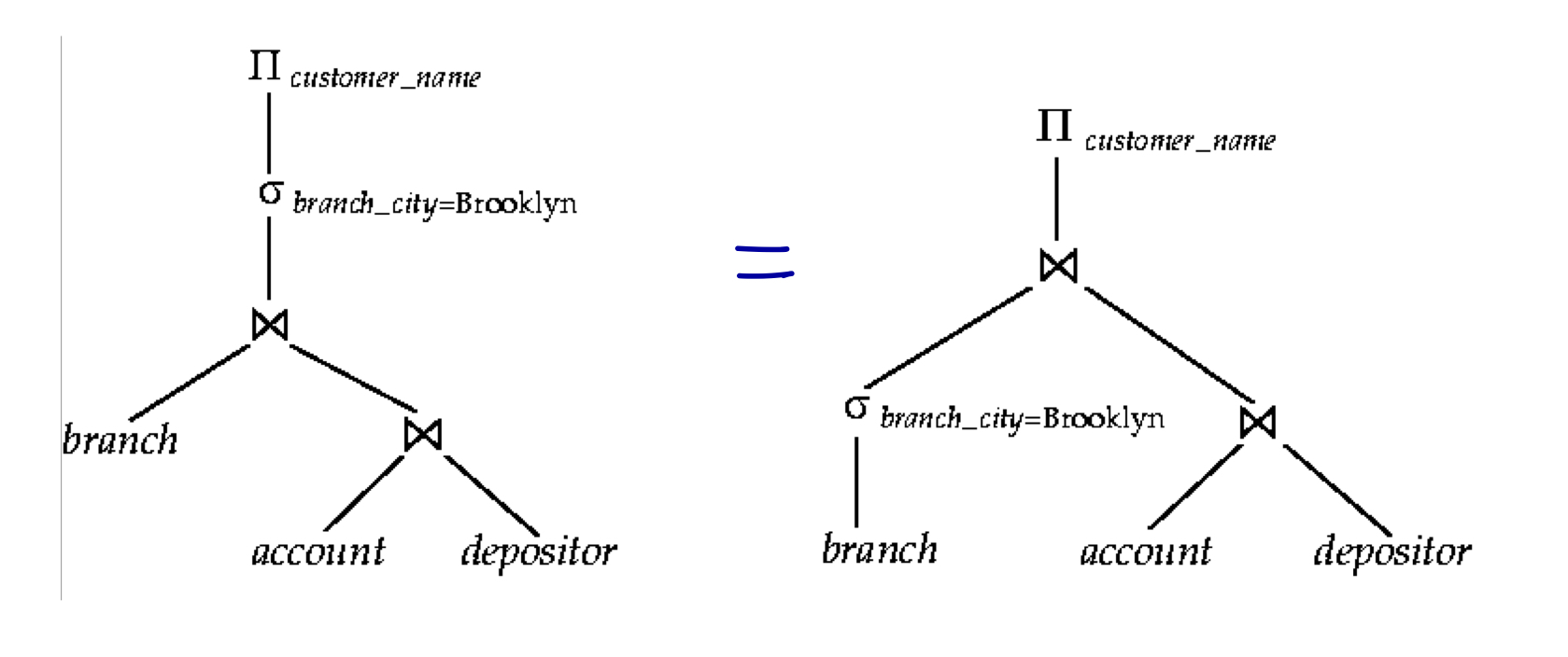
• Query: Brooklyn에 위치한 몇몇 지점에 계좌를 갖고 있는 모든 고객의 이름을 찾아라.

  $π_{customer-name}(σ_{branch-city="Brooklyn"}(branch ⋈ (account ⋈ depositor)))$
  

• 규칙 7a에 의해 변형

  $π_{customer-name}((σ_{branch-city="Brooklyn"}(branch)) ⋈ (account ⋈ depositor)))$
  

• 가능한 한 빨리 selection을 수행하면 조인할 relation의 크기가 줄어든다.

Example with Multiple Transformations

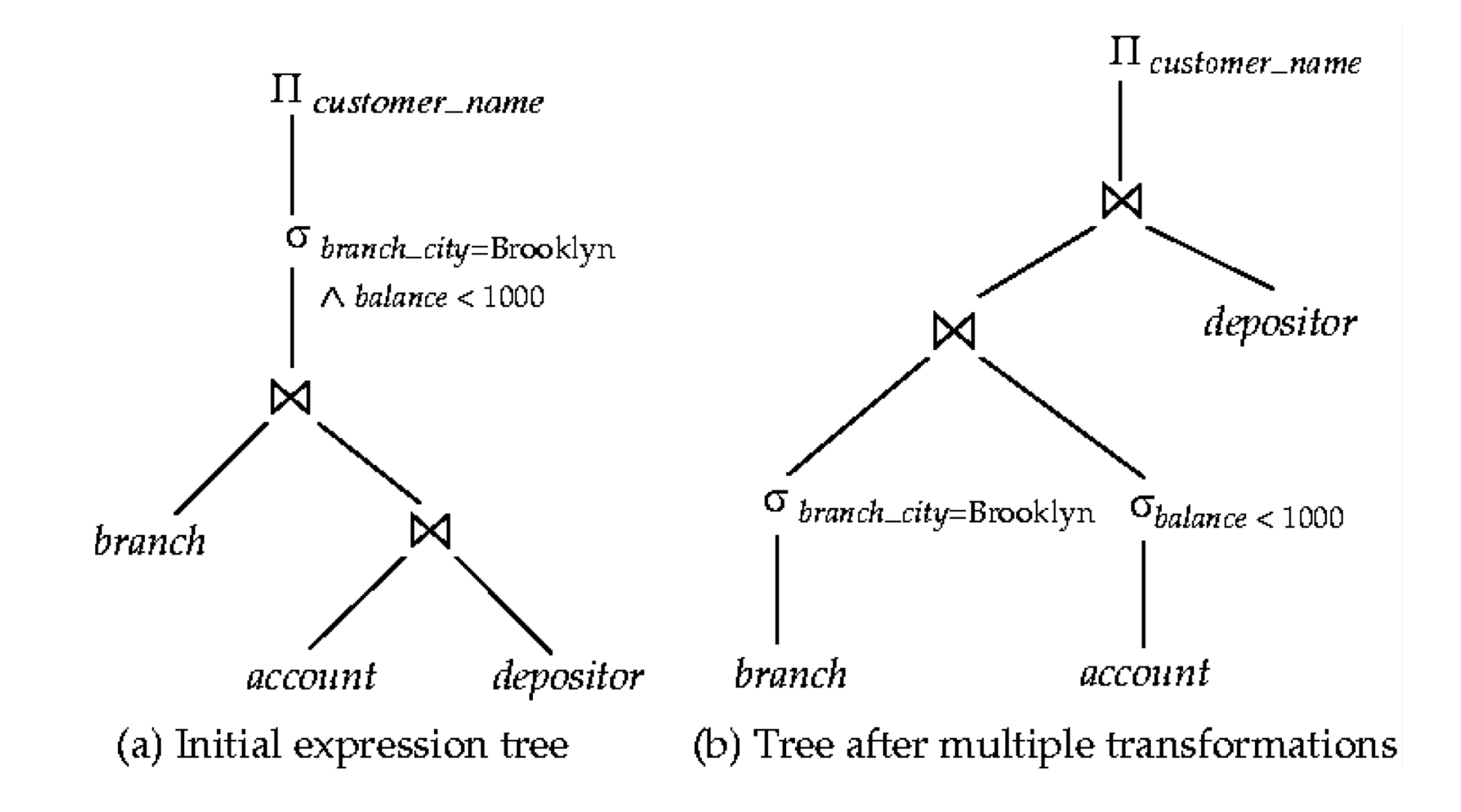
• Query: 계좌 잔고가 1000달러가 넘는 Brooklyn 지점에 계좌가 있는 모든 고객의 이름을 찾아라.

  $π_{customer-name}((σ_{branch-city="Brooklyn"∧balance>1000}(branch ⋈ (account ⋈ depositor)))$
  

• 규칙 6a을 적용해 join 결합 법칙을 사용하여 변형

  $π_{customer-name}((σ_{branch-city="Brooklyn"∧balance>1000}(branch ⋈ account)) ⋈ depositor)$
  

• 두 번째 형식은 “일찍 selection 수행” 규칙을 적용할 수 있는 기회를 제공하여 하위 표현을 생성한다. (규칙 7b)

  $σ_{branch-city="Brooklyn"}(branch) ⋈σ_{balance>1000}(account)$
  

• 따라서 일련의 변환이 유용할 수 있다.

Multiple Transformations (Cont.)

Transformation Example: Pushing Projections

$π_{customer-name}((σ_{branch-city="Brooklyn"}(branch) ⋈ account) ⋈ depositor)$

• $(σ_{branch-city="Brooklyn"}(branch) ⋈ account)$ 를 계산할 때, 우리는 다음의 스키마를 포함하는 relation을 얻는다. (branch-name, branch-city, assets, account-number, balance)
  

• 등가 규칙 8a와 8b를 사용하여 projection을 수행한다.

• projection을 가능한 빨리 수행하면 조인할 relaion의 크기가 줄어든다.

Join Ordering Example

• 모든 relation r1, r2, r3에 대해 $(r_1⋈r_2)⋈r_3 = r_1⋈(r_2⋈r_3)$ (Join Associativity) 결합법칙
  

• 만약 $r_2⋈r_3$ 은 꽤 크고 $r_1⋈r_2$ 가 작으면, 우린 더 작은 임시 relation을 계산하고 저장하기 위해 다음을 선택한다. $(r_1⋈r_2)⋈r_3$
  

Join Ordering Example (Cont.)

• 다음 표현식을 고려해보자.

  $π_{customer-name}((σ_{branch-city="Brooklyn"}(branch)) ⋈ (account ⋈ depositor)))$
  

• account ⋈ depositor를 먼저 계산하고 join한 결과에 다음을 수행할 수 있다.

  $σ_{branch-city="Brooklyn"}(branch)$

  하지만 account ⋈ depositor 은 큰 relation일 확률이 높다.
  

• 은행 고객 중 극히 일부만이 Brooklyn에 위치한 지점에 계좌를 가지고 있을 가능성이 높다.

  $σ_{branch-city="Brooklyn"}(branch)⋈account$

  이 연산을 먼저하는 것이 훨씬 낫다.
  

Enumeration of Equivalent Expressions

• 쿼리 최적화 프로그램(query optimizer)은 동등성 규칙을 사용하여 주어진 식과 동등한 식을 체계적으로 생성한다.

• 다음과 같은 모든 동등한 표현식을 생성할 수 있다:

  반복

  지금까지 발견된 모든 동등한 표현에 적용 가능한 동등성 규칙을 적용한다.

  새로 생성된 표현식을 동등한 표현식 세트에 추가한다.

  위에서 새로운 등가 표현이 생성되지 않을 때 까지
  

• 위의 접근 방식은 공간과 시간이 매우 비싸다.

  • 두 가지 접근 방식

    • 변환 규칙에 따라 최적화된 계획 생성

    • selection, projection 및 join만 있는 쿼리에 대한 특수 사례 접근 방식

Cost Estimation

• 앞서 설명한 대로 계산된 각 연산자의 비용

  • 입력 relation의 통계가 필요

  • e.g.) 튜플 수, 튜플 사이즈

• 입력은 하위 표현식(sub-expression)의 결과일 수 있다.

  • 표현식 결과의 통계를 추정해야 한다.

  • 이를 위해서는 추가 통계가 필요하다.

    • e.g.) 속성에 대한 고유 값의 수

• 나중에 비용 추정에 대해 자세히 알아볼 것이다!

Choice of Evaluation Plans

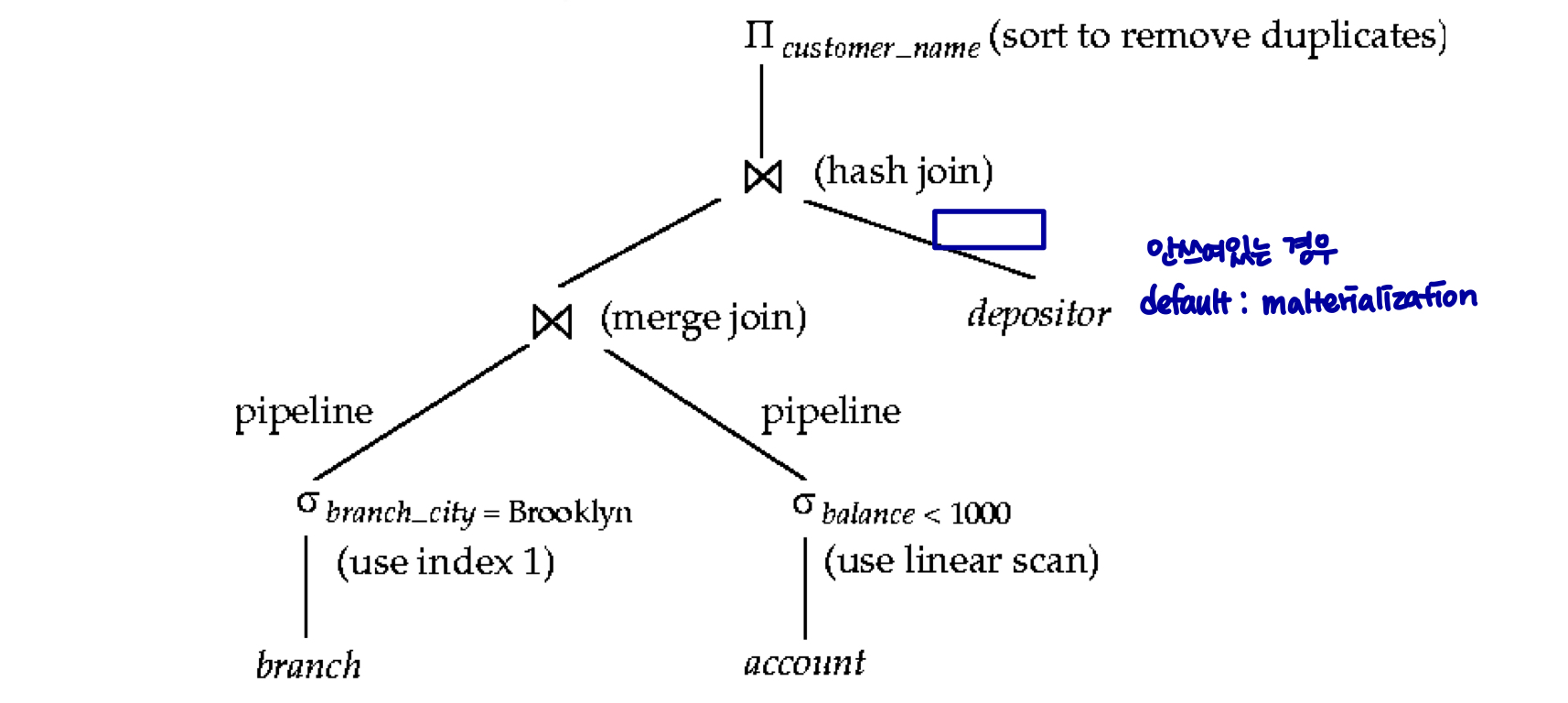
• 평가 계획을 선택할 때, 평가 기술의 상호작용을 고려해야 한다.

  • 각 작업에 대해 가장 저렴한 알고리즘을 독립적으로 선택하면 최상의 전체 알고리즘이 생성되지 않을 수 있다. e.g.) 병합 조인은 해시 조인보다 비용이 많이 들 순 있지만 외부 level 집계 비용을 줄이는 정렬된 출력을 제공할 수 있다. nested-loop 조인은 파이프라인을 위한 기회를 제공할 수 있다.
    

• 실용적인 쿼리 최적화 프로그램은 다음 두 가지 광범위한 접근 방식의 요소를 통합한다.

  1. 모든 계획을 탐색하고 비용 기반 방식으로 최상의 계획을 선택한다.
  2. 휴리스틱을 사용하여 계획을 선택한다.

Cost-Based Optimization

• 최상의 조인 순서를 찾는 것을 고려한다.

  ($r_1⋈r_2⋈r_3...⋈r_n.$)
  

• 위 식에서의 조인 순서 2(n-1)!/(n-1)!

  n=7 이면 665280이고, n=10이면 숫자는 1760억 보다 크다.
  

• 모든 조인 순서를 생성할 필요가 없다. 동적 프로그래밍을 사용하면 { ${r_1, r_2, ..., r_n}$} 의 하위 집합에 대한 최소 비용 조인 순서가 한 번만 계산되고 나중에 사용할 수 있도록 저장된다.

• e.g.) $(r_1⋈r_2⋈r_3)⋈r_4⋈r_5$

Heuristic Optimization

• 비용 기반 최적화는 비용이 많이 든다.

• 시스템은 휴리스틱을 사용하여 비용 기반 방식으로 선택해야 하는 선택의 수를 줄일 수 있다.

• 휴리스틱 최적화는 일반적으로 (모든 경우는 아니지만) 실행 성능을 향상시키는 일련의 규칙을 사용하여 쿼리 트리를 변환한다.

  • 조기에 selection 수행 (튜플 수를 줄임)

  • 조기에 projection 수행 (속성 수를 줄임)

  • 다른 유사한 작업보다 먼저 가장 제한적인 selection과 join 작업(즉, 결과 크기가 가장 작은)을 수행한다.

  • 일부 시스템은 휴리스틱만 사용하고 다른 시스템은 휴리스틱과 부분 비용 기반 최적화를 결합한다.