Basic concepts
-
Database Design
-
어떤 테이블을 만들 것인가?
-
각 테이블은 어떤 attribute를 가지게 할 것인가?
-
-
목표: 불필요한 중복(redundancy)없이 필요한 정보를 모두 표현(저장)할 수 있는 schema.
⇒ 어떤 attribute를 갖는 어떤 table을 둘 것인가?
R = (A B C D E) ← signle relation schema 정의
DB1 = {R1, …. , Rn} ← DB schema 정의 (set of relation schemas)
-
문제점
-
동일한 문제에 대해서 여러 가지 디자인이 가능하다.
-
어떤 것이 더 좋은 디자인인가? 왜 더 좋은 디자인인가?
-
제 1 정규형 (1NF)
-
정규형이란 정규화된 결과를 말하며, 제 1 정규형, 제 2정규형, 제 3 정규형. BCNF가 있다 .
-
도메인의 요소들이 분리 불가능한 units으로 구성되어있으면 해당 도메인은 atomic 하다고 표현한다.
-
non-atomic 한 도메인의 예시
-
이름의 집합, 복합 속성
-
한 컬럼의 값이 (원필, 도운) 으로 되어 있는 경우, 여러 부분으로 나눌 수 있는 cs101과 같은 식별 번호 (CS101)
-
원필, 도운 is divisible into 원필/도운
-
CS101 is divisible into CS, 101
-
-
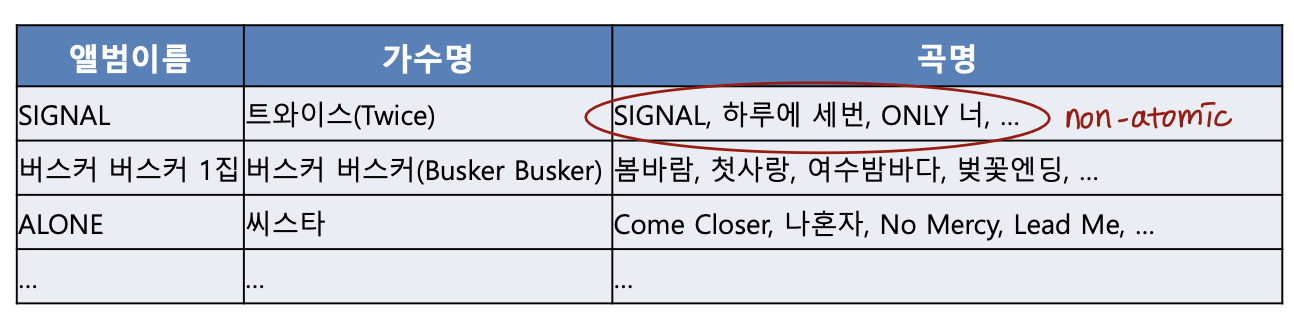
제 1 정규형은 릴레이션에 속하는 속성의 속성 값이 모두 원자값(Atomic Value)만으로 구성되어야 한다. (원자값이란 더 이상 쪼개질 수 없는 단위를 말한다.)
Non-atomic attributes
- 데이터베이스에서가 아닌 응용 프로그램에서의 정보 인코딩을 이끌 수 있다.
- 복잡한 저장과 쿼리 processing, 정보의 중복된 저장을 이끈다.
- 예) 각 고객마다 저장된 계좌정보에 그 계좌를 소유한 오너의 집합이 함께 저장될 경우.
-
원자성은 실제로 도메인의 요소가 사용되는 방식의 속성이다.
-
예) 문자열은 보통 indivisible하다고 간주된다.
-
학생들에게 CS0012 또는 EE1127 문자열의 롤 번호가 주어진다고 가정해보자.
-
만약 첫 두 문자가 학과를 찾아내는데 추출된다면 해당 롤 번호 도메인은 atomic 하지 않다.
-
이런 방식은 bad idea이다. → 데이터베이스가 아닌 응용 프로그램에서의 정보 인코딩을 이끌기 때문이다. (바꿔 말하면, 단순히 DB 접근만을 통해서 완벽하게 데이터의 정보를 알 수 없다)
-
Pitfalls in Relational Database Design
-
Relational database design: 필요한 정보를 위한 릴레이션 스키마의 “좋은” 집합을 찾는 것이다.
-
A bad design may lead to
-
특정 정보를 나타낼 수 없음
-
정보의 중복
-
정보의 손실
-
-
Design Goals:
-
attributes사이의 관계가 잘 나타나도록 보장해야한다. (information content)
-
정보의 중복을 피해야한다.
-
database 참조 무결성 제약 조건의 시행을 용이하게 한다.
-
Database Design Goal
-
나쁜 디자인
-
특정 정보를 나타낼 수 없다
-
정보의 중복
-
정보의 손실
-
Anomaly (이상)
- 갱신 이상 (Update anomaly)
- 삭제 이상 (Deletion anomaly)
- 삽입 이상 (Insertion anomaly)
-
-
좋은 디자인
-
attribute 사이의 관계를 표현한 수 있도록 보장해야한다. (information content)
-
정보의 중복(redundancy)를 피해야한다.
-
데이터베이스 무결성 제약 조건 보장을 용이하게 한다.
-
Database Design Goal - Example
Leading-schema = (branch-name, branch-city, assets, customer-name, loan-number, amount)
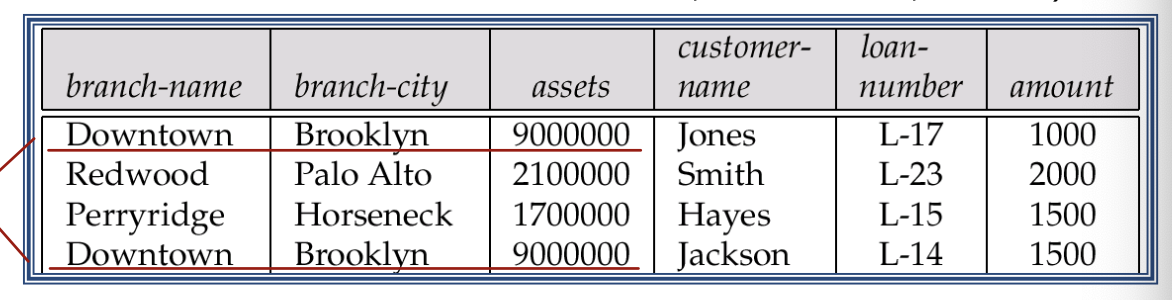
-
Redundancy
-
branch-name, branch-city, assets의 데이터는 해당 branch가 만들어낸 각 계좌를 나타낼때 중복된다.
-
공간을 낭비한다.
-
업데이트를 복잡하게 만들고, assets 값의 불일치성의 가능성을 도입한다.
-
-
Null value
-
만약 계좌가 존재하지 않는다면 해당 branch에 관한 정보를 저장할 수 없다.
-
이 경우, null 값을 사용할 순 있지만 null 값이 들어가면 데이터를 다루기 어려워진다.
-
Anomaly
-
Anomalies (by Codd)
-
Insertion anomaly: loan-number 없이 branch 정보 insert 불가능
-
Deletion anomaly: 어떤 branch의 단 하나뿐인 acount를 삭제할 경우 해당 branch 정보를 확인할 수 없다.
-
Update anomaly: 일부는 업데이트하고 일부는 안될 가능성이 있다. 해당 data를 포함하는 행을 모두 찾아내 update 해야한다.
-
-
원인
-
정보의 중복 (Redundancy)
-
여러 entity가 하나의 table에 합쳐짐
-
-
해결책: Decomposition !!
Decomposition
-
Definition
-
R을 relational sheme이라고 하자.
-
만약 R = R1 U … U Rn (즉, 모든 attribute가 R1, … , Rn에 존재하면)
{R1, …. , Rn}은 R의 decomposition 이다.
-
-
우리는 주로 binary decomposition을 다룰 것이다.
-
R into {R1, R2} where R = R1 U R2

Decomposition - Examples
-
학생 (학번, 이름, 학과, 학과장, 학과전화, 학년) R
⇒ 학생 (학번, 이름, 학년, 학과) R1
학과 (학과, 학과장, 학과전화) R2
- R = R1 U R2
-
Leading = (b_name, b_city, asset, loan#, c_name, amount)
⇒ Branch = (b_name, b_city, asset) R1
Loan = (loan#, c_name, amount) R2-
R = R1 U R2
-
decomposition 하긴 했는데, 관계가 없어졌다.
-
어느지점에서 어떤 사람이 대출했는지 알 수 없다. ⇒ connection trap!
-
상관관계가 없어졌다.
-
큰 틀에서 보면 정보의 손실(loss of information)이 발생했다.
-
즉, Lossy decomposition.
-
Lossy Decomposition
- Lending = (b_name, b_city, asset, loan#, c_name, amount) : 정보의 중복 때문에 anomaly가 발생한다.

제대로 decomposition 하면 다음과 같다.
- Branch (b_name, b_city, asset)
- Loan (loan#, c_name, amount, b_name)
A Lossy Decomposition
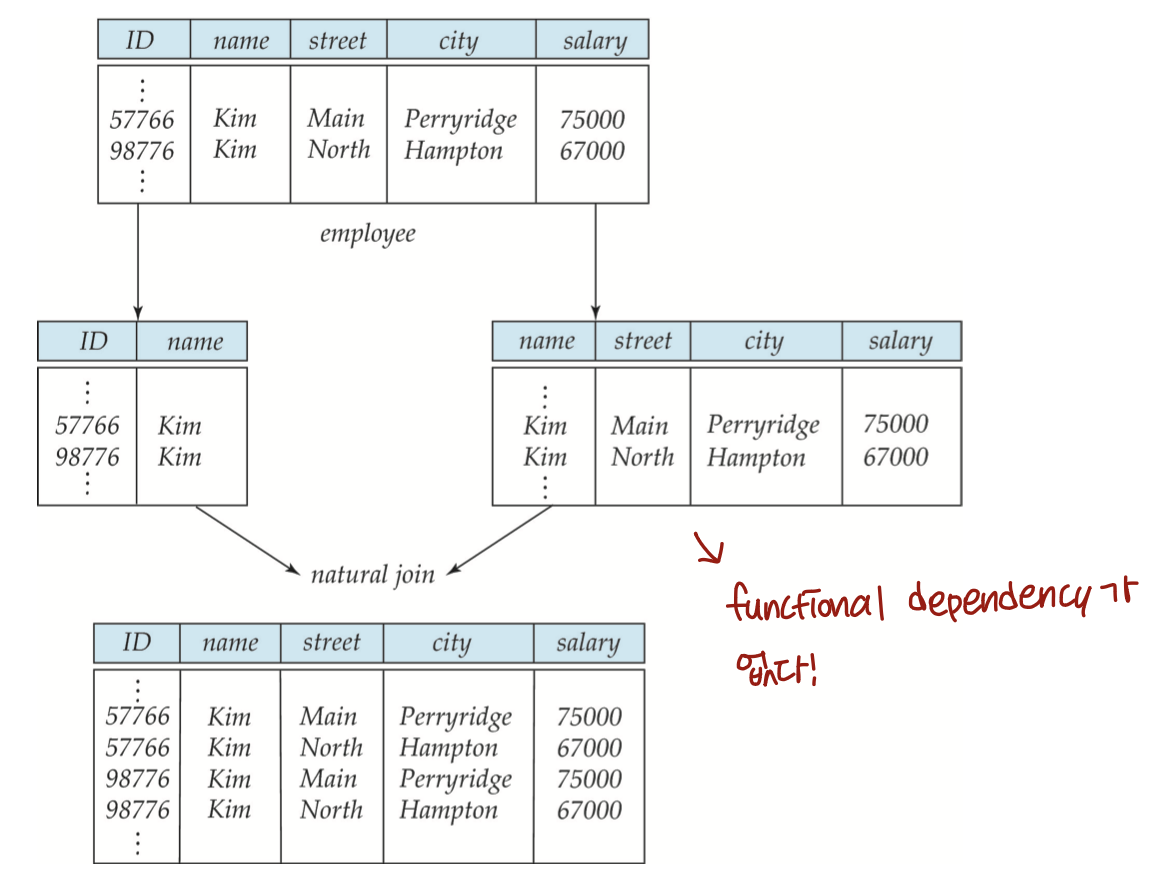
Example of Lossless-Join Decomposition
- Lossless join decomposition
- Decomposition of R = (A, B, C) → R1 = (A, B); R2 = (B, C)
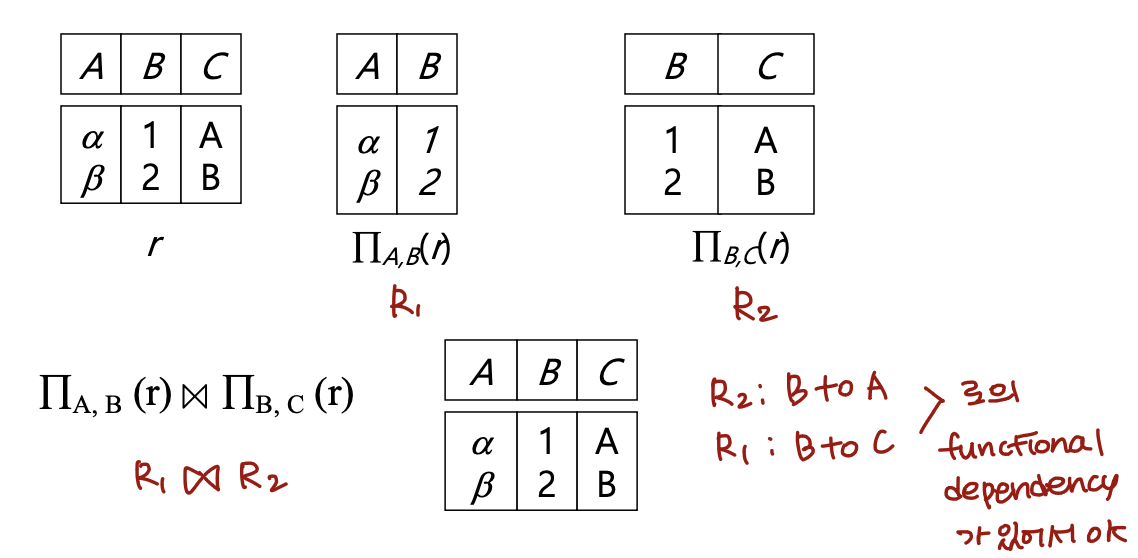
Lossless-join Decomposition
-
부주의한 decomposition은 정보의 손실을 이끈다.
- 잘못된 연결 attributes 설정 (Lossy decomposition)
-
r(R)이 있고 decomposition {R1, R2} 가 있을 때, R1과 R2의 교집합이 공집합이 아니면,
r ⊆ πR1(r) ⋈ πR2(r) 이다.
-
정의:
Decomposition {R1, R2} 는
만약 r = πR1(r) ⋈ πR2(r) 라면 lossless-join decomposition 이다.
-
기준 information은 원래의 r의 information이다.
보완할 부분이 있으면 댓글 남겨주세요. :)
