Functional Dependency (1)

Goal

• 특정 릴레이션 R이 “좋은” 형태인지아닌지 결정하다.

• 릴레이션 R이 “좋은”형태가 아닌 경우, 이것을 {R1, R2, … , Rn}의 릴레이션 집합으로 분해한다.

  • 이때, 각각의 릴레이션이 좋은 형태이다.

  • decomposition이 lossless-join decomposition이다.

• 우리의 이론은 다음에 기초한다.

  • Functional dependency (함수 종속성)

  • multivalued dependencies (이에 대해선 다루지 않을 예정이다.)

Functional Dependencies

• α → β

  • α 는 함수적으로 β를 결정한다.

  • α, β: attributes의 집합

  • 동일한 α를 갖는 두 튜플은 동일한 β를 갖는다.

  • α가 주어(정해)지면 반드시 β가 정해진다.

  • α 값이 같은데 β 값이 다른 경우는 없다.

  • 함수적 종속성은 key(키) 개념의 일반화이다.

• 실제 application domain의 규칙/상황/Rule에 의하여 정해진다.

  • 학번 → 이름 ?? YES

  • 이름 → 학번 ?? NO

  • 주민등록번호 → 학번 ?? YES

• Relation의 모든 instance에서 이 규칙이 성립하여야 함

Functional Dependencies (Cont.)

• R이 relational schema이고 α ⊆ R, β ⊆ R이라고 하자.

• 어떤 합접적인 릴레이션 r(R)이 있고, attribute α에 동의하는 어떤 2개의 튜플 t1, t2가 있을 때,그 튜플은 attribute β에도 동의한다. 그 경우에만 functional dependency α→β는 R에 성립한다.

  즉, t1[α] = t2[α] ⇒ t1[β] = t2[β]

  

Applications of FD

• K → R 인 경우에만 K는 릴레이션 스키마 R의 super key이다.

• K → R, and

  for no α⊂K, α→R.

  인 경우에만 K 가 R의 key / candidate key 이다.
  

• functional dependencies는 super key를 사용해 표현할 수 없는 제약 조건들을 표현할 수 있도록 해준다.

  • Loan-info-schema = (customer-name, loan-number, branch-name, amount)

  • 다음의 functional dependencies들은 성립한다.

    • loan-number → amount
    • loan-number → branch-name

  • 다음은 성립하지 않는다.

    • loan-number → customer-name

      ( 하나의 계좌에 여러 명이 연결되어 있을 수 있기 때문이다.)

Applications of FD (cont.)

• 주의: functional dependency가 모든 합법적인 instance에서 성립하지 않을 지라도, relation schema의 특정 instance에서는 우연치 않게 functional dependency가 만족될 수 있다.

  • 예) Loan-schema의 특정 instance는 우연히 다음 FD를 만족할 수 있다.

    • loan-number → customer-name

  • 하지만 일반적인 경우에는 성립하지 않는다.

FD example

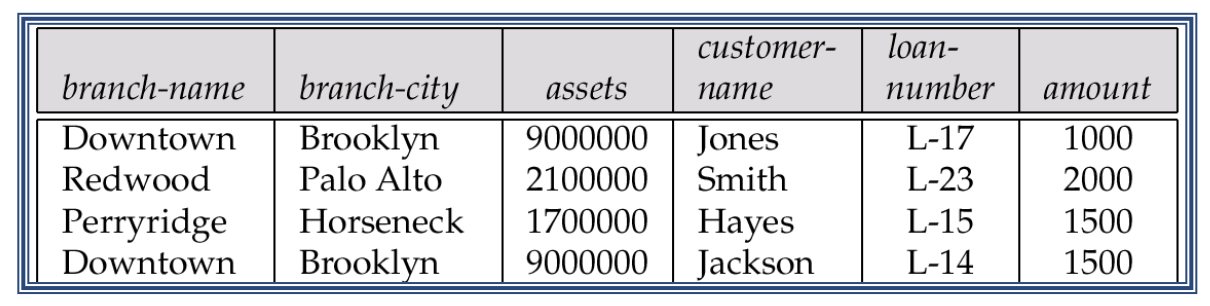
• loan-number → amount? YES
• loan-number → branch-name? YES
• loan-number → customer-name? NO
• branch-city → branch-name? NO
• branch-name → branch-city? YES
• branch-name → assets? YES

현재 상태에서만 참인 경우가 있으나 항상 참이 아닌 경우가 있을 수 있으므로 주의를 요한다!

FD example (cont.)

• 다음 스키마를 고려해보자.

  inst_dept(ID, name, salary, dept_name, building, budget)

  • 다음 functional dependencies가 성립함을 알 수 있다.

    • dept_name → building

    • and ID → building

    • 즉, dept_name, ID → building

    • 결정자가 super key여야마나 value의 repetition이 발생하지 않는다.

  • 하지만 다음은 성립하지 않는다.

    • dept_name → salary

    • 결정자가 super key가 아니기 때문이다.

Trivial FD

• 만약 functional dependency가 릴레이션의 모든 instance에서 만족된다면, 해당 functional dependency는 trivial 하다고 한다.

  • e.g.

    • customer-name, loan-number → customer-name
    • customer-name → customer-name

• 당연히! 성립할 수 밖에 없는 FD를 말한다.

  • e.g.

    • {이름, 나이} → {이름}
    • {나이} → {나이}
    • {나이} → ф
    • 심지어 ф → ф

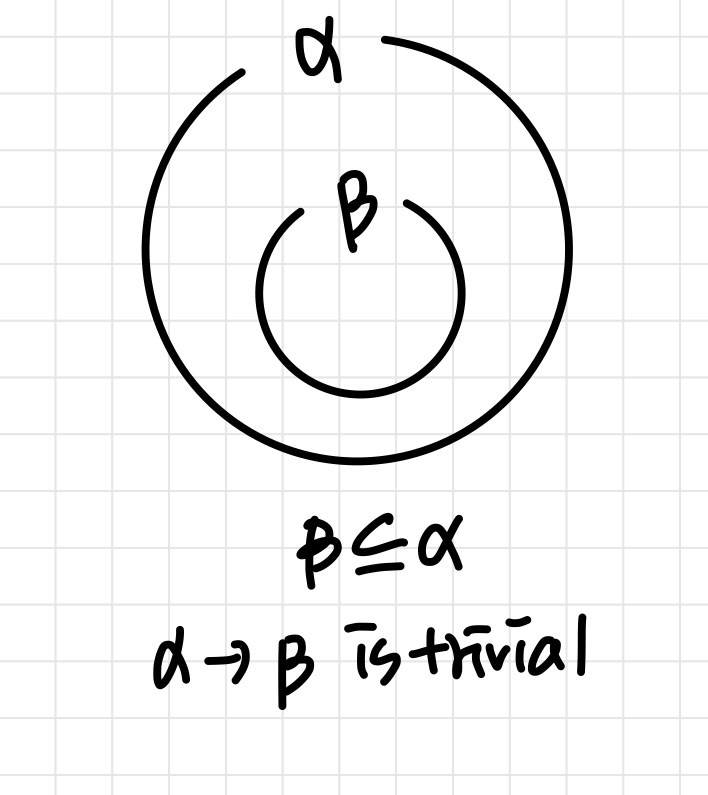
• β ⊆ α 인 경우, α → β 는 자명(trivial)하다.

Closure of a Set of FDs

• FD의 집합 F가 주어졌을 때, F에 의해 논리적으로 암시되는 특정 다른 FD가 있다.

  • e.g.

    if A → B and B → C, then we can infer that A → C

• F에 의해 논리적으로 추론되는 모든 functional dependency의 집합을 F의 closure라고 부른다.

• F의 closure는 F+로 나타낸다.

  • F+ is a super set of F.

Closure of a Set of FDs

• 암스트롱의 공리(Armstrong’s Axioms)를 적용해서 모든 F+를 찾아낼 수 있다.

  • (reflexivity) if β ⊆ α, α → β

    • e.g.) ABC → BC 추론 가능

  • (augmentation) if α → β, then γα → γβ (augmentation)

    • e.g.) AB → CD 일 때, ABE → CDE 추론 가능

  • (transitivity) if α → β, and β → γ, then α → γ

    • e.g.) A→ B 이고, B → C 이면 A → C 추론 가능

• transitivity는 다른말로 이행적 함수 종속이라고 부른다

• 암스트롱의 공리는 그 자체로 sound하고 complete 하다.

Example

• R = (A, B, C, G, H, I)

• F = { A → B, A → C, CG → H, CG → I, B → H)

• some members of F+

  • A→ H

    • A → B, B → H 를 transitivity 하면 A → H 를 이끌어낼 수 있다.

  • AG → I

    • A → C를 G로 augmentation 하면 AG → CG 이고, 이를 CG → I 와 transitivity 하면 AG → I 를 이끌어 낼 수 있다.
      

  • CG → HI

    • CG → I 를 CG로 augmentation 하면 CG → CGI 가 되고, 이를 위해 CG → H 를 I로 augmentation 하면 CGI → HI 가 된다. 이후 transitivity를 통해 CG → HI 를 이끌어 낼 수 있다.

    • 이 방식은 additional rule의 union rule을 통해 간소화될 수 있다.

Additional rules

• Additional rules:

  • (union rule) if α → β holds and α → γ holds, then α → βγ holds

    • e.g.) AB → BC 이고 AB → EF 이면 AB → BCEF 추론 가능

  • (decomposition) if α → βγ holds, then α → β holds and β → γ holds

    • e.g.) AB → CDEF 이면, AB → C, AB → D, AB → EF 등의 함수 종속 추론 가능

  • (pseudotransitivity) if α → β holds and γβ → δ holds, then αγ → δ holds

    • e.g.) AB → C 이고 CD → EF 이면 ABD → EF 추론 가능

• 위의 세가지 rule은 암스트롱의 공리에 의해 추론될 수 있다.

• 다음의 예제를 풀어보자

  릴레이션 스키마 R은 다음과 같고 R(A, B, C, D), 함수종속 F은 다음과 같다. F = {A→B, C→D}.  주어진 함수 종속을 이용하여 AC→BD가 추론 가능함을 보여라.

• 정답은 다음과 같다.

보완할 부분이 있으면 댓글 남겨주세요. :)