퍼셉트론

본 내용은 밑바닥부터 시작하는 딥러닝. 사이토 고키 저.를 참고하여 작성되었습니다.

퍼셉트론(Perceptron)은 프랑크 로젠블라트(Frank Rosenblatt)가 1957년에 제안한 초기 형태의 인공 신경망으로 다수의 입력으로부터 하나의 결과를 내보내는 알고리즘이다.

퍼셉트론은 신경망(딥러닝)의 기원이 되는 알고리즘이다. 그래서 퍼셉트론의 구조를 배우는 것은 신경망과 딥러닝으로 나아가는 데 중요한 아이디어를 배우는 일이다.

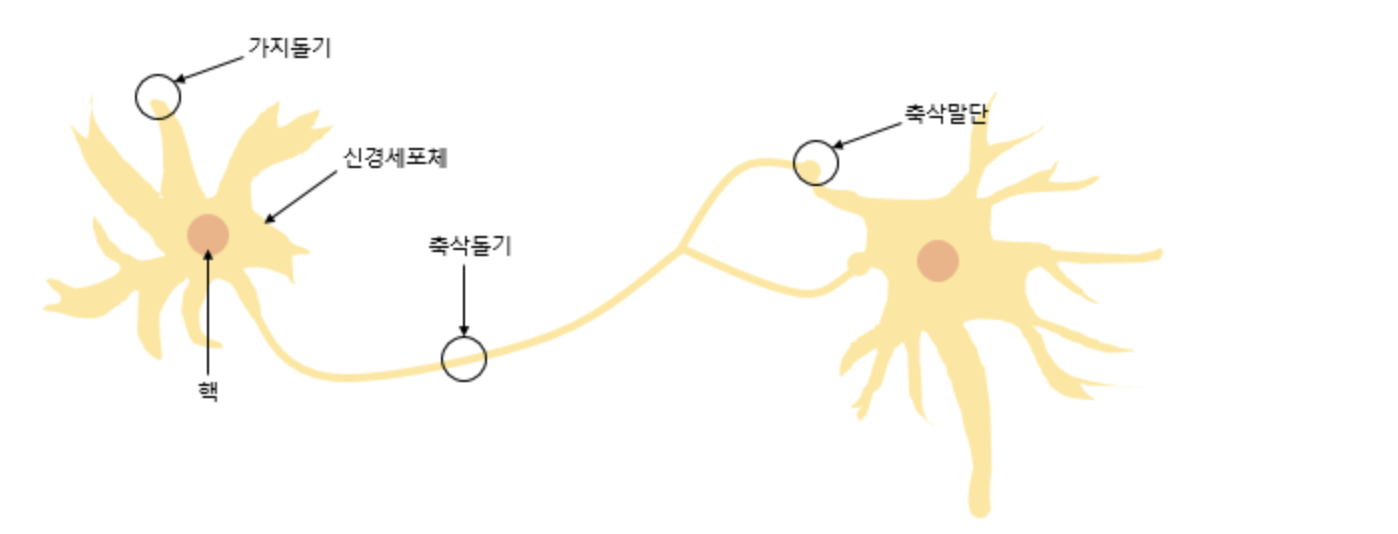
퍼셉트론은 실제 뇌를 구성하는 신경 세포 뉴런의 동작과 유사한데, 신경 세포 뉴런의 그림을 먼저 보도록 하자.

뉴런은 가지돌기에서 신호를 받아들이고, 이 신호가 일정치 이상의 크기를 가지면 축삭돌기를 통해서 신호를 전달한다.

퍼셉트론이란?

퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력한다.

전류가 전선을 타고 흐르는 전자를 내보내듯, 퍼셉트론 신호도 흐름을 만들고 정보를 앞으로 전달한다.

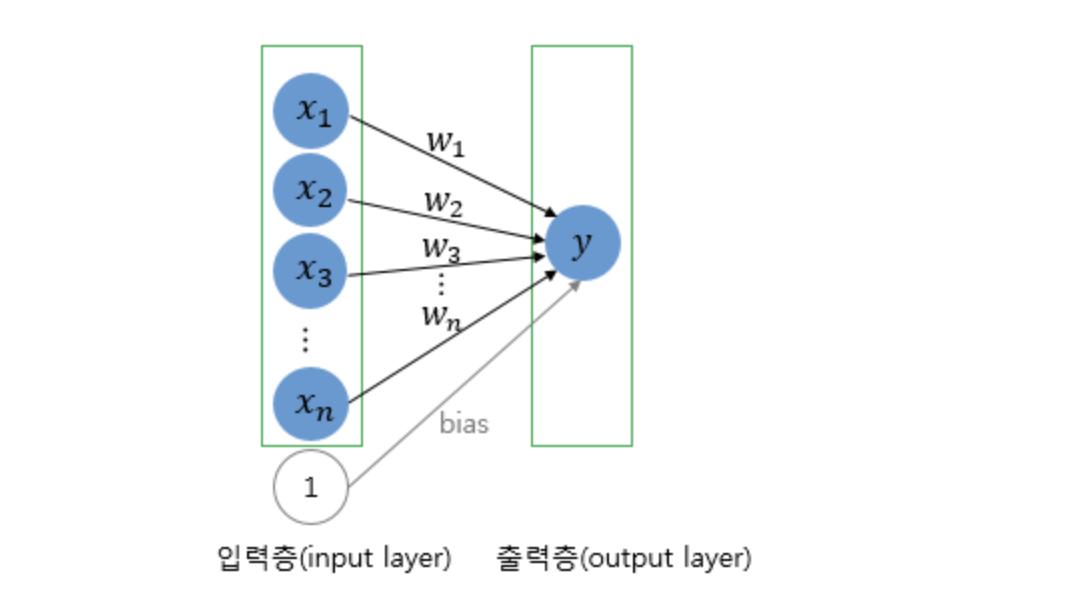
다수의 입력을 받는 퍼셉트론의 그림을 보자. 신경 세포 뉴런의 입력 신호와 출력 신호가 퍼셉트론에서 각각 입력값과 출력값에 해당된다.

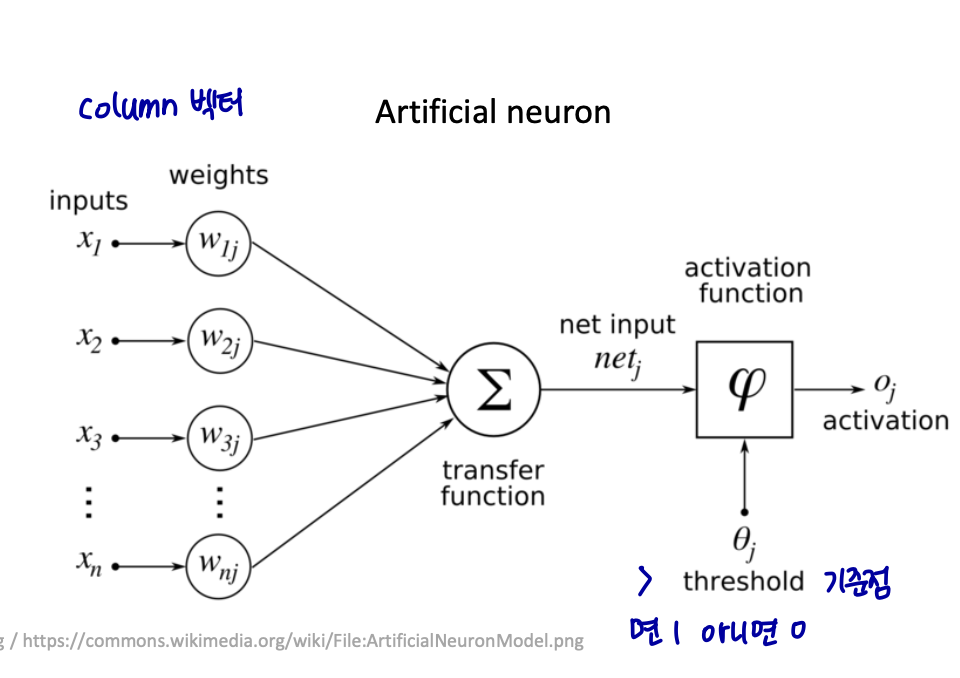
그림은 입력으로 n 개의 input 값을 받은 퍼셉트론이다. x는 입력값을 의미하며, w는 가중치, y는 출력값이다.

실제 신경 세포 뉴런에서의 신호를 전달하는 축삭돌기의 역할을 퍼셉트론에서는 가중치가 대신한다. 각각의 인공 뉴런에서 보내진 입력값 x는 각각의 가중치 w와 함께 종착지인 인공 뉴런에 전달된다.

각각의 입력값에는 각각의 가중치가 존재하는데, 이때 가중치의 값이 크면 클수록 해당 입력 값이 중요하다는 것을 의미한다.

각 입력값이 가중치와 곱해져서 인공 뉴런에 보내지고, 각 입력값과 그에 해당되는 가중치의 곱의 전체 합이 임계치(threshold)를 넘으면 종착지에 있는 인공 뉴런은 출력 신호로서 1을 출력하고, 그렇지 않을 경우에는 0을 출력한다.

이러한 함수를 계단 함수(Step function)라고 하며, 아래는 그래프는 계단 함수의 하나의 예를 보여준다.

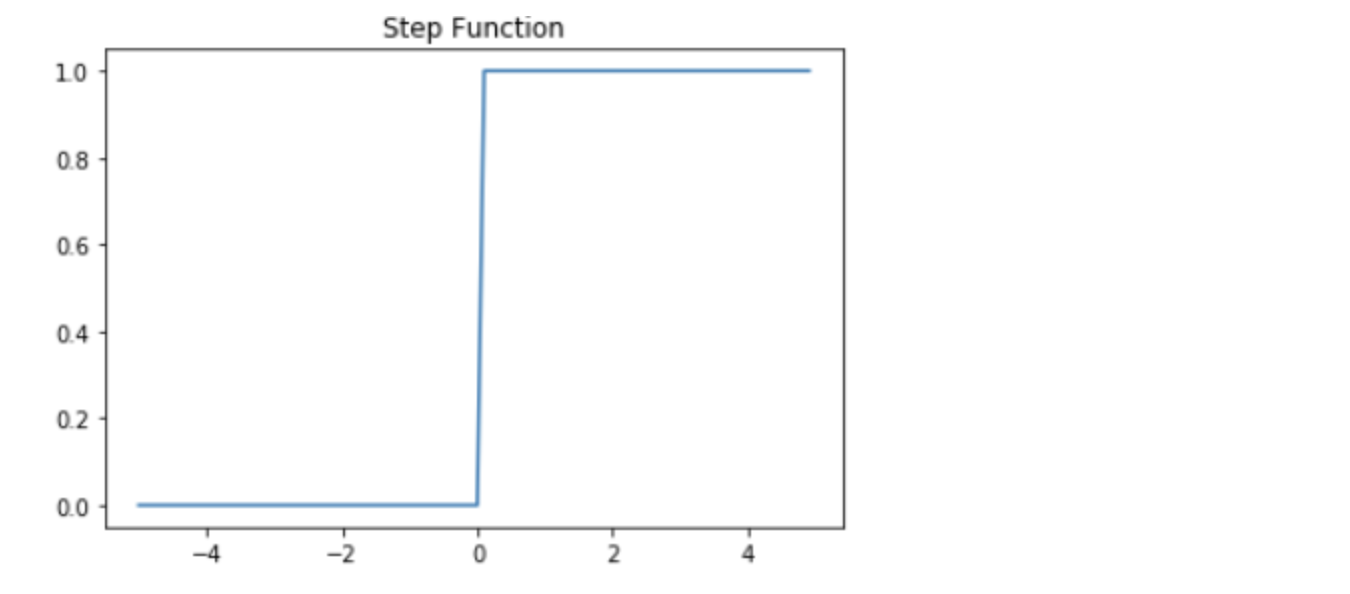
이때 계단 함수에 사용된 이 임계치값을 수식으로 표현할 때는 보통 세타(Θ)로 표현한다.

식으로 표현하면 다음과 같다.

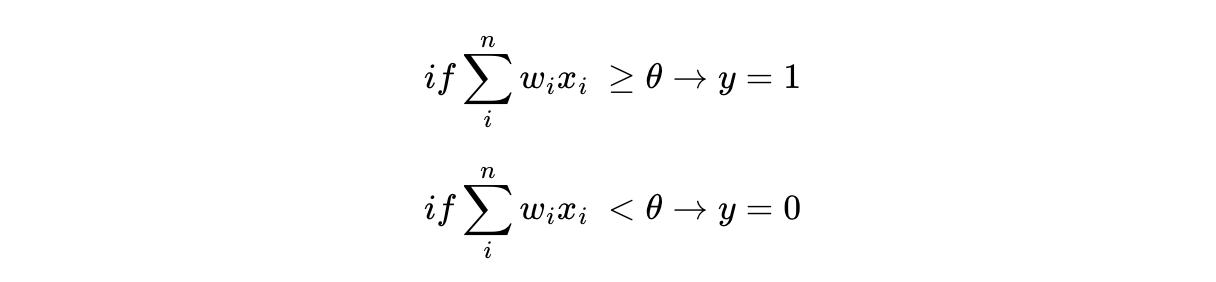
위의 식에서 임계치를 좌변으로 넘기고 편향 b (bias)로 표현할 수도 있다. 편향 b 또한 퍼셉트론의 입력으로 사용된다. 보통 그림으로 표현할 때는 입력값이 1로 고정되고 편향 b가 곱해지는 변수로 표현된다.

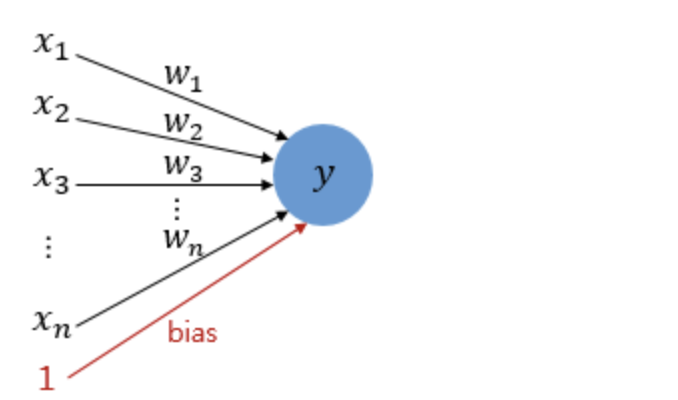
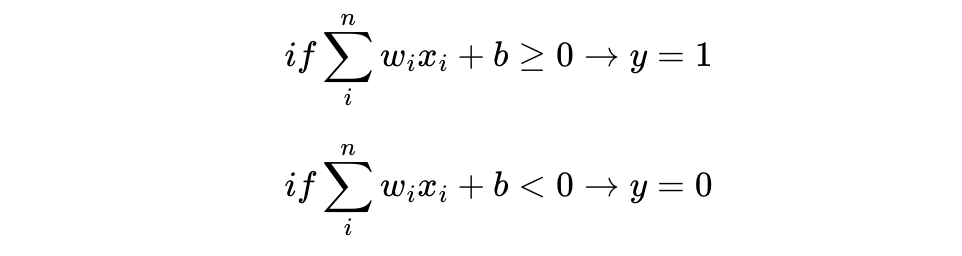
이 책을 포함한 많은 인공 신경망 자료에서 편의상 편향 b가 그림이나 수식에서 생략되서 표현되기도 하지만 실제로는 편향 b 또한 딥 러닝이 최적의 값을 찾아야 할 변수 중 하나이다.

뉴런에서 출력값을 변경시키는 함수를 활성화 함수(Activation Function)라고 한다. 초기 인공 신경망 모델인 퍼셉트론은 활성화 함수로 계단 함수를 사용하였지만, 그 뒤에 등장한 여러가지 발전된 신경망들은 계단 함수 외에도 여러 다양한 활성화 함수를 사용하기 시작했다.

퍼셉트론의 활성화 함수는 계단 함수이지만 여기서 활성화 함수를 시그모이드 함수로 변경하면 퍼셉트론은 곧 이진 분류를 수행하는 로지스틱 회귀와 동일함을 알 수 있다.

다시 말하면 로지스틱 회귀 모델이 인공 신경망에서는 하나의 인공 뉴런으로 볼 수 있다. 로지스틱 회귀를 수행하는 인공 뉴런과 위에서 배운 퍼셉트론의 차이는 오직 활성화 함수의 차이이다.

인공뉴런의 Linear model

• Perceptron

  • step function

  • binary label 예측

  • classification error 최소화

• Linear regression

  • identical function

  • 실수를 예측

  • mean squared error 최소화

• Logistic Regression

  • sigmoid function / logistic function

  • 확률로 binary label 예측

  • cross-entropy error 최소화

단순한 논리 회로

AND 게이트

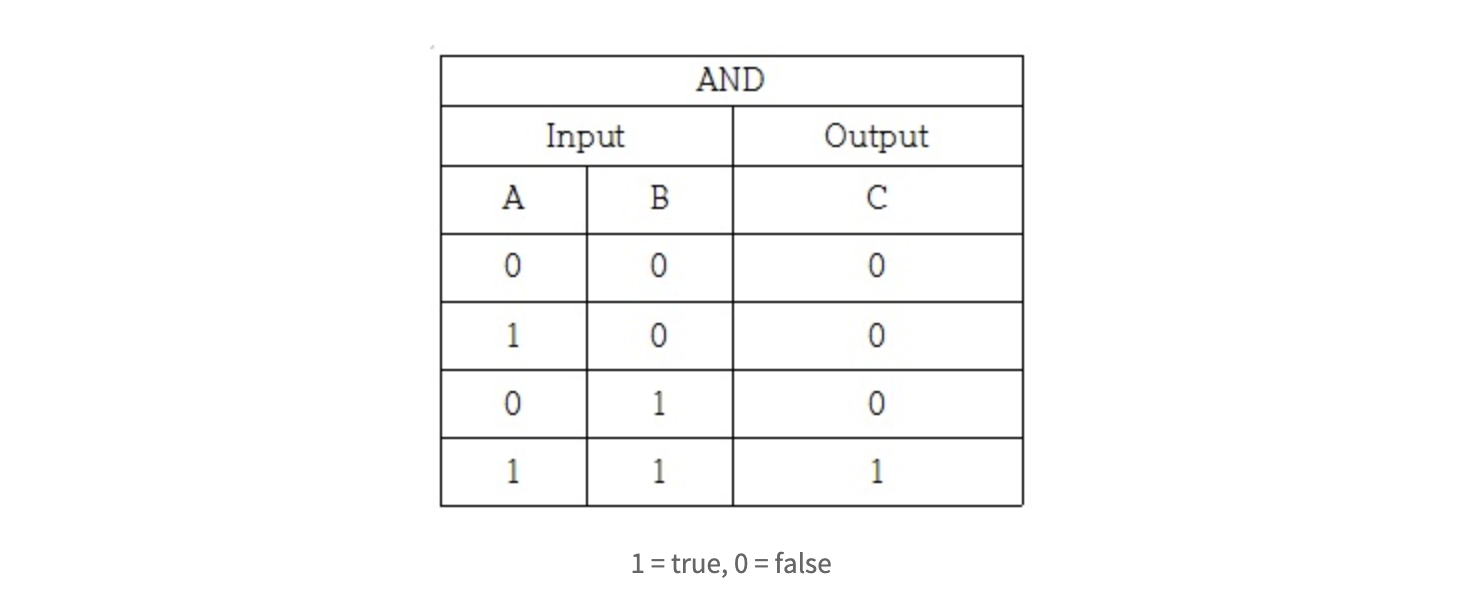
그림과 같은 입력 신호와 출력 신호의 대응 표를 진리표라고 한다.

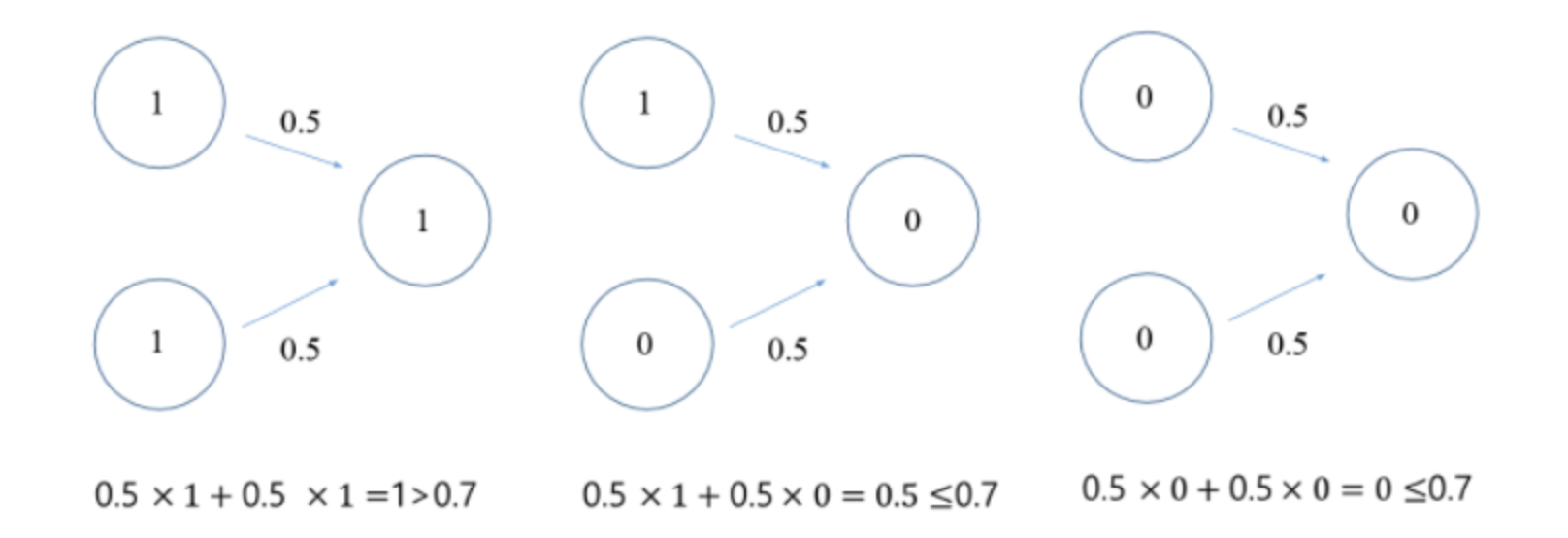
AND 게이트를 퍼셉트론으로 표현하고자 할때 이를 위해 할 일은 그림의 진리표대로 작동하도록 하는 w1, w2, 세타 값을 정하는 것이다.

그럼 어떤 값으로 설정하면 AND 게이트를 충족하는 퍼셉트론을 만들 수 있을까?

답은 매우 여러 개가 나올 수 있다. 현재 공부하는 책에서는 w1, w2: 0.5, 세타(임계점): 0.7로 잡았다.

NAND 게이트

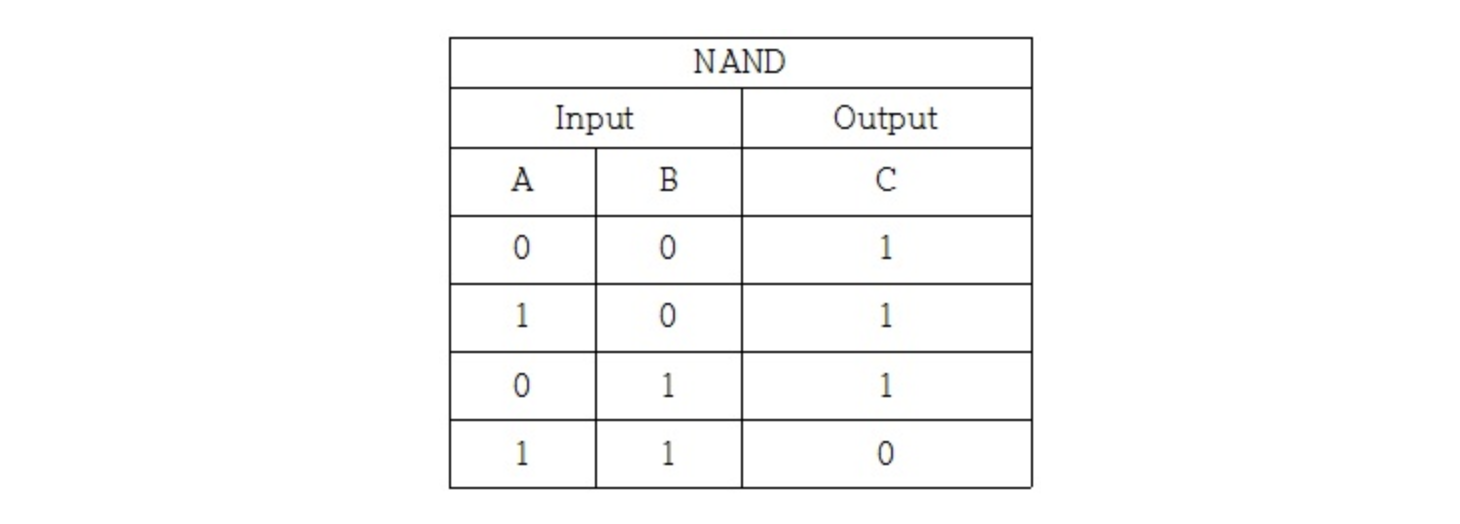
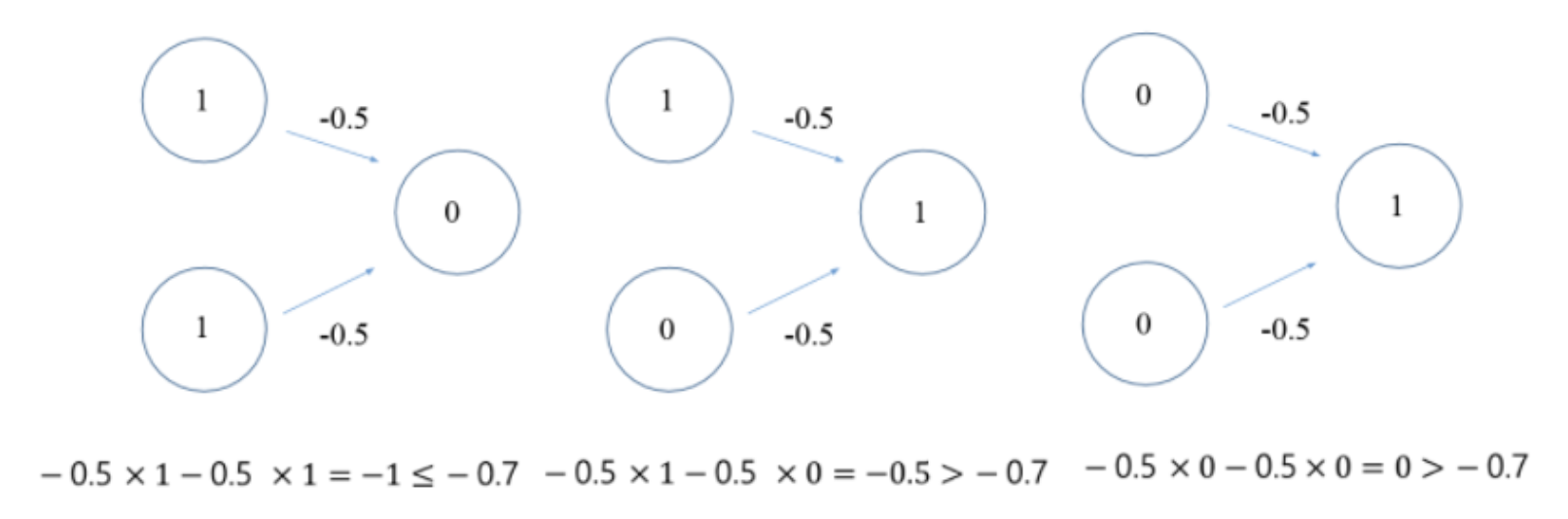
NAND는 Not AND를 의미하여, 그 동작은 AND 게이트의 출력을 뒤집은 것이 된다.

그럼 어떤 값으로 설정하면 NAND 게이트를 충족하는 퍼셉트론을 만들 수 있을까?

책에서는 w1 ,w2 = -0.5, 임계점 = -0.7로 설정했다.

OR 게이트

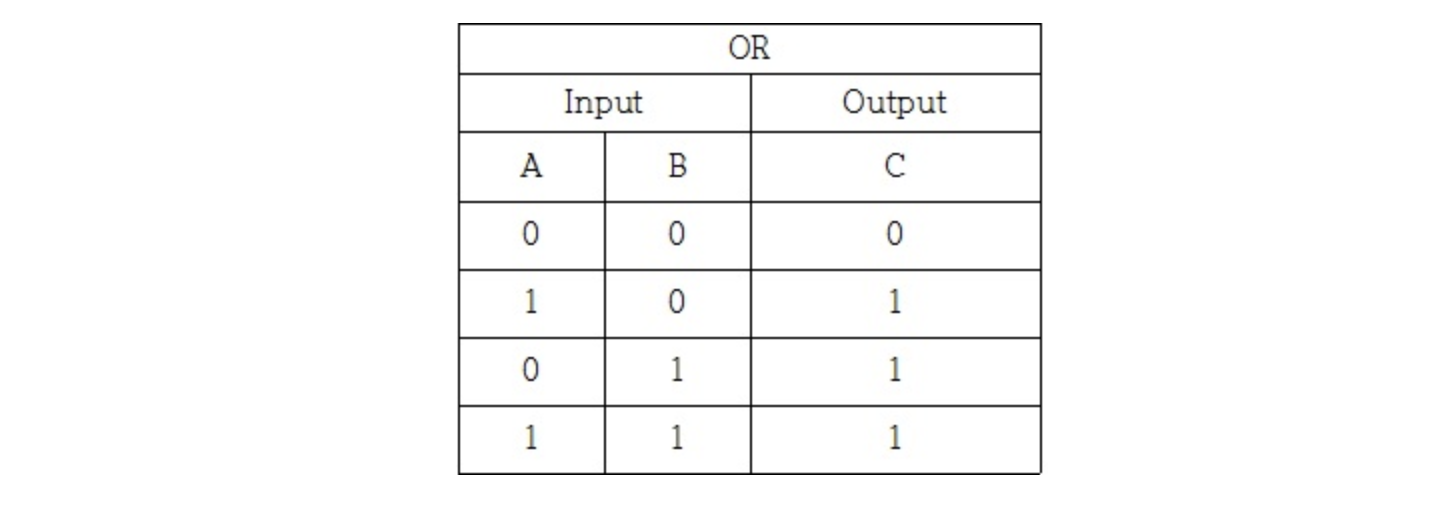
그럼 어떤 값으로 설정하면 OR 게이트를 충족하는 퍼셉트론을 만들 수 있을까?

책에서는 w1, w2 = 0.5, 임계점 = 0.2로 설정했다.

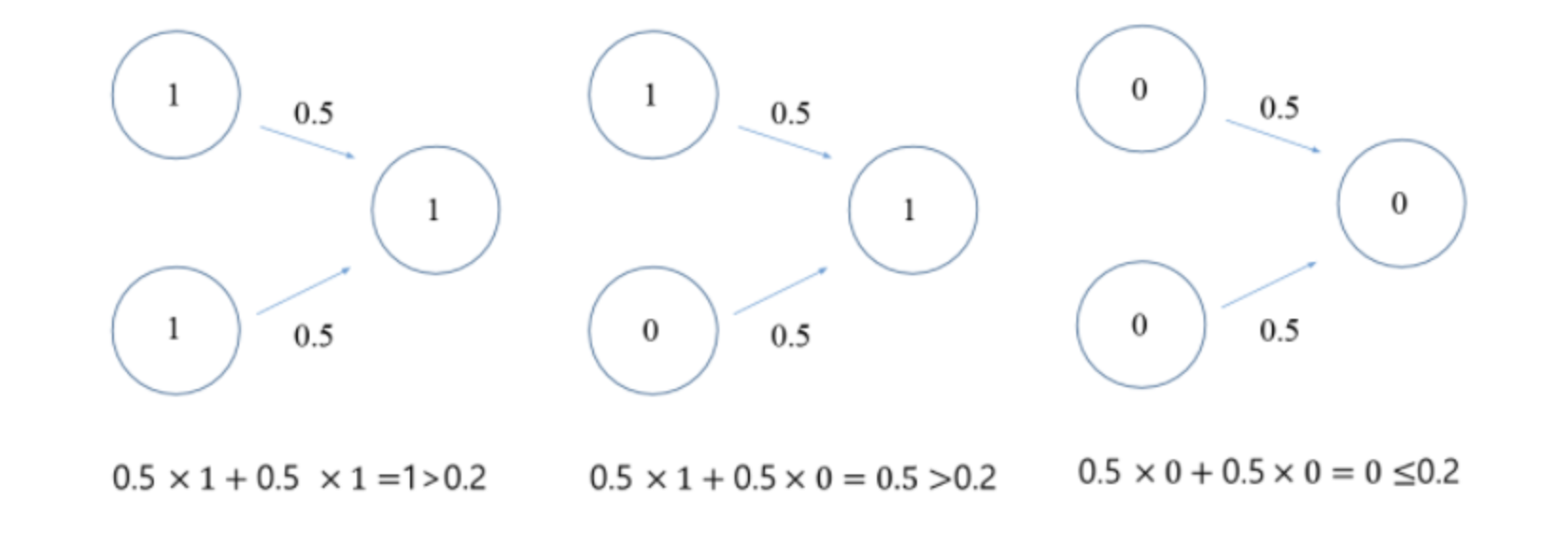
퍼셉트론의 구조는 AND, NAND, OR 게이트에서 모두 똑같다.

퍼셉트론의 한계

XOR 게이트

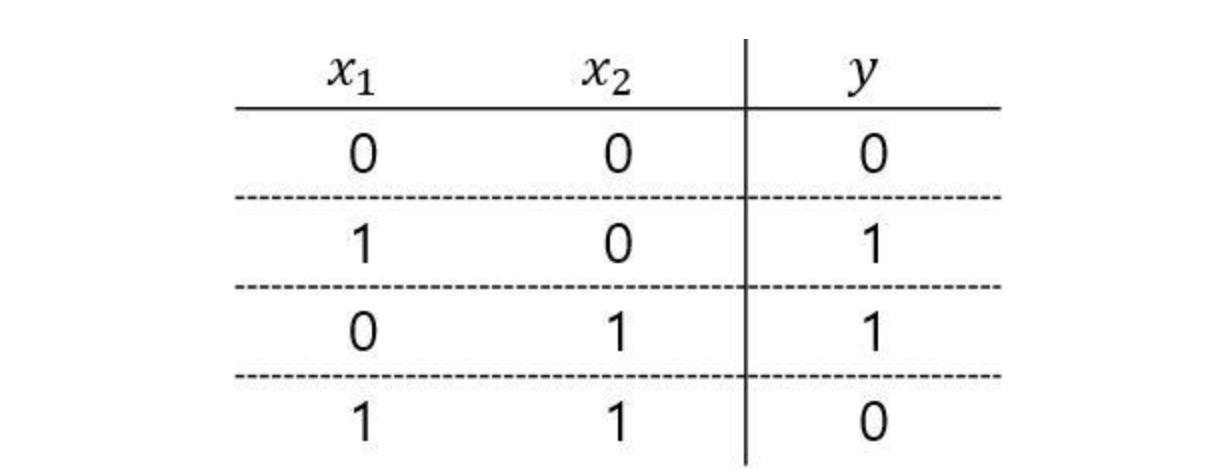
XOR 게이트는 x1과 x2 중 한 쪽이 1일 때만 1을 출력한다.

지금까지 본 퍼셉트론은 XOR 게이트를 구현할 수 없다.

XOR 게이트의 경우 직선 하나로 true, false를 나누는 영역을 만들어 낼 수 없다.

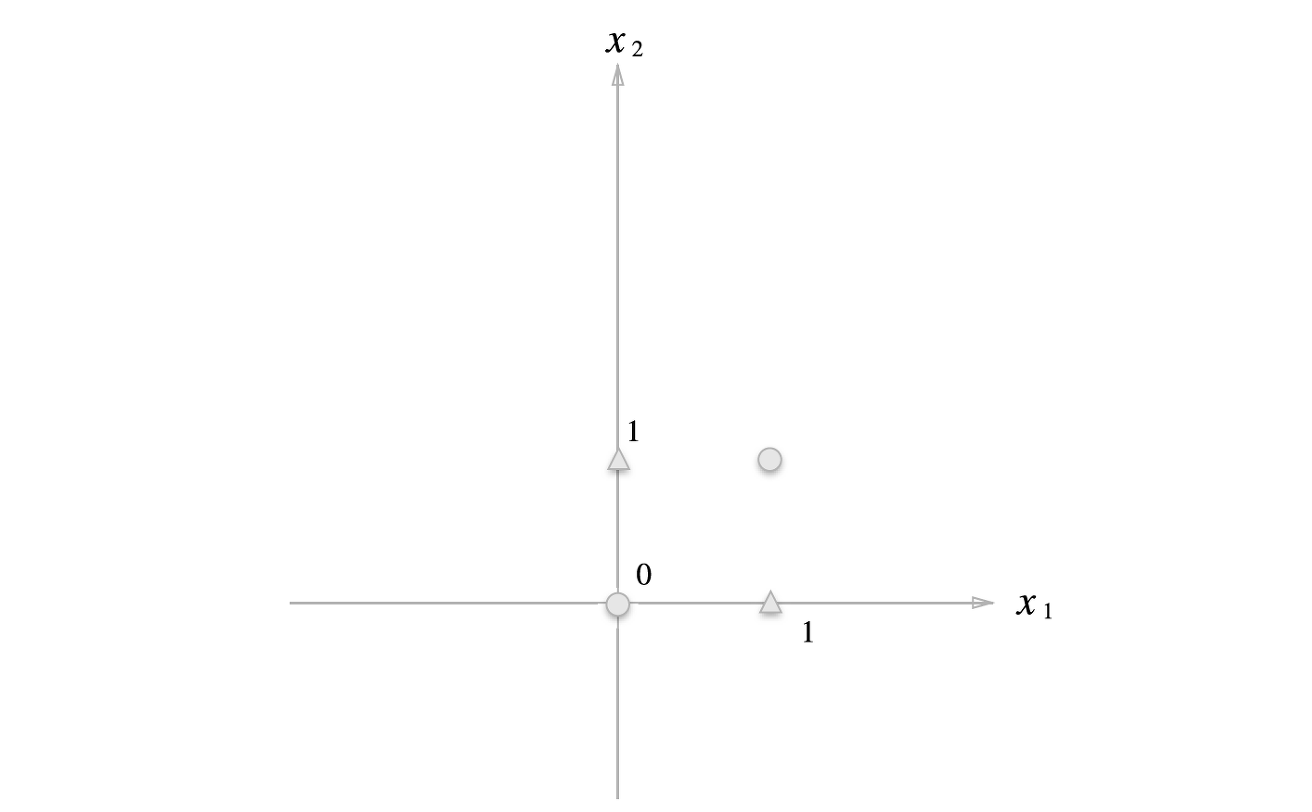
따라서 선형 영역으로는 불가능하고, 곡선으로 나누는 비선형 영역에서는 가능하다.

즉, 단층 퍼셉트론으로는 비선형 영역을 분리할 수 없다.

지금까지 다룬 퍼셉트론을 단층 퍼셉트론이라고 한다.

퍼셉트론은 단층 퍼셉트론, 다층 퍼셉트론으로 나뉘어진다.

단층 퍼셉트론은 값을 보내는 단계와 값을 받아서 출력하는 두 단계로만 이루어진다. 이때, 각 단계를 보통 층(layer)라고 부르며, 이 두 개의 층을 입력층(input layer)과 출력층(output layer)라고 한다.

다층 퍼셉트론 (MultiLayer Perceptron, MLP)

XOR 게이트는 기존의 AND, NAND, OR 게이트를 조합하면 만들 수 있다. 퍼셉트론 관점에서 말하면 층을 더 쌓으면 만들 수 있다. 다층 퍼셉트론과 단층 퍼셉트론의 차이는 단층 퍼셉트론은 입력층과 출력층만 존재하지만, 다층 퍼셉트론은 중간에 층을 더 추가하였다는 점이다.

이렇게 입력층과 출력층 사이에 존재하는 층을 은닉층(hidden layer) 이라고 한다. 즉, 다층 퍼셉트론은 중간에 은닉층이 존재한다는 점이 단층 퍼셉트론과 다르다. 다층 퍼셉트론은 줄여서 MLP라고도 부른다.

즉, XOR 문제나 기타 복잡한 문제를 해결하기 위해서 다층 퍼셉트론은 중간에 수많은 은닉층을 더 추가할 수 있다. 은닉층의 개수는 2개일 수도 있고, 수십 개일수도 있고 사용자가 설정하기 나름이다.

가중치 매개변수의 적절한 값을 데이터로부터 자동으로 학습하는 능력이 이제부터 살펴볼 신경망의 중요한 성질이다.

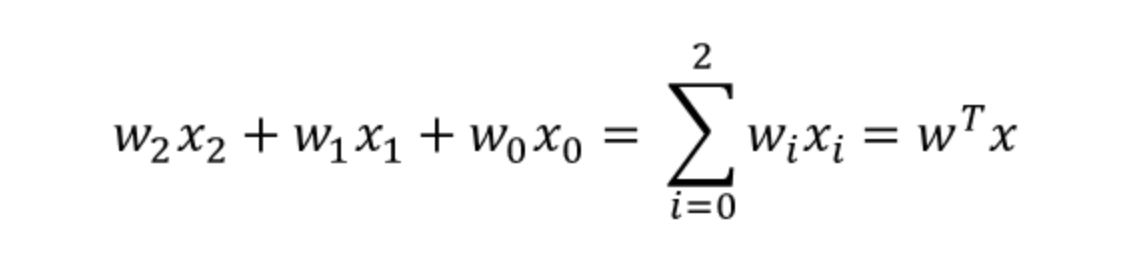
활성화 함수

이처럼 입력값을 출력값으로 변환하는 함수를 활성화 함수라 한다. 말 그대로 활성화 함수는 입력값의 총 합이 활성화를 일으키는지 정하는 역할을 한다.

활성화 함수는 2단계로 처리된다.

• a = b + w1x1 + w2x2
• y = h(a)

입력값에 가중치값을 곱한 값과 편향의 총합을 계산하고 이를 a라 한다. 그리고 a를 함수 h()에 넣어 y값을 출력한다.

Perceptron Learning

목표

• 트레이닝 데이터를 기반으로 최적의 모델 파라메터를 결정하는 것

가정

• data set은 선형적으로 분리가능해야한다.
• 벡터 w는 트레이닝 데이터를 완벽하게 분류한다.

그럼에도 불구하고 misclassification 되는 경우가 발생할 때는 w를 조절하면서 classifier를 수정한다.

Perceptron Learning Algorithm (PLA)

hypothesis를 바꾸는 시기는 주어진 hypothesis가 특정 점을 miclassification 할 때이다. 그러면 loop를 돌면서 이렇게 misclassification이 될 때 weight를 새롭게 업데이트 해준다.

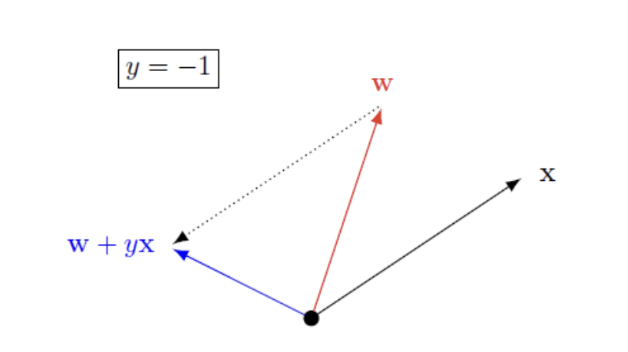
위의 그래프에서 결국 우리가 추구하는 것은 파란색 화살표가 된다.

가장 optimal 한 결과는 모든 요소들이 제대로 분류될 때까지 loop를 도는 것이다. 하지만 만약 주어진 dataset들이 linearly separable하지 않으면 어느 순간 무한루프에 빠지게 된다. 따라서 적절히 분류될때까지만 loop를 돌고 멈춘다.

(threshold 값 이하의 error rate가 나오면 break 되는 형식)