Gradient Descent

본 내용은 공돌이의 수학정리 노트(https://angeloyeo.github.io/2020/08/16/gradient_descent.html) 님의 블로그 정리에 기초합니다.

Gradient Descent

gradient?

• 점 p에서 f의 편미분을 구성 요소로 하는 벡터

• gradient 벡터는 “가장 빠른 증가 방향 및 속도”로 해석할 수 있다.

경사 하강법(Gradient Descent)이란 딥러닝 알고리즘 학습 시 사용되는 최적화 방법 중 하나이다. gradient descent 방법은 1차 미분계수를 이용해 함수의 최소값을 찾아가는 iterative한 방법이다.

경사하강법은 인공 신경망의 출력값과 실제값의 오차가 최소가 되도록 가중치를 결정하는 방법 중 하나이다.

steepest descent 방법은 다음과 같이 많이 비유되기도 한다.

• 앞이 보이지 않는 안개가 낀 산을 내려올 때는 모든 방향으로 산을 더듬어가며 산의 높이가 가장 낮아지는 방향으로 한 발씩 내딛어갈 수 있다.

gradient descent 의 목적과 사용 이유

gradient descent는 함수의 최소값을 찾는 문제에서 활용된다.

함수의 최소, 최댓값을 찾으려면 “미분계수가 0인 지점을 찾으면 되지 않느냐?”라고 물을 수 있는데, 미분계수가 0인 지점을 찾는 방식이 아닌 gradient descent를 이용해 함수의 최소값을 찾는 주된 이유는

• 우리가 주로 실제 분석에서 맞딱드리게 되는 함수들은 닫힌 형태(closed form)가 아니거나 함수의 형태가 복잡해 (가령, 비선형함수) 미분계수와 그 근을 계산하기 어려운 경우가 많고,

• 실제 미분계수를 계산하는 과정을 컴퓨터로 구현하는 것에 비해 gradient descent는 컴퓨터로 비교적 쉽게 구현할 수 있기 때문이다.

추가적으로,

• 데이터 양이 매우 큰 경우 gradient descent와 같은 iterative한 방법을 통해 해를 구하면 계산량 측면에서 더 효율적으로 해를 구할 수 있다.

gradient descent의 수식 유도

gradient descent는 함수의 기울기(즉, gradient)를 이용해 x의 값을 어디로 옮겼을 때 함수가 최소값을 찾는지 알아보는 방법이라고 할 수 있다.

기울기가 양수라는 것은 x값이 커질 수록 함수 값이 커진다는 것을 의미하고, 반대로 기울기가 음수라면 x값이 커질 수록 함수의 값이 작아진다는 것을 의미한다고 볼 수 있다.

또, 기울기의 값이 크다는 것은 가파르다는 것을 의미하기도 하지만, 또 한편으로는 x의 위치가 최소값/최댓값에 해당되는 x 좌표로부터 멀리 떨어져있는 것을 의미하기도 한다.

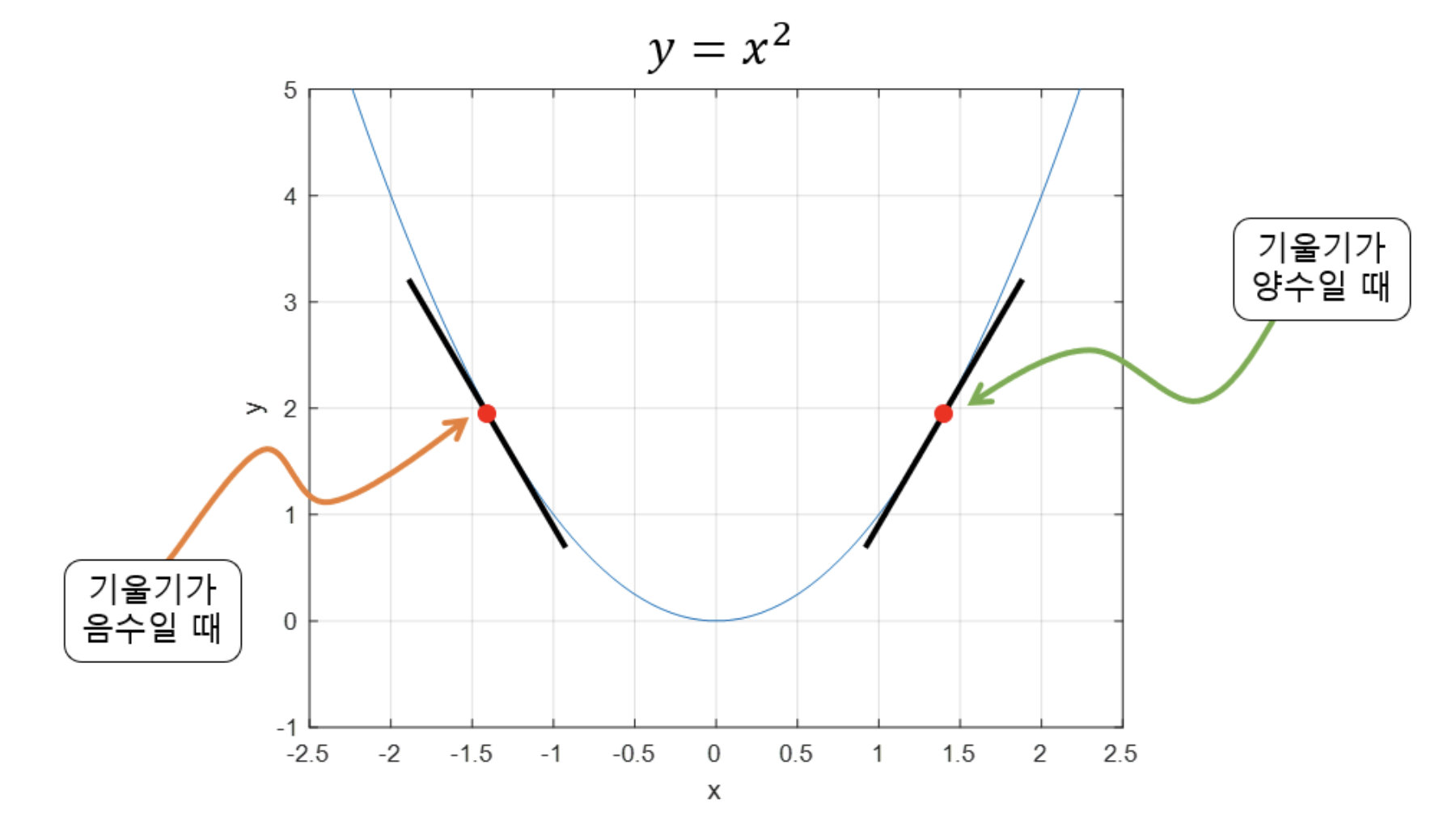
gradient의 수식

이를 이용해 특정 포인트 x에서 x가 커질 수록 함수값이 커지는 중이라면 (즉, 기울기의 부호는 양수) 음의 방향으로 x를 옮겨야 할 것이고,

반대로 특정 포인트 x에서 x가 커질 수록 함수값이 작아지는 중이라면 (즉, 기울기의 부호는 음수) 양의 방향으로 x를 옮기면 된다.

이 논리를 수식으로 쓰면 다음과 같다.

xi+1 = xi − 이동 거리 × 기울기의 부호

그러면 여기서 이동거리는 어떻게 생각해야 할까? 그것은 gradient의 크기를 이용하면 된다.

gradient의 크기

이동거리는 어떻게 구할지 생각해보아야 한다.

이 문제에 대해 다시 잘 생각해보면 미분 계수(즉, 기울기 혹은 gradient)값은 극소값에 가까울 수록 그 값이 작아진다.

사실 극대값에 가까울 때에도 미분 계수는 작아지기 마련인데, gradient descent 과정에서 극대값에 머물러 있는 경우는 극히 드물기 때문에 이 문제에 대해서는 고려하지 않고자 한다.

따라서, 이동거리에 사용할 값을 gradient의 크기와 비례하는 factor를 이용하면 현재 x의 값이 극소값에서 멀 때는 많이 이동하고, 극소값에 가까워졌을 때는 조금씩 이동할 수 있게 된다.

즉, 이동거리 는 gradient 값을 직접 이용하되, 이동 거리를 적절히 사용자가 조절 할 수 있게 수식을 조정해 줌으로써 상황에 맞게 이동거리를 맞춰나갈 수 있게 하면 될 것이다.

xi+1 = xi − α∇f(xi)

α: learning rate

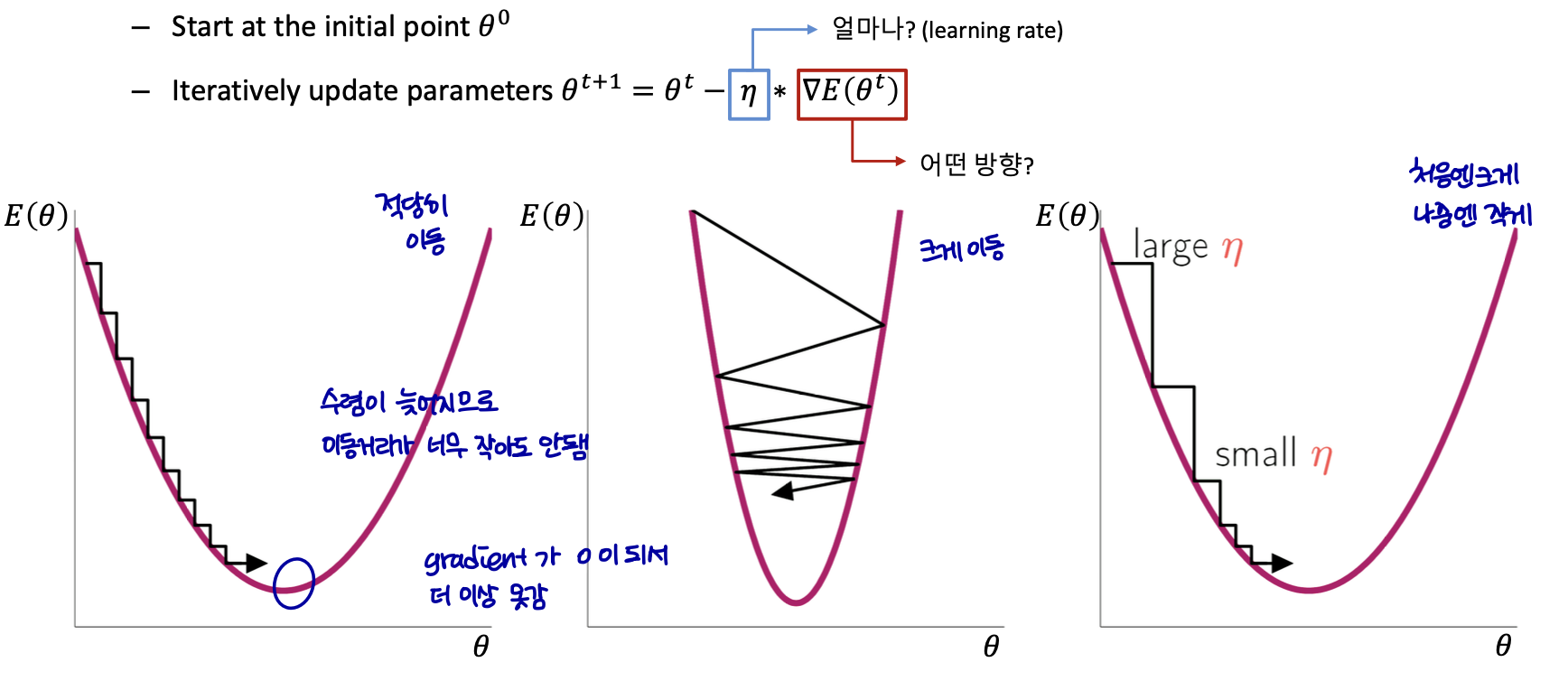
step size가 큰 경우 한 번 이동하는 거리가 커지므로 빠르게 수렴할 수 있다. 하지만 step size를 너무 크게 설정해버리면 최소값을 계산하도록 수렴하지 못하고 함수 값이 계속 커지는 방향으로 최적화가 진행될 수 있다.

또한, step size가 너무 작은 경우 발산하지는 않을 수 있지만 최적의 x를 구하는데 소요되는 시간이 오래 걸린다는 단점이 있다.

Gradient Descent

Local Minimum 문제

경사 하강법은 볼록 함수의 경우 gradient descent를 이용해 극소를 무조건 찾을 수 있다.

하지만, 경사 하강법은 비볼록 함수의 경우, 파라미터의 초기 시작 위치에 따라 최적의 값이 달라진다는 한계가 있다. 일반적인 경우 non-convex 함수인 경우가 많고, 성능이 더 좋기 때문에 non-convex 함수를 많이 사용한다.