📝 이번 포스트는 "MixMatch: A Holistic Approach to Semi-Supervised Learning"논문에 대해 알아보는 시간을 갖도록 하겠습니다.
Abstact
이 논문의 전반적인 내용을 압축해서 설명하는데요,
연구팀은 당시 현존하는 semi-supervised learning 기법을 통합하여 새로운 알고리즘인 MixMatch를 개발했다고 합니다.
MixMatch는 데이터 증강된 unlabeled example들에 대한 낮은 Entropy 레이블을 추측하고, labeled 데이터와 unlabeled 데이터를 섞는 MixUp이라는 방법을 사용합니다.
MixMatch는 CIFAR-10 데이터셋에서 error rate를 4배 줄였고(38% -> 11%) STL-10 데이터셋에서 error rate를 2배 줄였다고 합니다.
1. Introduction
최근 많은 연구들이 준지도학습에 unlabel 데이터에손실함수를 계산하고 보지 못했던 데이터에 대해 일반화하는 것을 추구하는 경향이 있습니다.
최근 많은 연구에서 아래 3개 중 하나에 대한 손실 함수를 다룹니다.
- entropy minimization : 모델이 unlabel 데이터에 대한 prediction 결과를 confident하게 합니다.
- consistency regularization : 모델의 입력 데이터가 동일하지 못할 때 output distribution을 최대한 같게 하도록 합니다.
- generic regularization : 모델이 일반화가 잘 되게 하고, 학습 데이터셋에 과적합 되는 것을 방지하게 합니다.
저자는 MixMatch를 위의 세 가지 손실 함수를 통합하여 하나의 손실 함수로 구현한 준지도학습(SSL)이라고 소개합니다.
이전 방법론들과 다르게 MixMatch는 뒤따르는 이점을 갖습니다.
- 표준 이미지 벤치마크에 대해서 SOTA급의 결과를 도출하였다. CIFAR-10에서는 에러율을 4배 줄였습니다.
- MixMatch가 각 부분의 합??(논문 뒷부분에 자세하게 설명된다)보다 크다는 것을 ablation 연구에서 알 수 있었습니다.
- Mixmatch는 차별적인 개인 학습에 유용하다는 것을 증명했고, PATE 프레임워크?? student들이 새로운 SOTA급 결과를 얻을 수 있게 했다.(뒤에서 자세하게 설명)
간략하게 요약해보자면 MixMatch는 unlabel 데이터에 대한 entropy를 줄이는 동시에 기존의 정규화 기술과 compatible하게 하는 손실함수들을 하나로 통합했습니다.
2. Related Work
연구팀이 MixMatch를 연구할 때 주로 참고하였던 것들에 대해 설명합니다.
자세한 것은 아래 2.1, 2.2, 2.3으로 나누어 설명합니다.
2.1 Consistency Regularization
지도학습에서 일반적인 regularization 기법은 데이터 증강 기법이다.
데이터 증강 기법은 클래스에는 영향을 미치면 안되는 것을 가정이 되어야 합니다.
예를 들어 이미지 분류 작업에서 data augmentation을 할 때 이미지가 확대되거나, 축소한다거나, 혹은 노이즈를 넣어주는 등의 작업은 픽셀에 대해서만 영향을 줘야하고, label이 변경이 되면 안됩니다.
즉, consistency regularization은 클래스 분포가 augmentation하기 전 unlabel 데이터의 class distribution이나 augmentation 후의 class distribution이 일관되야 한다는 것입니다.
Consistency Regularization 공식은 위와 같이 L2 loss입니다.
2개의 항이 똑같아보이지만, Mean Teacher가 하나의 항을 대체합니다.
모델의 output이 지수이동평균(Exponential Moving Average)을 이용한 값이 됩니다.
위 항 중 아무거나 대체되어도 두 항의 차이의 제곱이 계산되기때문에 앞 항이 대체되거나 뒷 항이 대체되어도 상관이 없습니다.
하지만 이 방법의 단점은 특정 도메인의 데이터 증강기법을 사용한다는 것이다.
2.2 Entropy Minimization
준지도학습의 일반적으로 기본적인 가정은 분류작업의 decision boundary가 고밀도 지역을 통과해서는 안된다는 것입니다.
이것을 실현하기 위해서는 classifier가 unlabel 데이터에 대한 low-entropy한 prediction을 결과로 도출해야합니다.
unlabel 데이터 에 대한 의 엔트로피를 최소화 하는 손실 항으로 합니다.
"Pseudo-Label" 알고리즘은은 암묵적으로 unlabel 데이터에 대한 high-confidence prediction를 hard label(=one hot label)로 구성하고 이것을 training 시에 사용합니다.
MixMatch 역시 비슷한 방법인 unlabel 데이터에 대한 클래스 분포를 "sharpening"기법을 통하여 entropy minimization을 수행합니다.
2.3 Traditional Regularization
Regularization은 모델에 제약을 걸어서 training 데이터를 기억하기 어렵게 하여 학습 시에 학습 시에 사용하지 않은 데이터를 일반화할 수 있도록 합니다.
즉 training data에 overfitting 되는 것을 방지하는데 도움을 주고 학습 시에 사용되지 않은 데이터를 일반화할 수 있도록 해줍니다.
저자는 모델 파라미터에 L2 norm에 패널티를 부과하는 weight decay를 사용합니다.
그리고 MixMatch는 MixUp 방법을 label 데이터와 unlabel 데이터 모두에게 사용하였습니다.
MixUp에 대해서는 뒤에서 자세하게 설명하겠습니다.
3. MixMatch
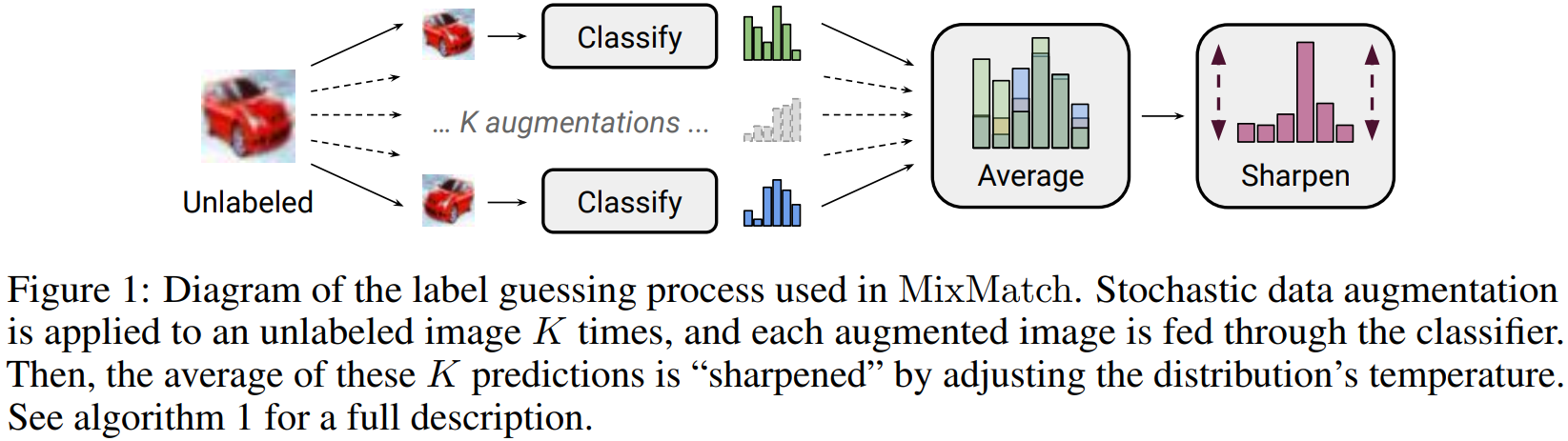
이 파트에서 MixMatch에 대해 자세하게 설명합니다.
MixMatch는 표현하자면 전체론적으로 준지도학습 분야에서 지배적인 패러다임에서 아이디어와 요소들을 구성하는 방법론입니다.
MixMatch 알고리즘의 전반적인 구조는 뒤에서 자세하게 다룰 것입니다.
figure 1은 unlabel 데이터에 대해 label을 guessing한 결고과를 평균내과 최종적으로 sharpening하는 과정을 그린 것입니다.

3.1 Data Augmentation
이제 위 Algorithm 1을 보면서 MixMatch 알고리즘을 자세하게 분석해보겠습니다.
MixMatch 방법론은 다른 전형적인 준지도학습 방법론들과 유사하게 label 데이터와 unlabel 데이터 둘 다 augmentation을 합니다.
Stochastic data augmentation을 사용했다고 하는데, 종류는 Flip, Rotate, Crop andResize, Histogram equalization, Adding noise가 있습니다.
위 알고리즘에 나오는 용어들을 짚고 넘어가면서 설명하겠습니다. 와 등 몇가지 변수들은 위에서도 언급을 했지만 다시 한번 설명 드리자면
- : 원 핫 인코딩된 label 데이터의 batch
- : unlabel 데이터 batch
- : 로부터 증강된 label 데이터의 batch
- : 로부터 증강된 unlabel 데이터의 batch
- : 배치 사이즈
- : 배치 내의 데이터 인덱스(= 반복문을 수행할 때 해당 인덱스)
- : MixMatch의 Sharpening에 사용될 Temperature parameter
- : MixMatch의 레이블에 대한 data augmentation 횟수
- : distribution parameter for MixUp
입니다.
위 Algorithm 1에서 Data Augmentation 파트만 보자면 아래 pseudo code와 같습니다.

line 2를 보시면 배치 사이즈 만큼 반복 횟수를 갖고 반복을 진행합니다.
다음 line 3를 보면 b번째 label 데이터 에 대해 augmentation한 데이터를 로 표현합니다.
긜고 line 4, 5를 보면 unlabel 데이터에 대해 증강할 횟수 만큼 반복하면서 b번째 unlabel 데이터 에 대해서 augmentation을 적용한 unlabeled 데이터를 를 말합니다.
여기서 알아야 할 점은 label 데이터 의 증강횟수는 1번이고 unlabel 데이터 의 증강횟수는 번이라는 점입니다.
방금 설명드렸던 Stochastic data augmentation 중에서 랜덤하게 K번 증강하는 것입니다.
는 와 같이 one-hot encoding된 레이블을 갖을 것입니다.
하지만는 다르죠. 이 문제가 MixMatch가 풀어나가고자 하는 이유입니다.
3.2 Label Guessing
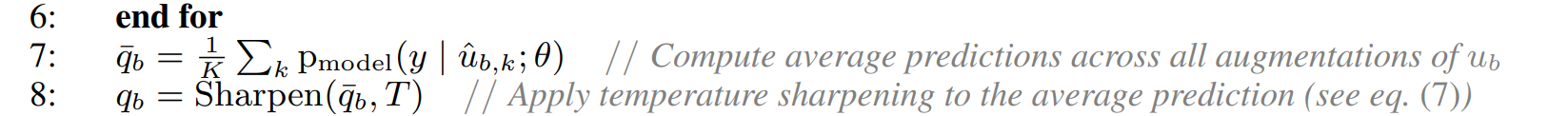
그 다음으로 unlabel 데이터에 대해 모델을 prediction을 하여 "guess"를 만들어냅니다.
"guess"라 하면 test 단계에서 prediction하여 나온 class distribution 결과를 말합니다.
@@@이 "guess"는 뒤에서 unsupervised loss 항에서 사용됩니다.
모든 에서부터 증강되어 파생된 들(, ... )들의 모델이 예측한 class distribution들을 평균을 구한 것을 라고 합니다.
line 7에 구현되어있죠.
이 부분이 consistency regularization을 뜻합니다. 위에서 entropy minimization, consistency regularization, generic regularization을 통합하여 하나의 손실함수로 구현했다고 하였는데 이 부분이 consistency regularization 파트에 해당합니다. 왜냐하면 각 증강된 데이터들의 평균을 구하여 일관성이 유지되기 때문입니다.
sharpening
Label Guessing 단계에서 추가적인 단계인 sharpening 기법을 거칩니다.
왜냐하면 augmentation을 거친 데이터들의 평균인 가 주어졌을 때, sharpening 기법을 적용시켜 class distribution에 대한 entropy를 줄이려고 사용합니다.
sharpening 기법에 Temperature라는 변수 가 수식에 구현이 되는데 어떻게 구현되냐면
로 구현됩니다. Softmax와 유사하게 생겼죠. 실제로 Softmax와 목적이 똑같습니다.
class distribution을 더 뚜렷하게 하기 위한 목적입니다.
T는 0에 가까울수록 class distribution이 뚜렷해질 것입니다.
뚜렷해지는 이유를 한 번 예를 들어 설명해보겠습니다.
만약 T = 0.1이고 그리고 모델의 prediction 결과가 = [0.1, 0.8, 0.07, 0.03]라고 가정해봅시다.
만약 이렇게 구성된다면 겠죠.
일 겁니다.
이들의 합 분의 각 요소를 표현해보면 되게 뚜렷해집니다.
- sharpening을 적용 전 : [0.1, 0.8, 0.07, 0.03]
- sharpening을 적용 후 : [0.0152, 0.9759, 0.0075, 0.0014]
로 되게 뚜렷해지는게 one-hot encoding에 가까운 형태를 갖게 되죠. 논문에서는 이것을 "Dirac distribution"에 가까워진다고 하는데 이 용어는 물리전자 분야에서 사용되는 용어인데 one-hot encoding과 유사한 말입니다.
어쨋든 이렇게 되면 entropy를 낮출 수도 있게 됩니다.
만약 의 범위를 이 아닌 의 범위를 갖는다면 어떻게 될까?
이라고 가정해보자, 그렇다면 = [0.1, 0.8, 0.07, 0.03] 가 주어졌을 때
- sharpening을 적용 전 : [0.1, 0.8, 0.07, 0.03]
- sharpening을 적용 후 : [0.2449, 0.3016, 0.2364, 0.2172]
로 오히려 각 요소들이 값이 골고루 분산된 형태를 갖게 된다.
이것은 sharpening이 아니다.
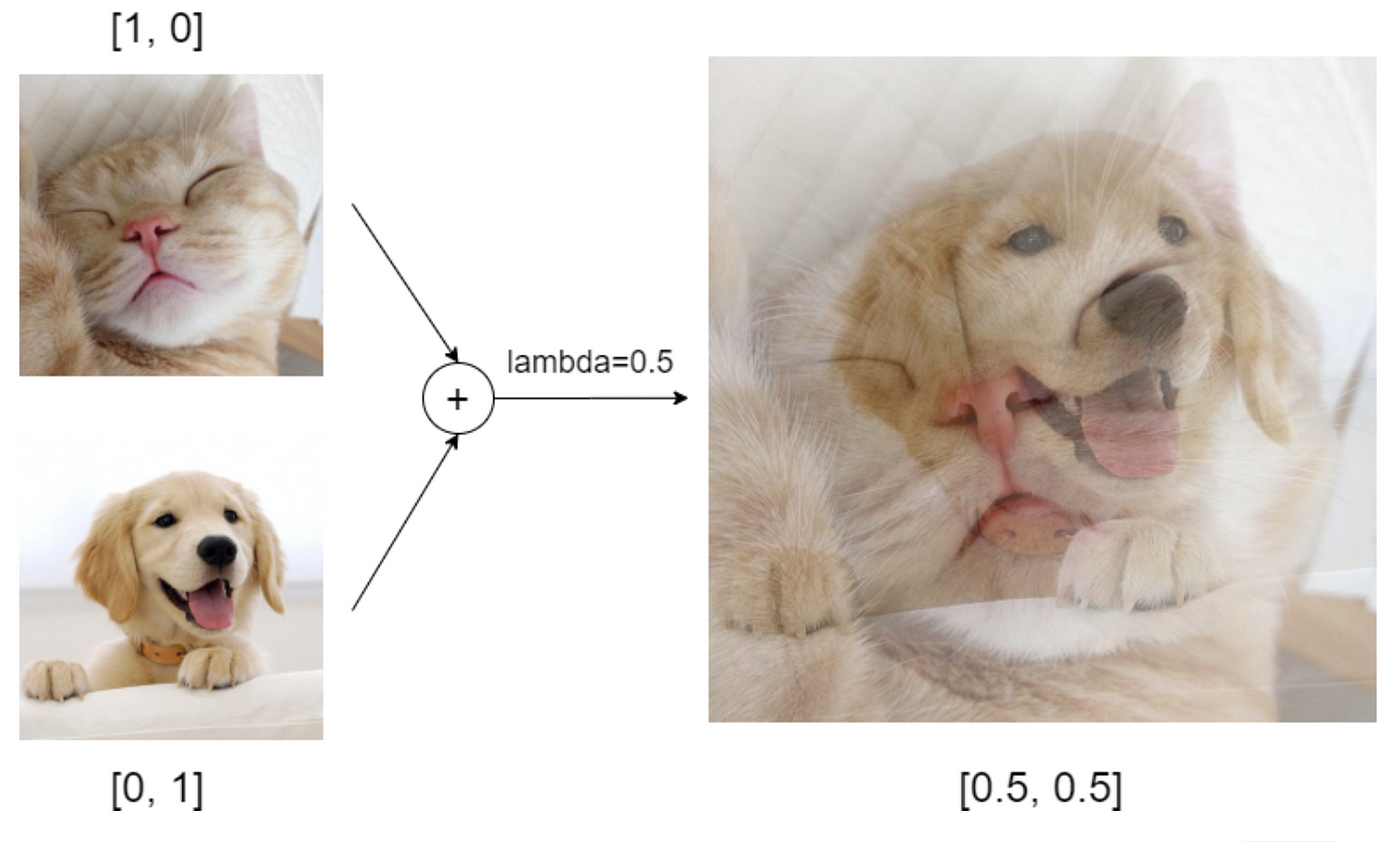
3.3 MixUp
MixUp이란?
MixUp은 두 개의 학습 데이터를 혼합하여 새로운 데이터를 만들어내는 알고리즘을 말합니다.
이미지에 대해서는 라는 변수를 사용하여는 원본 이미지를 말하고 는 두 이미지로부터 새롭게 생성된 이미지를 말합니다.
레이블 또한 같은 방식으로 새로운 레이블 를 생성합니다.
비교적 간단한 알고리즘이지만 주요한 데이터 증강 기법 중 하나로 자리매김하였습니다.
연구팀은 이전 MixUp과 다르게 label 데이터와 unlabel 데이터를 혼합합니다.
이 unlabel 데이터는 "Guess"를 한 class distribution을 갖습니다.
위 식은 MixUp 과정을 표현한 것입니다.
2번째 식에서 와 중 최댓값을 구하는 이유는 3번째 식과 4번째 식에서 과 에게 더 큰 비중을 부여하여 새로운 데이터를 생성하기 위한 저자의 의도입니다.

그 다음 label 데이터로부터 augmentation된 데이터 배치인 과 unlabel 데이터로부터 augmentation된 데이터 배치인 을 이용하여(line 10, 11 참고),
와 를 결합하고 섞습니다. 섞은 데이터들을 에 저장합니다. (line 12 참고)
의 크기는 개의 순서가 뒤섞인 데이터 집합이 될 것입니다.
그 다음으로 이제 MixUP을 진행합니다.
label 데이터로부터 augmentation된 데이터 와 뒤섞인 가 MixUp 과정을 거치는데, 의 크기와 의 크기가 동일하지 않다는 것을 알아야 합니다.
왜냐하면 는 개의 데이터를 갖지만 는 개의 데이터를 갖기 때문에 동일한 크기의 반복문 아래에서 모든 데이터가 MixUp될 수 없다는 것입니다.
가 개만 사용되어 MixUp을 수행하고 에 저장됩니다. (line 13 참고)
나머지 개는 와 MixUp을 수행할 수 없습니다.
남은 개의 는 과 MixUp이 되어 에 저장됩니다. (line 14 참고)
3.4 Loss Function
이 부분에서는 손실함수에 대해 설명합니다.
one-hot encoding된 배치 단위의 label 데이터 와 와 같은 사이즈의 배치 단위의 unlabel 데이터 가 주어졌을 때, MixMatch를 통해 를 증강한 배치 단위의 label 데이터 와 를 증강한 배치 단위의 unlabel 데이터 을 만들어냅니다.
- : 원 핫 인코딩된 label 데이터의 batch
- : unlabel 데이터 batch
- : 로부터 증강된 label 데이터의 batch
- : 로부터 증강된 unlabel 데이터의 batch
- : MixMatch의 Sharpening에 사용될 Temperature parameter
- : MixMatch의 레이블에 대한 data augmentation 횟수
- : distribution parameter for MixUp
그 다음, label 데이터에 대한 손실함수 와 unlabel 데이터에 대한 손실함수를 개별적으로 계산합니다.
아래 공식은 label 데이터에 대한 손실함수 에 대한 손실함수 수식입니다.
- : label 데이터에 대한 손실 함수
- : label 데이터
- : 모델의 prediction
- : 모델의 parameter
- : 모델이 예측한 class distribution
- : one-hot encoding된 레이블
- : 정답인 one-hot encoded label과 모델이 예측한 prediction한 class distribution 사이의 Cross Entropy
아래 공식은 unlabel 데이터에 대한 손실함수 에 대한 손실함수 수식입니다.
- : unlabel 데이터에 대한 손실 함수
- : 클래스의 개수
- : unlabel 데이터
- : unlabel 데이터에 대한 prediction된 class distribution
label 데이터에 대한 손실함수 와 unlabel 데이터에 대한 손실함수 상대적인 비율로 더하여 손실함수 을 구합니다..
- : label 데이터의 손실함수와 unlabel 데이터의 손실함수를 결합한 손실함수
- : label 데이터에 대한 손실함수와 unlabel 데이터에 대한 손실함수 비중을 고려하는 하이퍼 파라미터
Hyperparameters
여태까지 언급되었던 하이퍼파라미터들을 얘기합니다.
특히 unlabel 데이터의 학습 때 (sharpening temperature), (unlabel 데이터의 augmentation 횟수) MixUp 때 사용되는 , 손실함수를 구할 때 label 데이터에 대한 손실함수와 unlabel 데이터에 대한 손실함수 비중을 고려하던 가 사용되었죠.
연구팀은 , 로 설정하고 실험을 진행했다고 합니다.
와 만 데이터셋 별로 다르게 설정했다고 합니다.
실증적으로 얻은 최적의 초기값은 와 이 가장 튜닝하기 적절한 최적의 초깃값이라고 합니다.
4. Experiments
실험적으로 MixMatch의 효과를 증명합니다.
4.1 Implementation details
연구팀은 Wide ResNet-28 모델을 사용했습니다.
실험들은 다음과 같은 항목들을 제외하면 모델의 구현과 학습 절차는 Wide ResNet-28 모델과 일치한다고 합니다.
- learning rate를 decay하는 대신에 MixMatch는 decay rate가 0.999인 지수이동평균을 사용하여 모델을 평가합니다.
- Wide ResNet-28 모델의 weight decay를 매 업데이트마다 0.0004를 적용합니다.
- 개의 데이터를 훈련할 때 마다 체크포인트를 만들고 20개 체크포인트마다 에러율 중앙값을 갖습니다. 논문에서 평가 지표를 에러율로 정헀었죠.
4.2 Semi-Supervised Learning
MixMatch의 효과를 검증하기 위해 표준 벤치마크(기준) 데이터셋인 CIFAR-10, CIFAR-100, SVHN, STL-10을 이용하여 실험을 했다고 합니다.
CIFAR-10, CIFAR-100, SVHN, STL-10 데이터셋 같은 경우는 unlabel 데이터가 없습니다. 따라서 이 데이터셋의 대부분을 label 없이 사용하여 마치 unlabel 데이터처럼 사용하고, 일부분만 label 데이터로 사용했습니다.
STL-10 데이터셋 같은 경우는 5,000개의 label 이미지와 100,000개의 unlabel 이미지로 구성되어있는 준지도학습에 최적화된 데이터셋이라서 그대로 사용했다고 합니다.
4.2.1 Baseline Methods
MixMatch 알고리즘을 -Model, Mean Teacher, Virtual Adversarial Training, Pseudo-Label, MixUp baseline 방법론들이랑 비교해서 실험을 진행했습니다.
4.2.2 Results
CIFAR-10
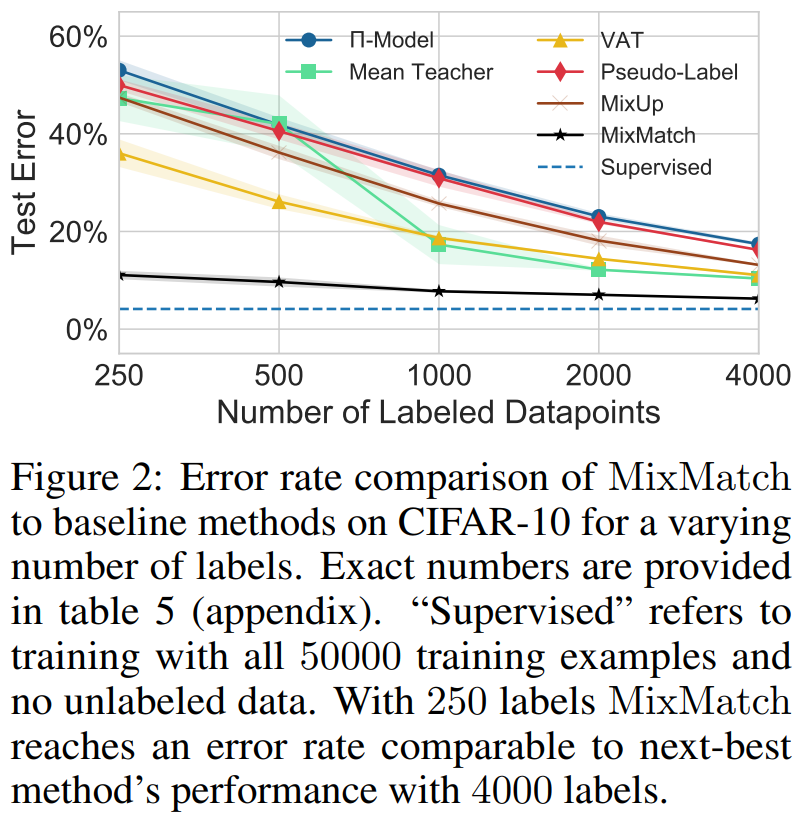
figure 2 를 보시면 x축이 데이터의 개수이고 y축이 test 에러율입니다.
지도학습의 경우 50,000개의 데이터를 학습했을 때 에러율이 4.17%입니다. (250, 500, 1000... 일 때는 측정하지 않았었는지 4.17%를 직선 형태로 갖습니다.)
반면에 MixMatch는 250개의 데이터를 학습했을 때 11.08% 였고 4,000개의 데이터를 학습했을 때는 6.24%까지 줄었습니다.
VAT와 비교해보면 250개의 데이터를 학습했을 때 36.03%으로 MixMath에 비해 4.5배나 큰 에러율을 갖습니다.
Mean Teacher와 비교해보면 4,000개의 데이터를 학습했을 때 10.36%으로 MixMatch는 250개의 데이터일 때 갖었던 에러율이죠. 데이터양이 1/16일 때 얻은 결과입니다.
CIFAR-10 and CIFAR-100 with a larger model
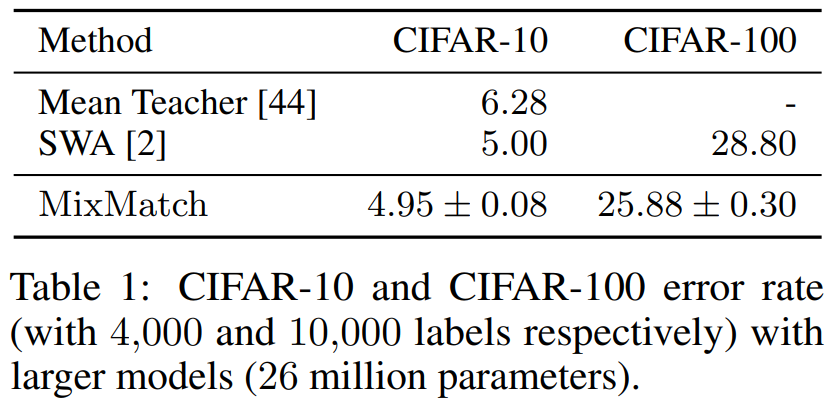
CIFAR-10과 CIFAR-100 두 개의 데이터셋으로 비교실험을 하였습니다.
Table 1.을 보면 SWA라는 용어가 나오는데 이것은 Stochastic Weight Averaging을 듯합니다.
CIFAR-10은 4,000개의 데이터를 이용해서 실험을 진행했고, CIFAR-100은 10,000개의 데이터를 이용해서 실험을 진행했다고 합니다.
동일한 조건하에서 MixMatch가 Mean Teacher와 SWA보다 더 적은 에러율을 보였습니다.
SVHN and SVHN+Extra
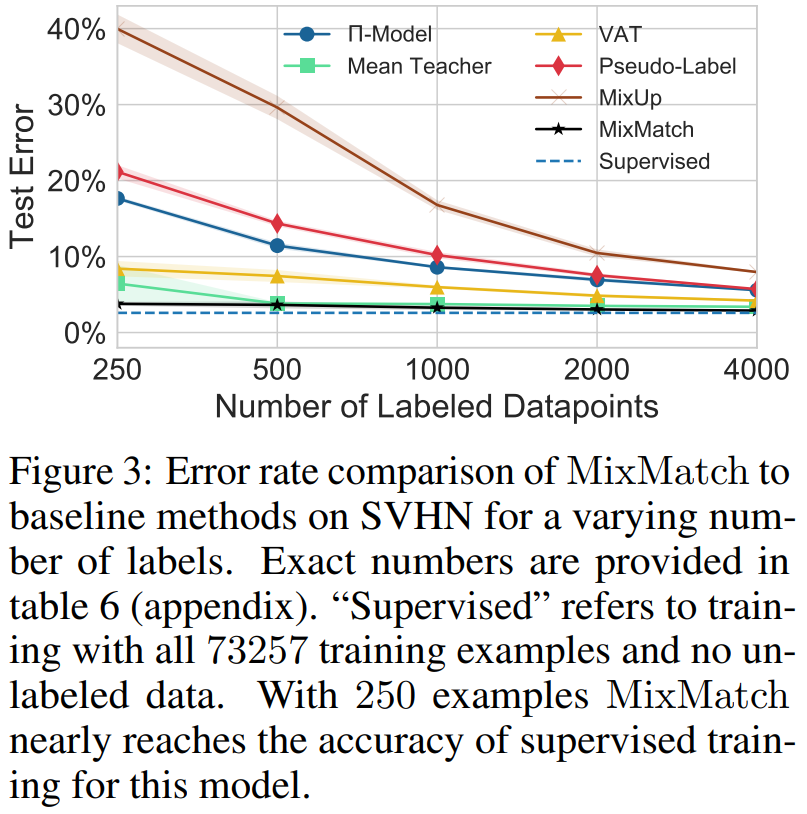
이 실험에서는 SVHN 데이터셋 73,257개의 이미지를 이용하여 각 방법론들을 비교하였습니다.
위의 figure 2와 같이 250개부터 시작해서 2배씩 증가했을 때 체크포인트를 두어 에러율을 관찰했습니다.
figure 2와 비슷하지만 다른 점은 와 다르게 로 설정하였다는 것입니다.
그러면 에서 볼 수 있듯이 unlabel 데이터에 대한 손실함수에 비중을 더 크게 두었다는 볼 수 있습니다.
SVHN 데이터셋에 대한 MixMatch의 에러율이 지도학습의 에러율과 유사하게 직선 형태를 갖는 것을 볼 수 있습니다.

그리고 알아둬야 할 점이 SVHN 데이터셋에는 train과 extra라는 학습데이터셋이 나뉜다는겁니다.
지도학습 시에는 train과 extra를 합쳐서 604,388개의 이미지를 이용해서 훈련하지만, 준지도학습 시에는 73,257만 사용한다는 것입니다.
그래서 SVHN(train)과 SVHN(train) + Extra를 비교하였습니다. unlabel 데이터의 개수 차이가 어떤 성능을 보이는지 파악하면 됩니다.
250개의 데이터를 학습했을 때부터 unlabel 데이터 비중이 높은 SVHN+Extra가 에러율이 낮았습니다.
최종 4,000개의 데이터를 학습했을 때도 SVHN+Extra가 에러율이 낮습니다.
추가적으로 73,257개의 SVHN 데이터셋을 다 마무리 지었을 때는 2.59% 에러율을 보이지만, 604,388개의 SVHN+Extra 데이터셋을 다 마무리 지었을 때는 1.71% 에러율로 훨씬 좋은 효과를 보였습니다.
이 실험으로 알 수 있는 것은 추가적인 250개의 label 데이터를 확보하여 학습하는 것보다 현재 보유한 label 데이터셋(73,257)의 8배 많은 unlabel 데이터를 확보하고 MixMatch로 label을 guessing해주어 학습하는 것이 더 좋은 성능을 가져온다는 것입니다.
결론적으로 저자가 말하고자 하는 것은 MixMatch로 unlabel 데이터에게 label을 부여하여 학습에 사용하는 것이 더 효과적이라는 것입니다.
STL-10
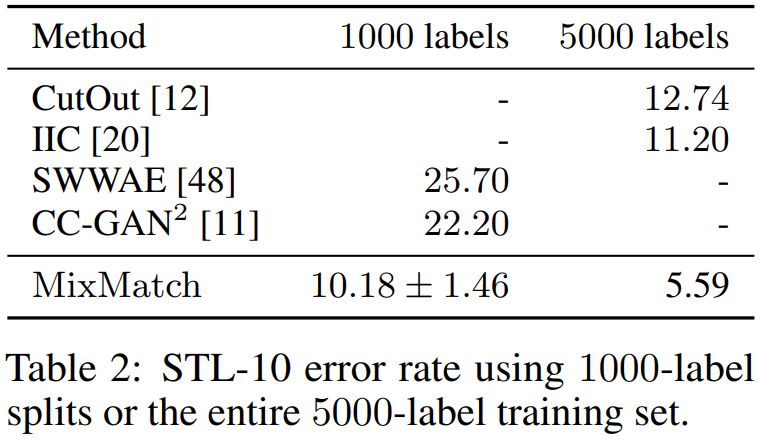
이 데이터셋은 5,000개의 학습데이터셋밖에 없는 소규모의 데이터셋입니다.
그런데 저자가 이 데이터셋을 이용한 이유는 몇가지 준지도학습 방법론들이 이 데이터셋을 사용하여서 이 방법론들과 비교실험을 하려고 사용하였습니다.
Table 2를 보시면 표가 듬성듬성 채워져있는데
실제로 CutOut, IIC 알고리즘은 5,000개의 데이터를 사용한 실험만 했었고, SWWAE, CC-GAN2 알고리즘은 1,000개의 데이터를 사용한 실험만 진행하였습니다.
그래서 MixMatch가 1,000개를 이용한 실험과 5,000개를 이용한 실험을 두 번 진행했습니다.
으로 설정하여 에서 이전 데이터셋들과 다르게 unlabel데이터에 대한 손실함수의 비중을 줄여서 실험했습니다.
MixMatch가 모든 알고리즘의 에러율에 약 1/2에 해당하는 에러율을 도출했습니다.
4.2.3 Ablation Study
MixMatch는 여러가지 준지도학습 알고리즘을 합성한 알고리즘이기 때문에 그 여러가지 알고리즘 중 하나를 제거했을 때 어떠한 성능이 나오는지 알기 위해 ablation study를 진행하였습니다.

이 실험은 CIFAR-10 데이터셋에 250개의 데이터를 학습했을 때와 최종 4,000개의 데이터를 학습했을 때의 에러율을 비교하였습니다.
이와 같이 알고리즘을 하나씩 제거하거나 변경해보았을 때 에러율이 얼마나 차이나는지를 확인할 수 있습니다.
표의 마지막 행에 Interpolation Consistency Training이 무엇인지 모르실 수 있습니다.
Interpolation Consistency Training은 unlabel 데이터만 MixUp하고 Sharpening 알고리즘을 제거하고, unlabel 데이터에 label을 guess할 때 Exponential Moving Average를 이용한 방법을 말합니다.
가장 높은 에러율을 보였습니다.
4.3 Privacy-Preserving Learning and Generalization
5. Conclusion
준지도학습 분야의 유명했던 알고리즘들을 결합하여 하나의 알고리즘으로 MixMatch를 만들었습니다.
저자는 추후에 더 많은 알고리즘들을 더 결합해서 새로운 뒤따르는 연구를 해보겠다고 합니다.
나의 생각
MixMatch라는 알고리즘은 되게 매력적인 것 같다.
나는 준지도학습 알고리즘을 self-training밖에 연구해보지 못했는데 다른 준지도학습 알고리즘을 배우게 되어 좋은 기회였고 경험이었다.
HSV를 바꿔준다거나, scaling을 한다거나 cropping 등 다양한 증강 기법을 적용해서 unlabel 데이터를 번 증강하여 classifier 모델의 prediction 결과들을 평균내서 sharpening 기법을 적용하여 그 결과를 augmentation 하기 전 unlabel 데이터의 class distribution으로 갖는다는 게 색달랐다.
어차피 번 증강을 해도 class distribution이 극변하지는 않을 것 같아 충분한 좋은 알고리즘같다.
self-training 알고리즘의 경우 단 한 번의 confidence score를 계산하여 class를 부여하여 단 한 번이 잘못 classification하였다면 잘못된 학습으로 진행되겠지만, 번 classification하고 평균을 내기 때문에 class를 잘못 부여할 확률이 낮을 것 같다.