ICP Point-To-Point, Point-To-Plane Least squares(CPP 코드 포함)

haeryong·2023년 12월 7일
0
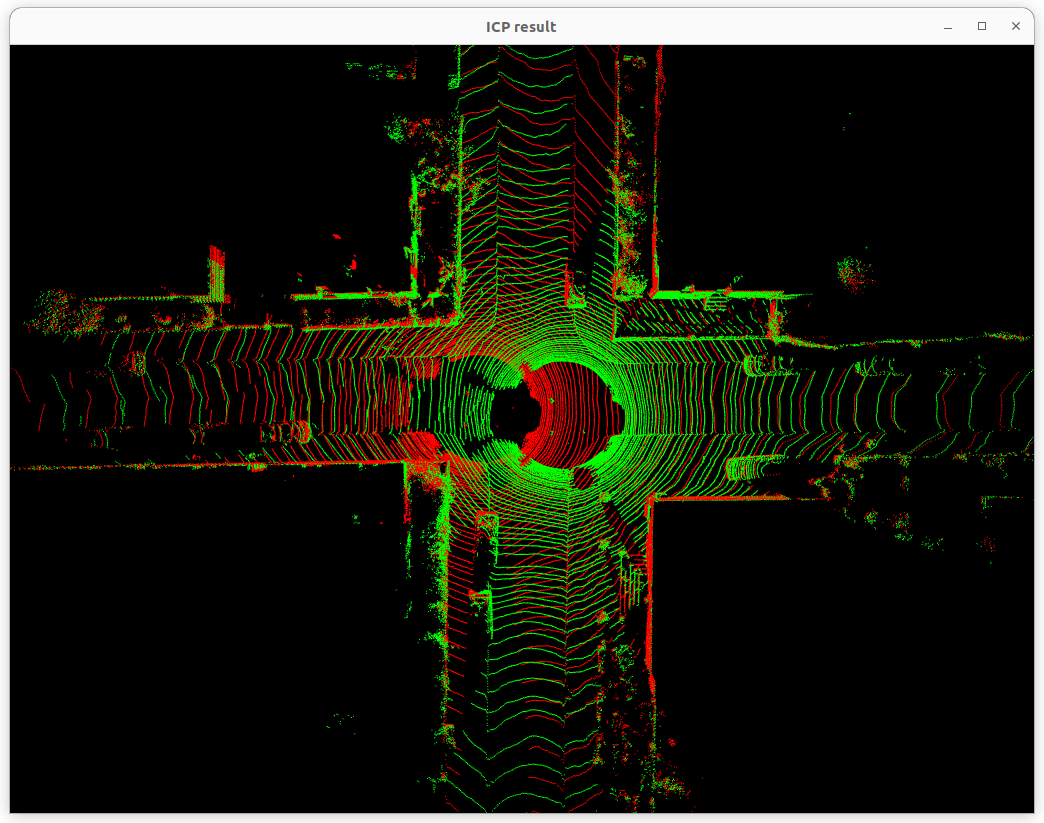
post-thumbnail

ICP Algorithm

두 점군 사이의 Euclidean Transform을 계산하는 ICP 알고리즘은 Point-to-Point, Point-to-Plane, Generalized ICP, VGICP 등 다양한 버전이 존재한다.

그 중 살펴볼 것은 가장 기본적인 Point-to-Point, Point-to-Plane 알고리즘인데, Point-to-Point, Point-to-Plane 방법을 최소제곱법을 이용해서 푸는 과정을 살펴보겠다.

여기서 살펴볼 부분은 두 포인트클라우드 사이의 매칭을 완료한 뒤에 최소제곱법을 이용해서 최적의 T를 계산하는 부분이다.

전체 ICP 알고리즘은 correspondence matching과 compute Transform를 반복해서 정합을 수행한다. KITTI 데이터셋을 이용한 ICP 알고리즘은 아래 github에서 볼 수 있다.

https://github.com/LimHaeryong/ICP-Implementation/tree/main

1. Point to Point

두 점군 P={p1,p2,p3,...},Q={q1,q2,q3,...}P=\{p_1,p_2,p_3,...\},\quad Q=\{q_1,q_2,q_3,...\}이 있을 때,

최적의 T를 계산하기 위해 우리는 residual의 제곱합을 최소화하는 T를 찾아야 한다.
Point-to-Point 방법에서 residual은 매칭된 두 점 사이의 거리이다.

T∗=argminTΣ∣∣T∗pi−qi∣∣2=argminTΣ∣∣R∗pi+t−qi∣∣2=argminTΣ∣∣residuali∣∣2T^*=argmin_T\Sigma||T*p_i-q_i||^2=argmin_T\Sigma||R*p_i+t-q_i||^2=argmin_T\Sigma||residual_i||^2

여기서 회전 R을 x축에 대해 α\alpha만큼, y축에 대해 β\beta만큼, z축에 대해 γ\gamma만큼 회전하는 세 회전 행렬의 곱이라고 생각하면,

R(α,β,γ)=Rz(γ)∗Ry(β)∗Rx(α)=(cos(γ)cos(β)−sin(γ)∗cos(α)+cos(γ)∗sin(β)∗sin(α)sin(γ)sin(α)+cos(γ)sin(β)cos(α)sin(γ)cos(β)cos(γ)cos(α)+sin(γ)sin(β)sin(α)−cos(γ)sin(α)+sin(γ)sin(β)cos(α)−sin(β)cos(β)sin(α)cos(β)cos(α))R(\alpha,\beta,\gamma)=R_z(\gamma)*R_y(\beta)*R_x(\alpha)=\begin{pmatrix}cos(\gamma)cos(\beta)&-sin(\gamma)*cos(\alpha)+cos(\gamma)*sin(\beta)*sin(\alpha)&sin(\gamma)sin(\alpha)+cos(\gamma)sin(\beta)cos(\alpha)\\sin(\gamma)cos(\beta)&cos(\gamma)cos(\alpha)+sin(\gamma)sin(\beta)sin(\alpha)&-cos(\gamma)sin(\alpha)+sin(\gamma)sin(\beta)cos(\alpha)\\-sin(\beta)&cos(\beta)sin(\alpha)&cos(\beta)cos(\alpha)\end{pmatrix}

인데, 여기서 회전의 크기가 작다는 가정 하에 sin(θ)≈θ,cos(θ)≈1,sin(θ)sin(ϕ)≈0sin(\theta)\approx\theta,\quad cos(\theta)\approx1,\quad sin(\theta)sin(\phi)\approx0을 R에 적용하면 아래를 얻는다.

R=(1−γβγ1−α−βα1)=I+[r]skew,r=(α,β,γ)TR=\begin{pmatrix}1&-\gamma&\beta\\ \gamma & 1 & -\alpha\\-\beta&\alpha&1\end{pmatrix} = I+[r]_{skew},\quad r=(\alpha,\beta,\gamma)^T

Skew symmetric

[v]skew=(0−vzvyvz0−vx−vyvx0)[v]_{skew}=\begin{pmatrix}0&-v_z&v_y\\v_z&0&-v_x\\-v_y&v_x&0\end{pmatrix}는 벡터 vv에 대한 skew symmetric matrix이다.

벡터 a의 skew symmetric과 b의 곱은 a와 b에대한 외적과 같다.
[a]skewb=a×b=−b×a=−[b]skewa[a]_{skew}b=a\times b=-b\times a=-[b]_{skew}a

residuali=R∗pi+t−qi=pi+[r]skewpi+t−qi=−[pi]skewr+t+pi−qiresidual_i=R*p_i+t-q_i=p_i+[r]_{skew}p_i+t-q_i=-[p_i]_{skew}r+t+p_i-q_i

여기서 x=(tx,ty,tz,α,β,γ)Tx=(t_x,t_y,t_z,\alpha,\beta,\gamma)^T라 할 때, 위 식은 아래와 같이 다시 쓸 수 있다.

residuali=(I−[pi]skew)x+(pi−qi)=Aix+biresidual_i=\begin{pmatrix}I&-[p_i]_{skew}\end{pmatrix}x+(p_i-q_i)=A_ix+b_i

∣∣residuali∣∣2=xTAiTAix+2xTATb+bTb||residual_i||^2=x^TA_i^TA_ix+2x^TA^Tb+b^Tb이고,

∂∣∣residuali∣∣2∂x=2∗AiTAix+2AiTbi\frac{\partial ||residual_i||^2}{\partial x}=2*A^T_iA_ix+2A^T_ib_i이다.

Σ∣∣residuali∣∣2\Sigma||residual_i||^2이 최소가 되려면 Σ∂∣∣residuali∣∣2∂x=0\Sigma\frac{\partial ||residual_i||^2}{\partial x}=0을 만족해야한다.

따라서 아래 식을 풀면 최적의 x, 최적의 T를 얻을 수 있다.

Σ(AiTAi)x+Σ(AiTbi)=Cx+d=0\Sigma(A_i^TA_i)x+\Sigma(A_i^Tb_i)= Cx+d =0

이 때, 6 by 6 행렬 C는 Positive-definite, Symmetric Matrix이므로, LDLTLDL^T 분해를 사용해 최적의 x를 구할 수 있다.

Weight, Robust Kernel
각 residual에 가중치를 적용해 weighted squared sum을 최소화하는 문제를 생각해볼 수 있다.

T=argminTΣwi∗∣∣residuali∣∣2T=argmin_T\Sigma w_i*||residual_i||^2

wiw_i가 x와 관련이 없다고 가정할 때, Cx+d=Σ(wiAiTAi)x+Σ(wiAiTbi)=0Cx+d=\Sigma(w_iA_i^TA_i)x+\Sigma(w_iA_i^Tb_i)=0이 된다.

wiw_i을 residual에 대한 loss function을 사용할 수 있는데, 이는 ICP문제에서 자주 발생하는 outlier를 제거해주는 효과를 가진다.

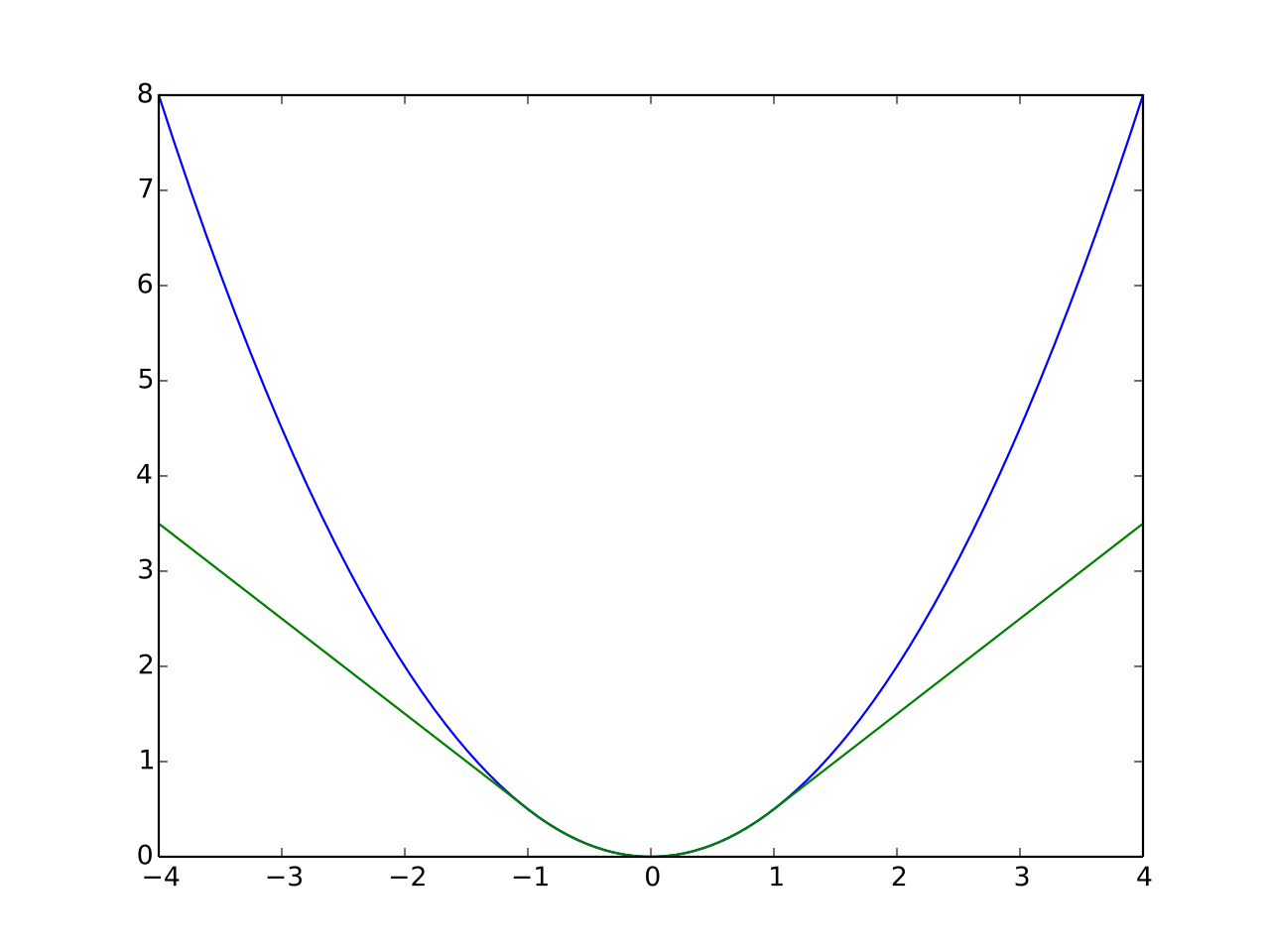
위 그래프의 파란 선은 가중치가 없을 때(L2 loss)이고, 녹색 선은 Huber loss이다. 적절한 loss function을 사용해 residual이 커질 때 전체 cost function이 과도하게 커지는 것을 방지할 수 있다. 즉 outlier를 제거하는 효과를 기대할 수 있다.

  • point_to_point.cpp 코드
#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>

#include <Eigen/Dense>

Eigen::Matrix3d createRotationMatrix(const Eigen::Vector3d &r);
Eigen::Matrix3d skewSymmetric(const Eigen::Vector3d &vec);
std::pair<Eigen::Matrix<double, 3, 6>, Eigen::Vector3d> compute_Ai_and_bi(const Eigen::Vector3d &pi, const Eigen::Vector3d &qi);
// German-McClure loss function
double GMLoss(double k, double residual);
std::pair<Eigen::Vector3d, Eigen::Vector3d> computeTransform(const std::vector<Eigen::Vector3d> &P, const std::vector<Eigen::Vector3d> &Q);

int main()
{
    // Transform to estimate.
    Eigen::Vector3d r(5.0 * M_PI / 180.0, 4.0 * M_PI / 180.0, 3.0 * M_PI / 180.0);
    Eigen::Matrix3d R = createRotationMatrix(r);
    Eigen::Vector3d translation(10.0, 20.0, 30.0);

    Eigen::Matrix4d transform = Eigen::Matrix4d::Identity();
    transform.block<3, 3>(0, 0) = R;
    transform.block<3, 1>(0, 3) = translation;

    std::cout << "Transform Matrix \n" << transform << '\n'; 

    // Test dataset
    std::vector<Eigen::Vector3d> P(50), Q(50);
    for (int i = 0; i < 50; ++i)
        P[i].setRandom();
    for (int i = 0; i < 50; ++i)
        Q[i] = R * P[i] + translation;

    Eigen::Matrix4d transform_est = Eigen::Matrix4d::Identity();

    for (int i = 0; i < 200; ++i)
    {
        auto [t_est_iter, r_est_iter] = computeTransform(P, Q);
        auto R_est_iter = createRotationMatrix(r_est_iter);
        Eigen::Matrix4d transform_est_iter = Eigen::Matrix4d::Identity();
        transform_est_iter.block<3, 3>(0, 0) = R_est_iter;
        transform_est_iter.block<3, 1>(0, 3) = t_est_iter;
        transform_est = transform_est_iter * transform_est;
        std::cout << i + 1 << "'th estimated transform = \n" << transform_est << '\n';
        for (auto &p : P)
            p = R_est_iter * p + t_est_iter;
    }

    std::cout << "Transform Matrix \n" << transform << '\n'; 

    return 0;
}

Eigen::Matrix3d createRotationMatrix(const Eigen::Vector3d &r)
{
    Eigen::AngleAxisd rotationX(r[0], Eigen::Vector3d::UnitX());
    Eigen::AngleAxisd rotationY(r[1], Eigen::Vector3d::UnitY());
    Eigen::AngleAxisd rotationZ(r[2], Eigen::Vector3d::UnitZ());
    Eigen::Matrix3d rotationMatrix = (rotationZ * rotationY * rotationX).toRotationMatrix();

    return rotationMatrix;
}

Eigen::Matrix3d skewSymmetric(const Eigen::Vector3d &vec)
{
    Eigen::Matrix3d skew;
    skew << 0.0, -vec[2], vec[1],
        vec[2], 0.0, -vec[0],
        -vec[1], vec[0], 0.0;
    return skew;
}

std::pair<Eigen::Matrix<double, 3, 6>, Eigen::Vector3d> compute_Ai_and_bi(const Eigen::Vector3d &pi, const Eigen::Vector3d &qi)
{
    Eigen::Matrix<double, 3, 6> Ai;
    Eigen::Vector3d bi;

    Ai.block<3, 3>(0, 0) = Eigen::Matrix3d::Identity();
    Ai.block<3, 3>(0, 3) = -1.0 * skewSymmetric(pi);

    bi = pi - qi;

    return std::make_pair(Ai, bi);
}

double GMLoss(double k, double residual_sq)
{
    return k / std::pow(k + residual_sq, 2.0);
}

std::pair<Eigen::Vector3d, Eigen::Vector3d> computeTransform(const std::vector<Eigen::Vector3d> &P, const std::vector<Eigen::Vector3d> &Q)
{
    Eigen::Matrix<double, 6, 6> C;
    Eigen::Vector<double, 6> d;
    C.setZero();
    d.setZero();

    for (size_t i = 0; i < P.size(); ++i)
    {
        auto [Ai, bi] = compute_Ai_and_bi(P[i], Q[i]);
        //double wi = GMLoss(3.0, (P[i] - Q[i]).squaredNorm());
        double wi = 1.0;
        C += wi * Ai.transpose() * Ai;
        d += wi * Ai.transpose() * bi;
    }

    Eigen::Vector<double, 6> x_opt = C.ldlt().solve(-d);

    return std::make_pair(x_opt.head(3), x_opt.tail(3));
}
  • 결과

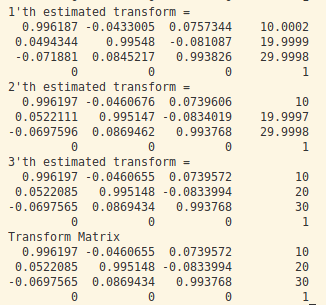
위에서 설명한 transform을 구하는 함수를 iterative하게 적용해 2~3번의 반복만에 동일한 결과를 얻었다.
outlier가 존재하지 않기 때문에 loss는 적용하지 않았지만 실제 데이터셋에는 loss를 추가해야 더 좋은 결과를 얻을 수 있다.

2. Point to Plane

Point to Plane 방식을 사용하기 위해서는 두 점군 P, Q 중 하나의 점군은 점의 위치 뿐만아니라 normal vector를 함께 계산해야한다. 여기서는 점군 Q의 normal vector가 계산되었다고 생각한다.

normal vector는 보통 점군에서 nearest search를 이용해서 이웃한 점들을 찾고, 이를 이용해서 Normal Estimation을 수행한다. 최소 3개의 점이 있으면 하나의 평면을 추정할 수 있고, 더 많은 점을 이용해 RANSAC 기법 등을 사용해 더 Robust하게 Normal vector를 얻어낼 수 있다.

비용함수는 아래와 같다. 여기서 residual은 두 점을 뺀 벡터와 normal vector의 내적과 같다.
T∗=argminTΣ∣∣(T∗pi−qi)⋅ni∣∣2=argminTΣ∣∣(R∗pi+t−qi)⋅ni∣∣2=argminTΣ∣∣residuali∣∣2T^*=argmin_T\Sigma||(T*p_i-q_i)\cdot n_i ||^2=argmin_T\Sigma||(R*p_i+t-q_i)\cdot n_i||^2=argmin_T\Sigma||residual_i||^2

residuali=niT(I−[pi]skew)x+niT(pi−qi)=(niT(pi×ni)T)x+niT(pi−qi)=Aix+biresidual_i=n_i^T\begin{pmatrix}I&-[p_i]_{skew}\end{pmatrix}x+n_i^T(p_i-q_i)=\begin{pmatrix}n_i^T&(p_i\times n_i)^T\end{pmatrix}x+n_i^T(p_i-q_i)=A_ix+b_i

AiA_i가 3 by 6에서 1 by 6이 되었고, bib_i가 크기 3에서 크기 1인 벡터가 되었지만 이후의 과정은 Point to Point와 동일하다.

실제 Pointcloud scan을 사용하지 않으면 normal vector 등을 재현하기 힘들기 때문에 Point to Plane 버전의 computeTransform 예시 코드만 작성해두었다.

  • point_to_plane.cpp 예시 코드
std::pair<Eigen::Matrix<double, 1, 6>, Eigen::Vector<double, 1>> compute_Ai_and_bi(const Eigen::Vector3d &pi, const Eigen::Vector3d &qi, const Eigen::Vector3d& q_norm_i)
{
    Eigen::Matrix<double, 1, 6> Ai;
    Eigen::Vector<double, 1> bi;

    Ai.block<1, 3>(0, 0) = q_norm_i.transpose();
    Ai.block<1, 3>(0, 3) = pi.cross(q_norm_i).transpose();

    bi = (pi - qi).transpose() * q_norm_i;

    return std::make_pair(Ai, bi);
}


std::pair<Eigen::Vector3d, Eigen::Vector3d> computeTransform(const std::vector<Eigen::Vector3d> &P, const std::vector<std::pair<Eigen::Vector3d, Eigen::Vector3d>> &Q)
{
    Eigen::Matrix<double, 6, 6> C;
    Eigen::Vector<double, 6> d;
    C.setZero();
    d.setZero();

    for (size_t i = 0; i < P.size(); ++i)
    {
    	const auto& [q, q_norm] = Q[i];
        auto [Ai, bi] = compute_Ai_and_bi(P[i], q, q_norm);
        //double wi = GMLoss(3.0, (P[i] - q).squaredNorm());
        double wi = 1.0;
        C += wi * Ai.transpose() * Ai;
        d += wi * Ai.transpose() * bi;
    }

    Eigen::Vector<double, 6> x_opt = C.ldlt().solve(-d);

    return std::make_pair(x_opt.head(3), x_opt.tail(3));
}

3. 성능 향상

Eigen library의 경우 2중 배열같은 row major 방식이 아닌 column major 방식이다. 따라서 예제 코드에 Ai를 계산하는 대신 Ai의 transpose를 계산하는 식으로 변경하면 계산 속도를 높일 수도 있을 것 같다.

또한 실제 라이다 스캔을 정합하는 경우 점의 개수가 매우 많기 때문에 thread, tbb, openmp 등의 병렬 프로그래밍을 통해 속도를 향상시킬 수 있다.

아래 코드는 computeTransform에 OpenMP를 적용한 코드이다.

  • point_to_point_omp.cpp
#include <omp.h>


std::pair<Eigen::Vector3d, Eigen::Vector3d> computeTransform(const std::vector<Eigen::Vector3d> &P, const std::vector<Eigen::Vector3d> &Q)
{
    Eigen::Matrix<double, 6, 6> C;
    Eigen::Vector<double, 6> d;
    C.setZero();
    d.setZero();

#pragma omp parallel
    {
        Eigen::Matrix<double, 6, 6> C_private;
        Eigen::Vector<double, 6> d_private;
        C_private.setZero();
        d_private.setZero();
#pragma omp for nowait
        for (size_t i = 0; i < P.size(); ++i)
        {
            auto [Ai, bi] = compute_Ai_and_bi(P[i], Q[i]);
            // double wi = GMLoss(3.0, (P[i] - Q[i]).squaredNorm());
            double wi = 1.0;
            C_private += wi * Ai.transpose() * Ai;
            d_private += wi * Ai.transpose() * bi;
        }
#pragma omp critical 
        {
            C += C_private;
            d += d_private;
        }
    }

    Eigen::Vector<double, 6> x_opt = C.ldlt().solve(-d);

    return std::make_pair(x_opt.head(3), x_opt.tail(3));
}
profile
haeryong
이전 포스트

[Ceres-Solver] Rotation과 Manifold

다음 포스트

리 군, 리 대수 정리

0개의 댓글