[Ceres-Solver] Rotation과 Manifold

haeryong·2023년 12월 3일

1. 3차원 회전

아래와 같은 다양한 방법으로 3차원 회전 기술할 수 있다.

Euler Angles : 3차원 벡터를 사용하며, 각 원소는 x축, y축, z축 방향의 회전의 크기가 된다.

Angle-Axis, Rotation Vector : 3차원 벡터를 사용하며, 벡터의 방향이 회전축이 되고, 벡터의 norm이 회전의 크기가 된다. Rotation Vector의 norm과 방향을 분리해 4개의 파라미터를 사용할 수도 있다.

Quaternion : 4개의 원소를 사용하며, norm이 1인 Unit quaternion을 이용해 회전을 기술한다.

Rotation Matrix : 3by3 행렬을 사용하며, Orthogonal Matrix 중 determinent=1인 행렬을 이용해 회전을 기술한다.

Rotation	Parameters	Constraints
Euler Angles	$(\phi,\theta,\psi)$	$[0,2\pi)\times[-\pi/2,\pi/2]\times[0,2\pi)$
Angle-Axis	$(v_1,v_2,v_3,\theta)$	$S^2\times[0,\pi)$
Rotation Vector	$(r_1,r_2,r_3)$	None
Quaternion	$(q_0,q_1,q_2,q_3)$	$q_0^2+q_1^2+q_2^2+q_3^2=1$
Rotation Matrix	$3\times3$ Matrix	$RR^T=I$ , $det(R)=1$

1.1 Singularity

Euler Angles : 짐벌락. roll-pitch-yaw convention 기준 pitch가 $\pm\pi/2$ 일 때, roll, yaw axis가 정렬되어 동일한 회전에 대해 무수히 많은 해가 존재한다. 항등 회전의 경우 무수히 많은
Angle-Axis : 회전 각도가 180도일 때, 반대 방향으로 180도 회전하는 것과 동일한 모호성 문제가 발생한다.
Quaternion : unit quaternion은 SO(3)의 double covering으로, 항상 R(-q) = R(q)을 만족하며, 하나의 회전에 대해 2가지 쿼터니언 해가 존재한다.
Rotation Matrix : 없음

이 방식들 중 쿼터니언은 Singularity 문제가 간단한 편이고, Rotation Matrix에 비해 제약조건과 파라미터의 수가(4개) 적기 때문에 계산 비용이 적다는 장점이 있다.

Angle-Axis와 달리, Quaternion은 Unit Quaternion 제약조건이 존재하는데, Ceres-Solver를 이용해 비선형최적화를 수행할 때 이 부분을 고려하지 않으면 Cost Function은 최소가 되지만 Unit Quaternion 조건을 만족하지 않는 부정확한 결과를 얻게 된다.

2. Manifold

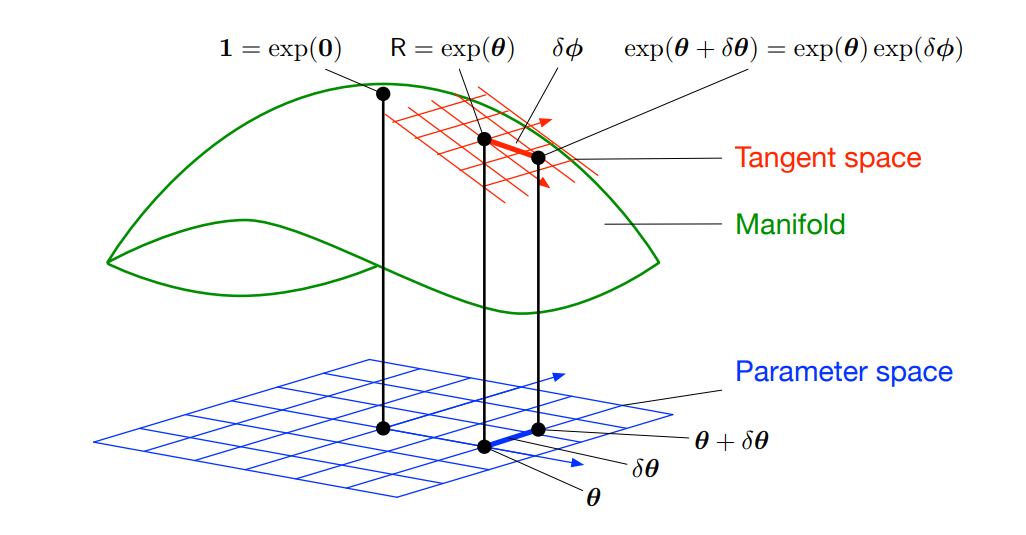
Unit Quaternion은 4차원 공간의 반지름이 1인 구 위의 점들의 집합으로 표현되는데, 이 미분가능한 곡면을 (Smooth)Manifold라 한다. 또한 Manifold 상의 각각의 점마다 Manifold에 접하는 평면 Tangent Space을 구할 수 있으며, Tangent Space를 이용해 제약조건이 있는 최적화 문제를 제약조건을 없애서 더 쉽게 계산할 수 있다.

출처

예를 들어 주어진 Manifold가 3차원 공간상의 반지름이 1인 구라고 할 때, 매 iteration마다 현재 위치에서 구에 접하는 2차원 Tangent Space를 구하고, Tangent Space 상에서 delta만큼 점을 이동시킨 뒤 실제 3차원 점의 위치를 계산하는 것이다. 제약조건을 가지는 Parameter(Ambient) Space와 달리 Tangent Space는 유클리디언 공간이므로 제약조건을 가지지 않는다.
Tangent Space와 Parameter Space 사이의 변환을 위해서는 Tangent Space와 Parameter Space 사이의 Plus, Minus 연산과 그에 따른 Jacobian을 Manifold 종류마다 정의해 주어야 한다.

3. Ceres::QuaternionManifold

Ceres-Solver는 QuaternionManifold를 제공하는데, 이를 이용해서 간단하게 회전에 대한 비선형 최적화를 진행할 수 있다.

Ceres::QuaternionManifold와 Ceres::EigenQuaternionManifold가 주어지는데, 이는 Eigen::Quaternion이 coefficients를 저장하는 순서와 연관이 있다.

Eigen 라이브러리의 쿼터니언은 $(q_w,q_x,q_y,q_z)$ 의 순서로 정의된 Hamilton convention을 따르지만 내부적으로 data가 저장된 순서는 $(q_x,q_y,q_z,q_w)$ 순이다. 따라서 Eigen::Quaternion을 사용하는 경우 Ceres::EigenQuaternionManifold을 사용해야 문제가 없다.

QuaternionManifold가 정의된 헤더파일을 살펴보면 Ambient Space 상의 점 x가 Tangent Space에서 delta만큼 이동했을 때 Ambient Space에서의 위치를 계산해주는 Plus, Minus 메서드가 존재하고, 그에따른 Jacobian 메서드도 정의되어 있다.

ceres-solver/include/ceres/manifold.h

...
class CERES_EXPORT EigenQuaternionManifold final : public Manifold {
 public:
  int AmbientSize() const override { return 4; }
  int TangentSize() const override { return 3; }

  bool Plus(const double* x,
            const double* delta,
            double* x_plus_delta) const override;
  bool PlusJacobian(const double* x, double* jacobian) const override;
  bool Minus(const double* y,
             const double* x,
             double* y_minus_x) const override;
  bool MinusJacobian(const double* x, double* jacobian) const override;
};
...

4. 예제 코드

2쌍의 3차원 점군 사이의 SE(3) 변환을 계산하는 예제를 간단히 작성해 보았다.
SetManifold 메서드를 호출해 EigenQuaternionManifold를 사용하도록 하였다. 결과로 얻는 quaternion은 unit quaternion 조건을 만족한다.


#include <iostream>
#include <vector>

#include <ceres/ceres.h>
#include <ceres/rotation.h>
#include <Eigen/Dense>

struct PointToPointError
{
    PointToPointError(const Eigen::Vector3d &p_source, const Eigen::Vector3d &p_target)
        : p_source_(p_source), p_target_(p_target)
    {
    }

    template <typename T>
    bool operator()(const T *const quat_ptr, const T *const translation_ptr, T *residuals) const
    {
        Eigen::Map<const Eigen::Quaternion<T>> quat(quat_ptr);
        Eigen::Map<const Eigen::Matrix<T, 3, 1>> translation(translation_ptr);

        Eigen::Matrix<T, 3, 1> p_diff = quat * p_source_.cast<T>() + translation - p_target_.cast<T>();
        residuals[0] = p_diff[0];
        residuals[1] = p_diff[1];
        residuals[2] = p_diff[2];
        return true;
    }

    static ceres::CostFunction *create(const Eigen::Vector3d &p_source, const Eigen::Vector3d &p_target)
    {
        return (new ceres::AutoDiffCostFunction<PointToPointError, 3, 4, 3>(
            new PointToPointError(p_source, p_target)));
    }
    const Eigen::Vector3d p_source_;
    const Eigen::Vector3d p_target_;
};

int main()
{
	std::vector<Eigen::Vector3d> source_points;
    std::vector<Eigen::Vector3d> target_points;
    
    ...
    add points...
    ...
	
    Eigen::Quaterniond quaternion(1.0, 0.0, 0.0, 0.0); 
    // 생성자는 w,x,y,z 순이지만 내부 data는 x,y,z,w 순서로 저장되어 있다.
    Eigen::Vector3d translation(0.0, 0.0, 0.0);
    
    ceres::Problem problem;
    
	for(int i = 0; i < source_points.size(); ++i)
    {
    	auto cost_function = PointToPointError::create(source_points[i], target_points[i]);
    	problem.AddResidualBlock(cost_function, nullptr, 
        	quaternion.coeffs().data(), translation.data());
        problem.SetManifold(quaternion.coeffs().data(), new ceres::EigenQuaternionManifold());
    }
    
    ceres::Solver::Options options;
    options.linear_solver_type = ceres::DENSE_QR;
    options.minimizer_progress_to_stdout = true;
    ceres::Solver::Summary summary;
    ceres::Solve(options, &problem, &summary);
    
    Eigen::Matrix4d transform;
    transform.block<3, 3>(0, 0) = quaternion.toRotationMatrix();
    transform.block<3, 1>(0, 3) = translation;
    
    std::cout << "final transform is " << transform << '\n';
    
	return 0;
}

haeryong

이전 포스트

[MVG] 2차원 사영변환(Homography) 추정 (+ CPP 코드)

다음 포스트