통계론

naem1023·2021년 8월 5일

ai-math

목록 보기

7/10

통계론

모수

통계적 모델링 = 적절한 가정으로 확률 분포를 추정하는 것
기계학습과 통계학이 공통적으로 추구하는 목표.

유한한 데이터만 관찰해서 모집단의 정확한 분포 예측은 불가능하다.
=> 근사적으로 확률분포 추정

모수적(parametric) 방법론

데이터가 특정 확률 분포를 따른다고 선험적(a priori)으로 가정
그 분포를 결정하는 모수(paramter)를 추정

비모수(nonparametric) 방법론

확률 분포를 미리 가정하지 않는다.
데이터에 따라 모델의 구조 및 모수의 개수를 변형

보통 모수가 무한히 많거나 계속 변형되어야 할 때 사용.

비모수 방법론이 모수를 쓰지 않는 것은 용어에 대한 오해이다.

확률 분포를 가정하는 방법

아래의 가정표를 참조하지만, 기계적으로 정하는 것이 아니라 데이터를 생성하는 원리를 고려해서 확률 분포를 정해야 한다.

데이터가 2개의 값(0, 1)만 가지는 경우 => 베르누이분포
데이터가 n개의 이산적인 값만 가지는 경우 => 카테고리분포
데이터가 [0, 1]사이에서 값을 가지는 경우 => 베타분포
데이터가 0 이상의 값을 가지는 경우 => 감마분포, 로그정규분포 등
데이터가 ℝ전체에서 값을 가지는 경우 => 정규분포, 라플라스분포 등

모수 추정

확률 분포를 가정했다면 모수를 추정할 수 있다.

가령, 정규분포의 모수는 평균과 분산이다. 이를 추정하는 통계량(statistic)은 다음과 같다.

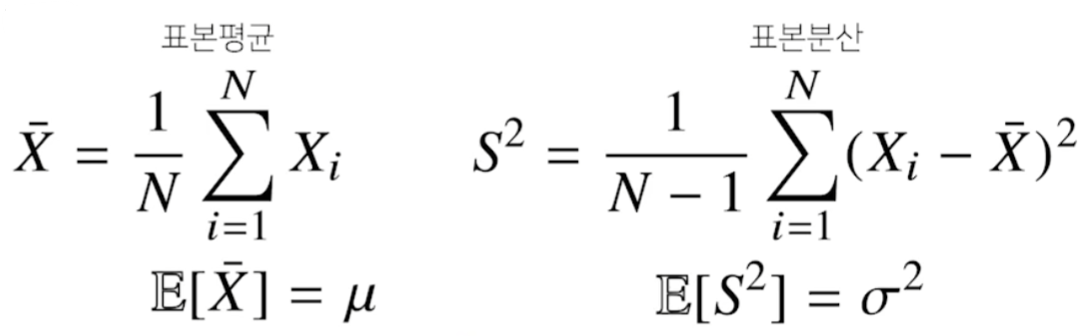
이상적이라면 표본평균은 본래 데이터인 모집단의 평균과 일치한다.

분산을 구할 때 N-1로 나누는 이유를 대학교 때 배웠는데.. 기억에서 삭제됐다. 나중에 찾아봐야겠다.

부캠 강의에서는 불편(unbiased) 추정량을 구하기 위함이라고만 설명하고 넘어갔다.

표집분포(Sampling distribution)

표집분포 = 통계량(표본평균, 표본분산)의 확률분포
표본분포 = 모집단의 분포

표집분포(sampling distribution)과 표본분포(sample distribution)은 다르다.

중심극한정리(central limit theorem)

표본평균의 표집분포는 N(데이터의 수)가 커질수록 정규분포를 따른다.

모집단의 분포가 정규분포를 따르지 않아도 성립한다.

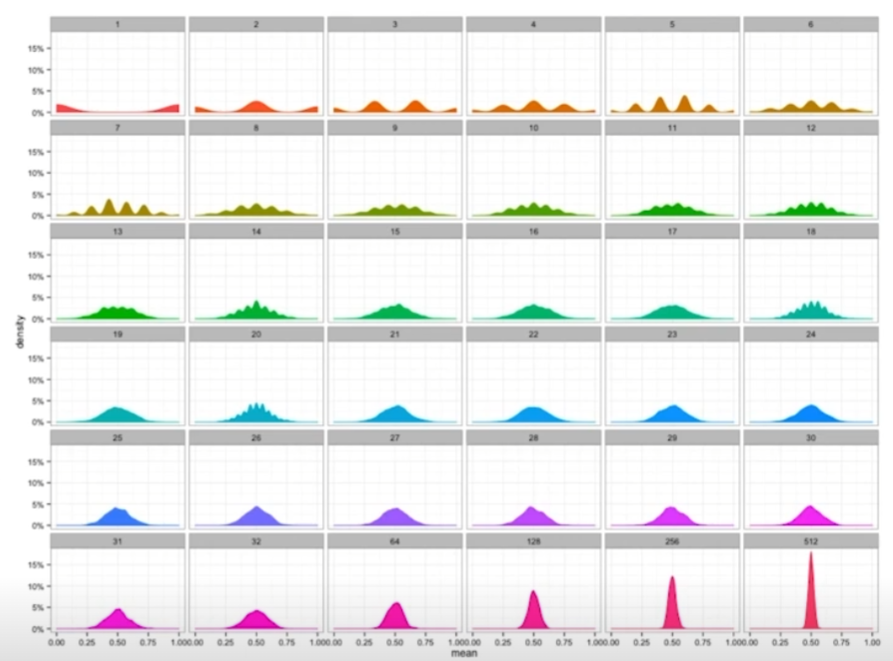
위 그림의 모집단은 베르누이분포(이항분포)이다. 즉, 모집단을 아무리 모아봤자 정규분포를 따르지 않는다.

하지만 모집단의 통계량에 대한 확률분포는 N이 커질수록 분산이 0에 가까워지면서 정규분포를 따르는 것을 볼 수 있다.

최대가능도 추정법(MLE)

MLE(Maximum likelihood estimation)

이론적으로 가장 가능성이 높은 모수를 측정하는 방법.

가능도함수

가능도함수(Likelihood function) = L(Θ;x)
확률질량함수, 확률밀도함수랑 같은 의미이지만 다른 관점을 가진 것이다.

확률밀도함수 = 모수 Θ가 주어져을 때, x에 대한 함수
가능도함수 = 변수 x가 주어졌을 때, 모수 Θ에 대한 함수

즉, 가능도함수는 변수가 미리 주어졌을 때, 모수 Θ에 대해서 변화하는 함수이다.

모수 Θ를 따르는 분포가 데이터 x를 관찰할 가능성을 뜻한다.

전체 범위에 대한 적분을 하거나 급수를 구했을 때 1이되는 확률이 아니다. 단지, 대소 비교가 가능한 관찰 가능한 가능성일 뿐이다.

로그가능도(Log likelihood)

데이터 집합 X가 독립적으로 추출되었을 경우 아래와 같이 Likelihood 함수를 정의할 수 있다.

이 때, product로 정의되는 likelihood 함수에 로그를 씌워져서 가능성들의 합으로 정의하여 사용하기도 한다.
이것이 로그가능도이고 보통 이것을 최적화한다.

로그가능도을 사용하는 이유

연산의 가능성
- 데이터가 매우 많을 때, 가능도를 곱셈으로만 정의하면 컴퓨터가 정확도를 보장할 수 없는 경우도 발생한다.
- 하지만 로그가능도를 통해 덧셈으로만 가능도를 정의하면 컴퓨터로 연산이 가능하며 정확도를 보장할 수 있다.
gradient descent에서 미분 연산의 알고리즘 효율성
- 곱셈으로만 가능도를 정의하면 연산량은 O(n²)이다.
- 덧셈으로만 가능도를 정의한 로그가능도의 연산량은 O(n)이다.

gradient descent를 사용할 때는, 음의 로그가능도(negative log likelihood)를 사용한다.

정규분포의 최대가능도 측정법 예제

정규분포를 따르는 확률변수 X로부터 독립적인 표본 {x1, ... , xn}을 얻었다고 가정해보자.

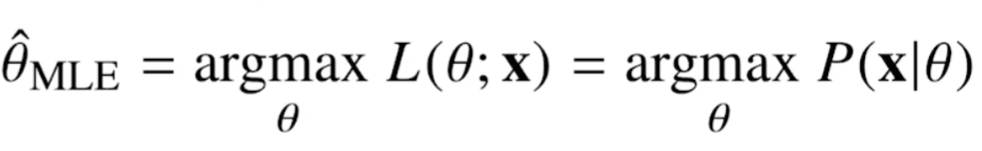
목표 : Likelihood 함수를 최적화하는 Θ를 찾는 것

정규분포를 따르는 데이터이기 때문에 Θ=(평균(뮤), 분산(시그마 제곱))으로 생각해보자. 특수기호 따오는게 귀찮아서 한글로 대체.

likelihood 함수에 로그를 씌워주면 곱셈으로 엮인 정규분포 식이 덧셈으로 분해된다.

이를 평균과 분산에 대해 각각 미분하면 아래와 같다.

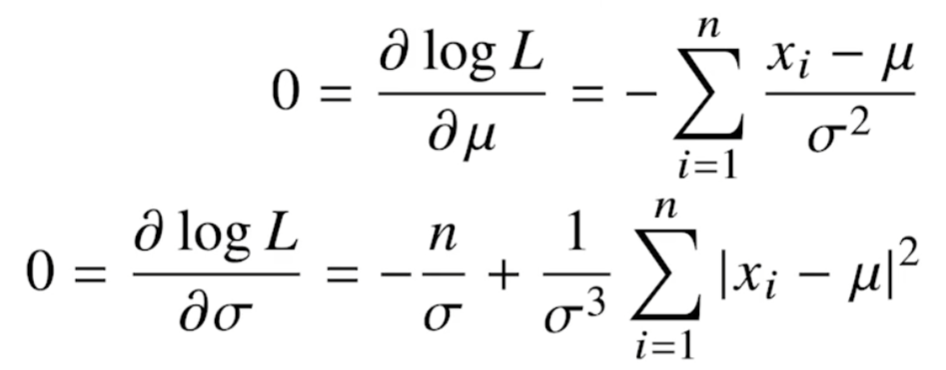
두 미분식이 모두 0이 되는 뮤와 시그마를 찾으면 likelihood를 최대화하게된다. 두 미분식이 모두 0이 되게하는 MLE 식들은 아래와 같다.

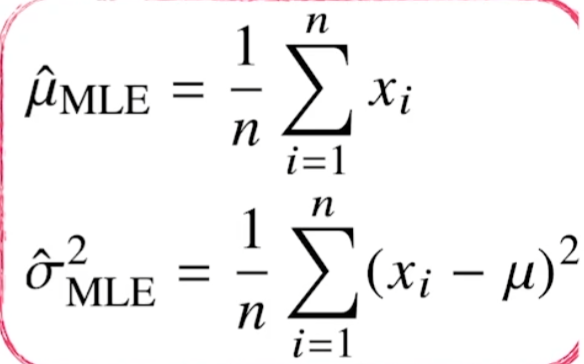
MLE에서는 불편추정량(unbiased)를 보장하지 않기에 그냥 n으로 나눈다.

카테고리 분포의 최대가능도 추정법 예제

카테고리 분포 Multinoulli(x; p1, .. pd)를 따르는 확률변수 X로부터 독립적인 표본 {x1, ... ,xn}을 얻었다고 하자.

이는 마치 one hot encoding처럼 xn은 d차원 벡터인데, 한개의 값만 1이고 나머지는 0으로 되어있다.

이 때, 카테고리 분포의 모수 (p1, ..., pd)를 추정하는 방법을 알아보자.

카테고리 분포의 모수

정규분포의 모수들은 평균과 분산과 같이 통계량이다.

카테고리 분포의 모수는 확률을 나타낸다. (p1, ... , pd)는 d차원에서 각각의 차원이 0 또는 1이 되는 확률을 가진다. 따라서 p1부터 pd까지 모두 더해주면 1이다.

정의

i번째 x의 k번째 차원에 해당하는 값을 을 k번째 모수인 p에 승수로써 계산하라는 표현이다. 이를 카테고리 분포의 MLE에서 아래와 같이 활용한다.

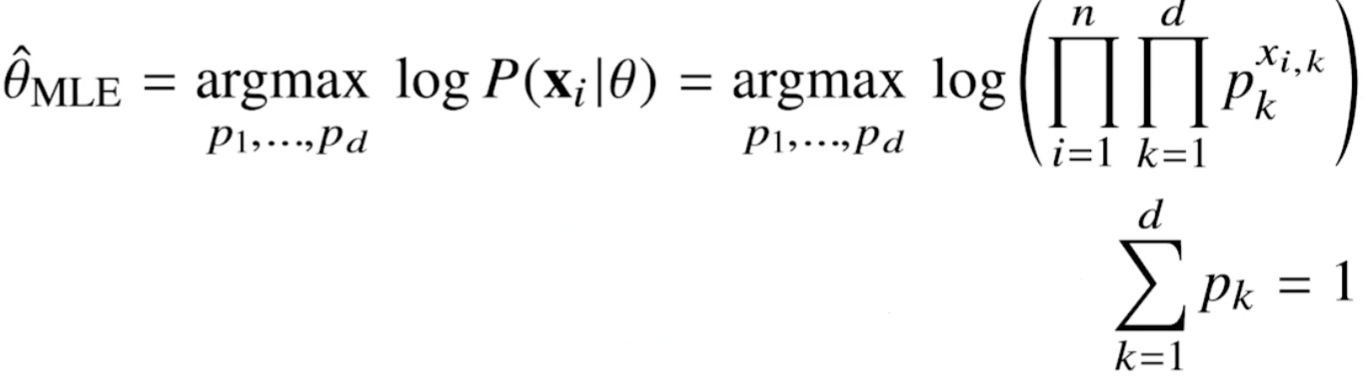
앞서 카테고리 분포의 모수를 정의할 때 언급했듯이 모든 모수 pk를 더하면 1이다.

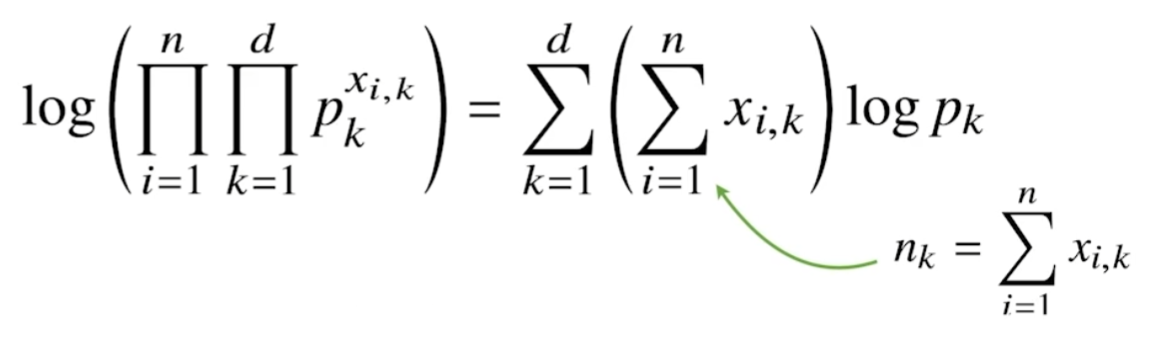
pk의 승수에 있던 내용들이 로그에 의해 앞으로 나온다.
이것을 간략하게 nk라고 표현했다.

nk는 당연하게도 주어진 주어진 데이터 xi에 대해서 k번째 차원의 값이 1인 데이터의 개수를 세는 것이다.

제약식이 있으니 제약식을 활용하여 라그랑주 승수법을 통해 목적식을 최적화한다.

이를 pk와 람다에 대해 미분한다.

미분된 두 수식 모두 0이 되어야 한다.
즉, 두 수식은 pk에 대한 식으로 한꺼번에 정리할 수 있다.

딥러니에서의 최대가능도 추정법

NN에서 가중치 Θ를 다음과 같이 정의해보자.

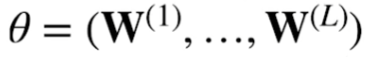
이 때, softmax 벡터는 카테고리분포의 모수 (p1, ... , pk)를 모델링한다. 이전 포스팅에서 NN의 출력단에서 softmax를 사용해 조건부확률을 구현한다고 했는데 그 확률을 마치 카테고리분포의 모수로 사용하는 것이다.