[Lv.3] 경주로 건설 - JAVA

https://school.programmers.co.kr/learn/courses/30/lessons/67259

문제 설명

건설회사의 설계사인 죠르디는 고객사로부터 자동차 경주로 건설에 필요한 견적을 의뢰받았습니다.

제공된 경주로 설계 도면에 따르면 경주로 부지는 N x N 크기의 정사각형 격자 형태이며 각 격자는 1 x 1 크기입니다.

설계 도면에는 각 격자의 칸은 0 또는 1 로 채워져 있으며, 0은 칸이 비어 있음을 1은 해당 칸이 벽으로 채워져 있음을 나타냅니다.

경주로의 출발점은 (0, 0) 칸(좌측 상단)이며, 도착점은 (N-1, N-1) 칸(우측 하단)입니다. 죠르디는 출발점인 (0, 0) 칸에서 출발한 자동차가 도착점인 (N-1, N-1) 칸까지 무사히 도달할 수 있게 중간에 끊기지 않도록 경주로를 건설해야 합니다.

경주로는 상, 하, 좌, 우로 인접한 두 빈 칸을 연결하여 건설할 수 있으며, 벽이 있는 칸에는 경주로를 건설할 수 없습니다.

이때, 인접한 두 빈 칸을 상하 또는 좌우로 연결한 경주로를 직선 도로 라고 합니다.

또한 두 직선 도로가 서로 직각으로 만나는 지점을 코너 라고 부릅니다.

건설 비용을 계산해 보니 직선 도로 하나를 만들 때는 100원이 소요되며, 코너를 하나 만들 때는 500원이 추가로 듭니다.

죠르디는 견적서 작성을 위해 경주로를 건설하는 데 필요한 최소 비용을 계산해야 합니다.

예를 들어, 아래 그림은 직선 도로 6개와 코너 4개로 구성된 임의의 경주로 예시이며, 건설 비용은 6 x 100 + 4 x 500 = 2600원 입니다.

제한사항

• board는 2차원 정사각 배열로 배열의 크기는 3 이상 25 이하입니다.
• board 배열의 각 원소의 값은 0 또는 1 입니다.
  • 도면의 가장 왼쪽 상단 좌표는 (0, 0)이며, 가장 우측 하단 좌표는 (N-1, N-1) 입니다.
  • 원소의 값 0은 칸이 비어 있어 도로 연결이 가능함을 1은 칸이 벽으로 채워져 있어 도로 연결이 불가능함을 나타냅니다.
• board는 항상 출발점에서 도착점까지 경주로를 건설할 수 있는 형태로 주어집니다.
• 출발점과 도착점 칸의 원소의 값은 항상 0으로 주어집니다.

입출력 예

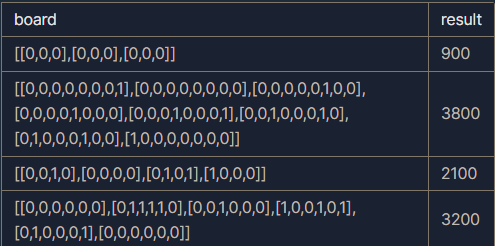
문제 풀이

미로 문제라고 하면 반사적으로 BFS 방식이 떠오른다.

하지만 해당 문제는 최단 경로를 찾는 것이 아닌 목적지 까지 도달하는데 필요한 최소 비용을 찾는 문제로 기존의 BFS 방식으로는 풀리지 않는다.

첫번째 풀이 방식

처음에는 좌표 (N-1, N-1) 까지 모든 최단 경로를 탐색할 수 있을거라 생각하여 Queue에서 꺼냈을 때 방문 처리를 하는 방식으로 cost 값을 계산했다.

하지만, 이 방식은 입출력 예제 4번에서 바로 실패가 나버린다.

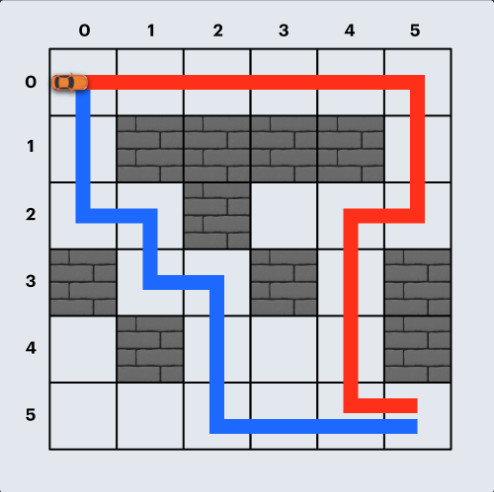
해당 그림에서 board[5][4] 부분을 도달할려고 할 때, 파란색 경로는 9번의 이동인 반면에 빨간색 경로는 11번의 이동을 통해 도달하게 된다.

따라서, 다양한 경로를 탐색하기 위해서는 단순하게 2차원 배열로 방문 처리를 하면 안된다는 것을 알았다.

두번째 풀이 방식

방문 처리를 하지 않고 DP 를 활용한 방법으로 board와 같은 크기의 memo의 모든 값을 0으로 초기화 해놓고 BFS 방식으로 다음 좌표값으로 이동할 때 memo에 기록되어 있는 cost 값이 클 때만 이동하는 방식이다.

해당 방식은 마지막 25번 테스트 케이스를 제외하고 모두 정답으로 처리된다.

처음에는 순조롭게 테스트 케이스에서 파란불이 들어오길래 다 푼줄 알고 뿌듯하게 바라보고 있었는데 마지막 케이스에서 빨간불이 들어오면서 많이 당황했다.

질문 게시판과 구글링을 해본 결과 다음과 같은 반례 케이스에서는 해당 방식으로 풀리지 않는다는 것을 알았다.

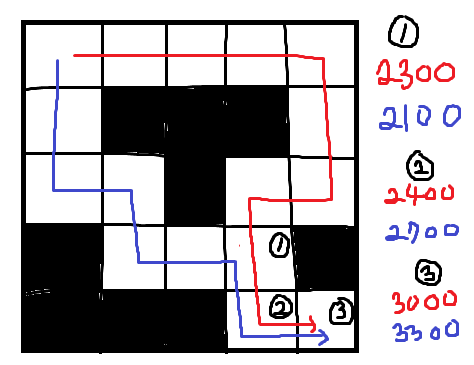
마우스로 그려서 퀄리티가 많이 떨어진다..🥹

해당 방식에 따르면 1번 위치에서 파란색 경로가 빨간색 경로보다 cost 값이 더 낮기 때문에 빨간색 경로는 1번 위치로 들어오지 못하게 된다.

하지만, 결과적으로 목표 위치인 3번 위치를 비교해 봤을 때, 빨간색 경로가 파란색 경로보다 cost 값이 더 낮아지게 된다.

세번째 풀이 방식

결론부터 말하면, 첫번째 방식을 보완하고 두번째 방식을 섞어서 해결하게 되었다.

먼저 방문 처리를 하는데 있어서 해당 경로의 방향 정보도 같이 포함해서 3차원 배열로 방문 처리를 했다.

추가로, 두번째 방식인 DP 방식을 그대로 사용하면서 해당 좌표값에서는 최솟값이 유지되도록 하였다.

풀이 코드

import java.util.LinkedList;
import java.util.Queue;

class Cell {
    int x;
    int y;
    int cost;
    int[] direction;

    public Cell(int x, int y, int cost, int[] direction) {
        this.x = x;
        this.y = y;
        this.cost = cost;
        this.direction = direction;
    }
}

class Solution {
    public int solution(int[][] board) {
        return bfs(board);
    }

    int bfs(int[][] board) {
        Queue<Cell> queue = new LinkedList<>();
        int[][] memo = new int[board.length][board.length];
        boolean[][][] visited = new boolean[board.length][board.length][4];

        int result = Integer.MAX_VALUE;

        int[] dx = {0, 0, 1, -1};
        int[] dy = {1, -1, 0, -0};

        Cell start = new Cell(0, 0, 0, new int[]{0, 0});
        queue.add(start);

        while (!queue.isEmpty()) {
            Cell cell = queue.poll();

            if (cell.x == board.length - 1 && cell.y == board.length - 1) {
                result = Math.min(result, cell.cost);
                continue;
            }

            for (int index = 0; index < 4; index++) {
                int x = cell.x + dx[index];
                int y = cell.y + dy[index];

                if (x < 0 || y < 0 || x >= board.length || y >= board.length || board[x][y] == 1) {
                    continue;
                }

                int cost = cell.cost + 100;
                if (cell.direction[0] != dx[index] && cell.direction[1] != dy[index]) {
                    cost += 500;
                }

                if (!visited[x][y][index] || memo[x][y] >= cost) {
                    visited[x][y][index] = true;
                    memo[x][y] = cost;
                    queue.add(new Cell(x, y, memo[x][y], new int[]{dx[index], dy[index]}));
                }
            }
        }

        return result;
    }
}