Union-Find 연산
여러 노드가 존재할 때 임의의 두 노드를 같은 집합으로 묶어주고, 임의의 두 노드가 한 집합에 있는지를 파악하는 알고리즘이다
Union 연산과 Find 연산 두 가지를 진행하기 때문에 이름이 Union-Find 연산이다
두 노드가 연결되어 있는지, 연결되어 있지 않은지를 판별할 수 있어서 서로소 집합(Disjoint-set)이라고도 부른다
Union 연산
여러 노드가 있을 때 특정 노드 2개를 연결해서 1개의 집합으로 묶는 연산
- 노드 2개 합치기 = union 연산
- 그래프 2개 합치기 = union 연산
Find 연산
두 노드가 같은 집합에 속해 있는지 확인하는 연산
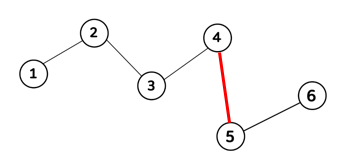한 그래프에 속한 노드들의 루트는 모두 동일하다 위의 그림에서는 6을 루트 노드로 가진다고 볼 수 있다
Union-Find 연산 코드
class VertexSets { // 정점 집합 클래스
int parent[MAX_VTXS]; // 부모 정점
int nSets; // 집합의 개수
public:
VertexSets(int n) :nSets(n) {
for (int i = 0;i < nSets;i++) {
parent[i] = -1; // 초기에 모든 정점은 root
}
}
bool isRoot(int i) {
return parent[i] < 0;
}
int findSet(int v) { // v가 속한 집합의 root를 반환
while (!isRoot(v)) v = parent[v];
return v;
}
void unionSets(int s1, int s2) { // 집합 s1을 집합 s2에 합침
parent[s1] = s2; // s1의 parent를 s2로 변경
nSets--; // 집합 2개를 합쳤으므로 집합 개수는 1 감소
}
};가중치 그래프
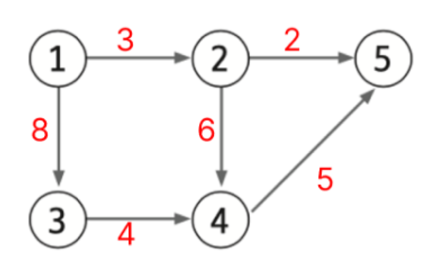간선에 가중치가 할당된 그래프다
가중치 표현 방법
Spanning Tree(신장 트리, 스패닝 트리)
1. 그래프 내의 모든 정점이 연결되어 있고
2. 사이클이 없는 트리이다
그래프의 일부 간선을 이용해서 만든 트리이기 때문에 그래프의 부분집합이다 (하나의 그래프에 Spanning Tree는 여러 개 존재할 수 있다)
또한, 사이클이 생기면 안 되기 때문에 노드가 n개일 때 n-1개의 에지로 이루어진다
MST(Minimum Spanning Tree, 최소 신장 트리)
- Spanning Tree 중에서 사용된 총 에지 가중치의 합이 최소여야 한다
- 반드시 노드가 n개일 때, n-1개의 간선만 사용해야 한다
- 사이클이 포함되어서는 안 된다 사이클이 생기는 순간 가중치의 합이 최소가 될 수 없다
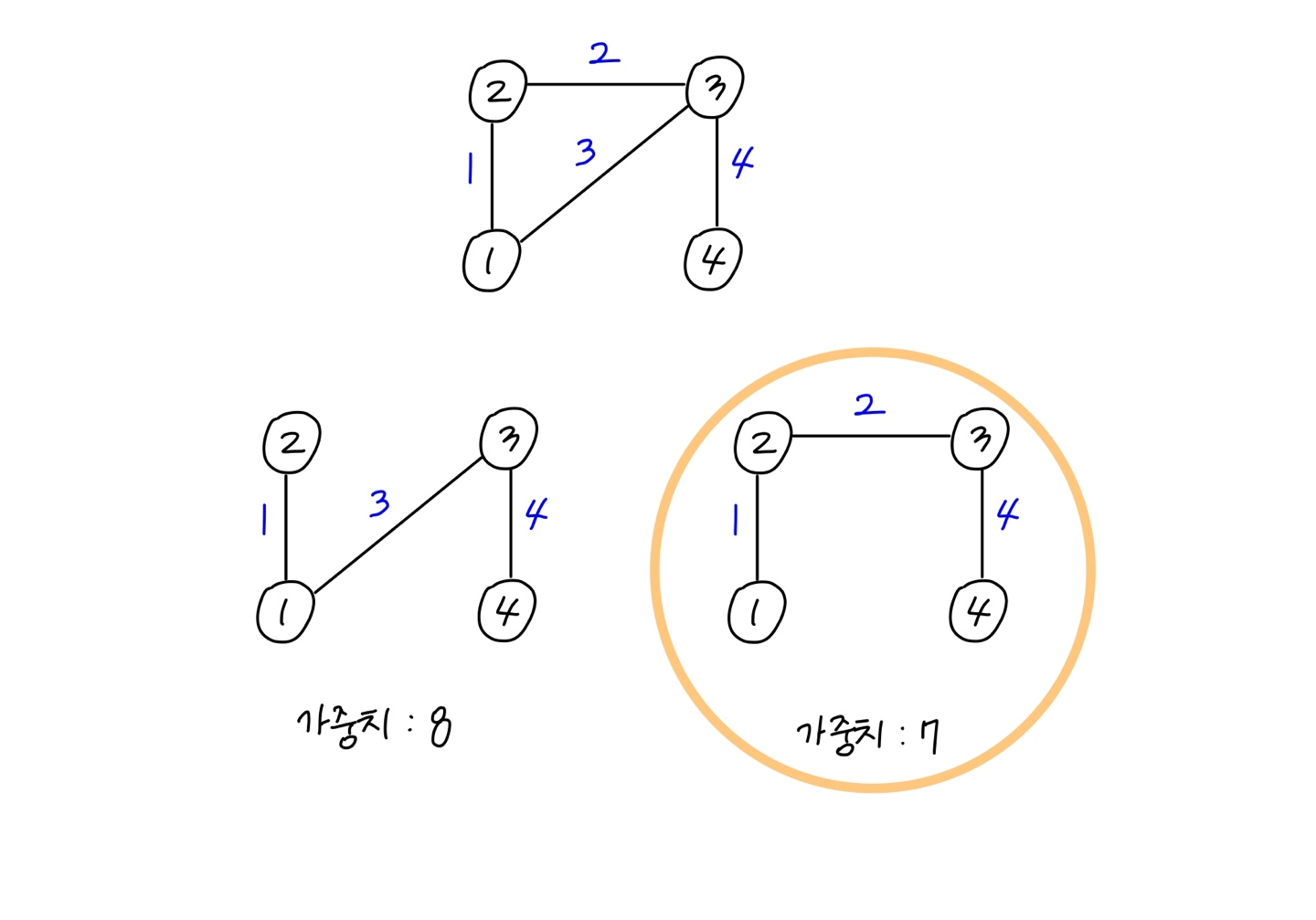
상단에 임의의 그래프가 존재할 때, 가능한 Spanning Tree는 두 개뿐이다 이 두 Spanning Tree 중 가중치의 합이 더 작은 것은 오른쪽 Spanning Tree이다 따라서 이 경우에는 오른쪽 Spanning Tree가 MST가 된다
그래프에서 MST를 구현하는 대표 알고리즘으로는 크루스칼 알고리즘과 프림 알고리즘이 있다
크루스칼 알고리즘(Kruskal Algorithm)
- 그리디 알고리즘을 사용해서 각 단계에서 가중치가 최소인 간선을 선택해서 최소 신장 트리를 만드는 알고리즘이다
- 원래 그리디는 최적의 해답을 주지 않을 수도 있는데 크루스칼 알고리즘은 최적의 해답을 주는 것으로 증명되었다
알고리즘
-
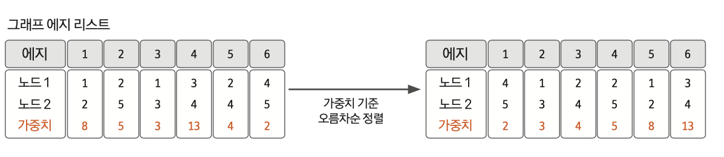
그래프의 모든 간선을 가중치에 따라 오름차순으로 정렬한다
-
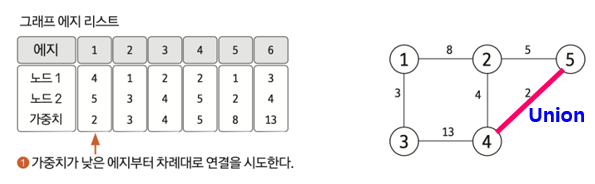
가장 가중치가 작은 간선을 뽑는다
-
이 간선을 트리에 넣을 때 사이클이 생긴다면 다시 2번으로 이동한다
-
사이클이 생기지 않으면 최소 신장 트리에 삽입한다
-
n-1개의 간선이 삽입될 때까지 2번으로 이동한다
사이클의 유무를 파악하는 방법은?
간선의 양끝 정점 두 개가 같은 집합에 속하는 경우에는 해당하는 간선을 트리에 넣으면 사이클이 발생한다 간선의 양끝 정점 두 개가 다른 집합이라면 간선을 트리에 삽입해도 사이클이 생기지 않는다
MST 코드
#include <iostream>
#include <queue>
using namespace std;
#define MAX_VTXS 10000
class VertexSets {
int parent[MAX_VTXS];
int nSets;
public:
VertexSets(int n) :nSets(n) {
for (int i = 0;i <= n;i++) {
parent[i] = -1;
}
}
bool isRoot(int n) {
return parent[n] == -1;
}
int findSet(int n) {
while (!isRoot(n)) {
n = parent[n];
}
return n;
}
void unionSets(int n, int m) {
int r1 = findSet(n);
int r2 = findSet(m);
if (r1 == r2) return;
parent[min(r1, r2)] = max(r1, r2);
nSets--;
}
};
struct Edge { // Edge 구조체 정의
int s, e, v; // 시작 노드, 끝 노드, 가중치
bool operator>(const Edge& other) const {
return v > other.v;
}
};
int main() {
int n, m; // 노드와 간선의 수
cin >> n >> m;
VertexSets vs(n);
// minHeap을 사용해서 에지를 오름차순으로 정렬
priority_queue<Edge, vector<Edge>, greater<Edge>> pq;
for (int i = 0;i < m;i++) {
int s, e, v;
cin >> s >> e >> v;
pq.push(Edge{ s,e,v }); // 에지 정보를 minHeap에 저장
}
int selectedEdges = 0; // MST에 포함되는 에지 수
int result = 0; // MST의 가중치 합
while (selectedEdges < n - 1) { // MST 에지를 n-1개 추가할 때까지만 실행
Edge now = pq.top();
pq.pop();
// 사이클이 생기는지 파악
if (vs.findSet(now.s) != vs.findSet(now.e)) { // 루트가 다르면 사이클 발생x
vs.unionSets(now.s, now.e);
selectedEdges++; // MST edge 추가
result += now.v; // MST 가중치 계산
}
}
cout << result;
return 0;
}