그래프란?
그래프는 여러 노드들이 에지로 서로 연결되어 있는 집합 상태를 의미한다 트리처럼 한 노드에 다른 노드들이 묶여있지만, 계층 구조가 아니라는 점에서 트리와 차이가 있다 (참고로 트리도 그래프의 일종이라고 볼 수 있다)
그래프 G는 (V, E)로 표시한다
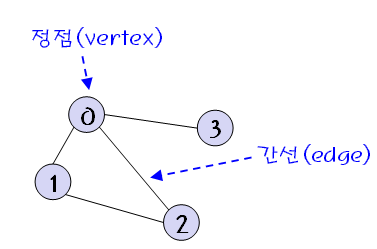
트리와 그래프의 차이
| 그래프 | 트리 | |
|---|---|---|
| 방향성 | 방향, 무방향 | 방향 |
| 사이클 | 순환, 비순환, 자기 순환 | 비순환 |
| 루트노드 | 루트 개념 없음 | 하나의 루트 존재 |
| 부모-자식 | 부모-자식 개념 없음 | 루트 노드를 제외하면 1개의 부모노드 가짐 |
| 모델 | 네트워크 모델 | 계층 모델 |
| 간선 수 | 자유 | N개의 노드를 가지면 N-1개의 간선 가짐 |
정점(vertices)
- 노드(node)라고도 부른다
- 여러 가지 특성을 가질 수 있는 객체를 의미한다
- V(G) : 그래프 G의 정점들의 집합
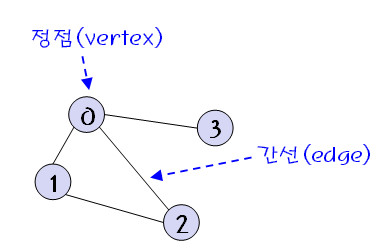ex) V = {0, 1, 2, 3}
간선(edge)
- 링크(link)라고도 부른다
- 정점들 간의 관계를 의미한다
- E(G) : 그래프 G의 간선들의 집합
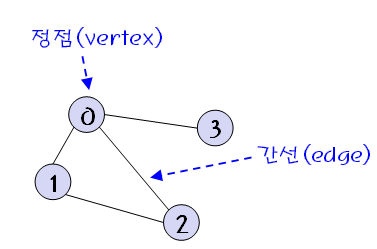
ex) E = {(0,1), (0,2), (0,3), (1,2)}
그래프 종류
Undirected graph (무방향 그래프)
Directed graph (방향 그래프)
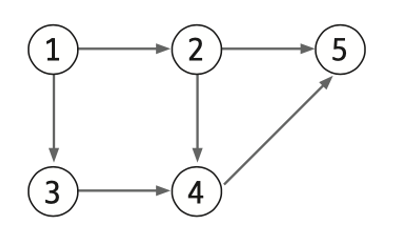
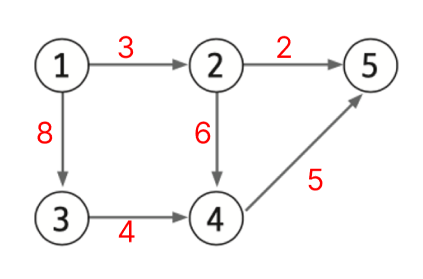
Weighted graph (가중치 그래프)
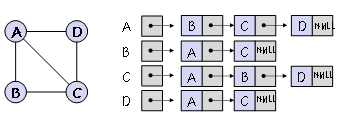
그래프 표현 방법
그래프를 표현하는 방법에는 3가지가 있으나, 이번 포스트에서는 인접 리스트를 통해서 구현하는 방법을 정리하겠다
(참고)
1. 에지 리스트
2. 인접 행렬
3. 인접 리스트
- 각 노드는 연결 리스트를 가진다
- 인접한 노드들을 연결 리스트로 표현한다
- 2차원 벡터로 그래프를 표현한다는 의미이다
undirected graph
directed graph
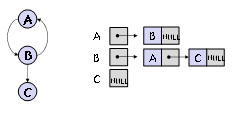
가중치 없는 그래프
N번 노드와 연결되어 있는 노드를 벡터의 위치 N에 연결된 노드 개수만큼 노드의 데이터를 push_back()하는 방식으로 표현한다
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> A; // A가 저장하는 것은 벡터
int main() {
int N, M; // N은 node 개수, M은 link 개수
cin >> N >> M;
A.resize(N + 1); // index 1~N까지 사용 (0은 사용x)
for (int i = 0;i < M;i++) {
int e1, e2; // edge (e1, e2)
cin >> e1 >> e2;
A[e1].push_back(e2);
A[e2].push_back(e1);
}
// 출력
for (int i = 1;i <= N;i++) {
cout << "[" << i << "]";
for (int n : A[i]) {
cout << "[" << n << "]";
}
cout << endl;
}
return 0;
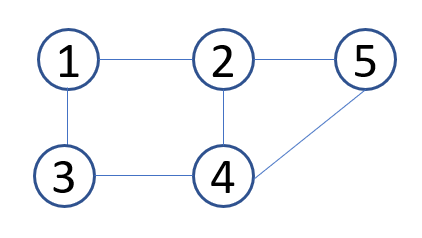
}// 입력 예시
5 6
1 2
1 3
2 4
2 5
3 4
4 5
// 출력 예시
[1][2][3]
[2][1][4][5]
[3][1][4]
[4][2][3][5]
[5][2][4]그래프 탐색
깊이 우선 탐색(DFS, depth first search)
그래프 완전 탐색 기법 중 하나다
그래프의 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친다
그 후 다른 쪽 분기로 이동하여 다시 탐색을 수행한다
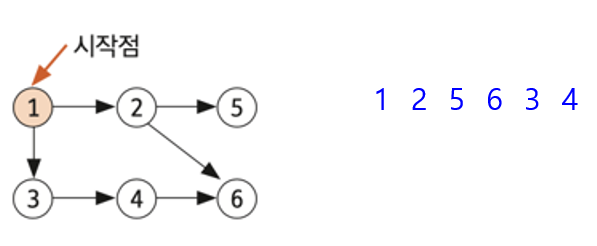마지막에 들렀던 곳을 기준으로 back해서 안 들린 곳을 탐색한다 = LIFO
DFS는 LIFO 특성을 가지므로 재귀함수를 사용하여 구현한다
또한 한 번 방문한 노드를 다시 방문하면 안 되므로 노드 방문 여부를 체크할 배열이 필요하다
void DFS(int v) { // v = 노드 번호
if (visited[v]) return; // 이미 방문했으니까 종료 (종결 조건)
visited[v] = true; // 이제 방문했으니 true로 변경
cout << v << " "; // 방문한 노드 출력
//인접 노드를 확인하는 코드
for (int i : A[v]) { // A[v]의 모든 요소가 i값으로 하나씩 들어간다
if (visited[i] == false) // 연결 노드 중 방문하지 않은 노드만 탐색
DFS(i);
}
}너비 우선 탐색 (BFS, breadth first search)
시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다 (level order traversal과 완벽하게 동일하다)
FIFO 방식으로 탐색하므로 큐를 이용해서 구현한다
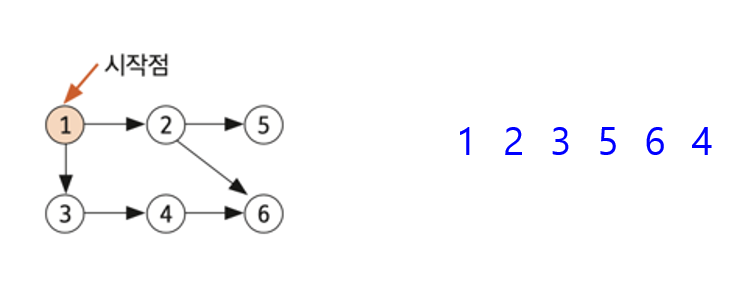DFS와 동일하게 인접 리스트로 표현하지만 큐를 사용해서 구현한다는 점에서 차이가 있다
BFS도 방문했던 노드는 다시 방문하지 않기 때문에 방문한 노드를 체크하기 위한 배열이 필요하다
#include <queue>
void BFS(int v) {
queue<int> q;
q.push(v); // 시작 정점 v를 큐에 push
visited[v]++; // 방문했음을 표시
while (!q.empty()) {
int newn = q.front();
q.pop();
cout << newn << " "; // 큐의 맨 앞 요소를 방문한 정점으로 출력
for (int i : A[newn]) { // newn의 인접 정점을 탐색
if (visited[i] == -1) { // newn의 인접 정점 중에서 방문하지 않은 경우
visited[i] = visited[newn] + 1;
q.push(i);
}
}
}
}