Discrete Cosine Transform (DCT)
DCT를 사용하는 이유
DCT는 공간 영역(Spatial Domain)에서 주파수 영역(Frequency Domain)으로 바꾸기 위해서이다. 저주파와 고주파를 분리하는 작업이기도 하다.
이미지나 영상을 주파수 영역으로 바꾸게 되면
-
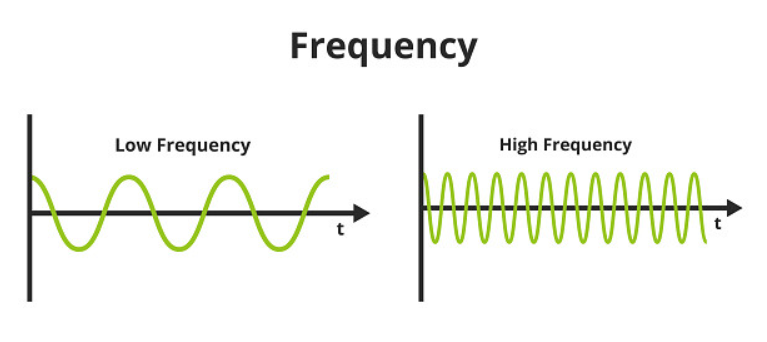
인접한 픽셀과의 차이가 작을 경우 낮은 공간주파수(자주파)를 가지고
-
인접한 픽셀과의 차이가 큰 경우 높은 공간주파수 (고주파)를 가진다
-
저주파 성분이 손실되면 인접한 픽셀과의 차지가 작았기 때문에 "큰 변화"로 인식한다
-
고주파 성분은 손실되더라도 원래 인접한 픽셀과의 차이가 컸기 때문에 "작은 변화"로 인식하게 된다
따라서 저주파 성분은 유지하고 고주파 성분을 줄이는 방식으로 진행한다
이때 저주파 성분은 유지하고 고주파 성분을 줄이는 방식으로 압축을 진행하기 위해 먼저 저주파 성분과 고주파 성분을 분리해야 하는데, 이 때 DCT를 주로 사용한다
그럼 DFT는?
DCT가 DFT의 경우보다 적은 계수로도 신호를 재생하는 능력이 좋다 -> 압축 성능이 좋다
DCT 변환식
JPEG DCT의 기준이 되는 8X8 픽셀을 기준으로 보겠다
8X8 행렬이므로 64개 값이 DCT 변환식을 거치면 64개의 DCT 계수를 얻게 된다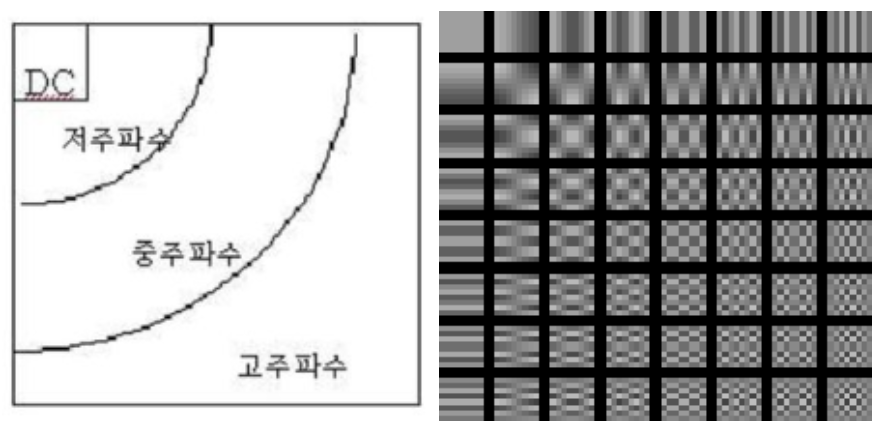
1. DCT 계수 중 가장 처음 얻는 값인 0차 계수 (0,0)는 다른 계수들과 달리 코사인 함수가 아니다 이를 DC계수 (Direct Current)라고 한다
2. 나머지 63개의 값은 AC 계수(Alternatung Current)라고 한다
DCT를 수행하게 되면 좌측 상단에 저주파 성분이 배치되고, 우측 하단에 고주파 성분이 배치된다
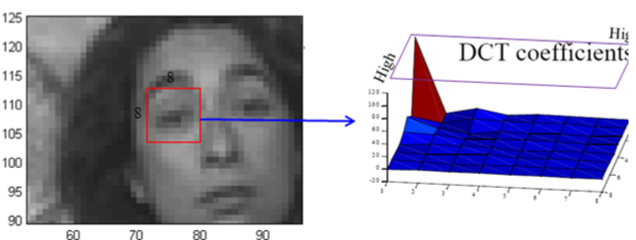우리는 대부분 저주파 영역에 몰려 있는 것을 알 수 있다 왜냐하면 대부분의 이미지는 인접한 픽셀끼리 거의 비슷한 색상으로 형성되어 있기 때문이다 저주파 성분이 많다는 의미이고, 이 성분들은 DC쪽에 몰리게 된다
Block based Discrete Cosine Transform (DCT)
1D DCT base 2D DCT
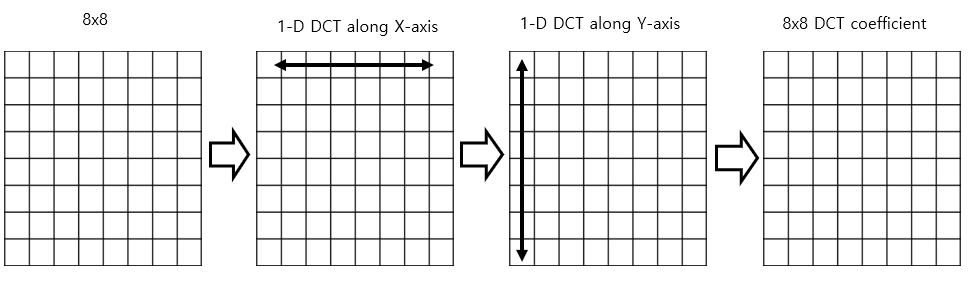1D DCT는 각각 수평/수직 방향으로 진행되고, 2D DCT도 동일하다
Fast 1D DCT
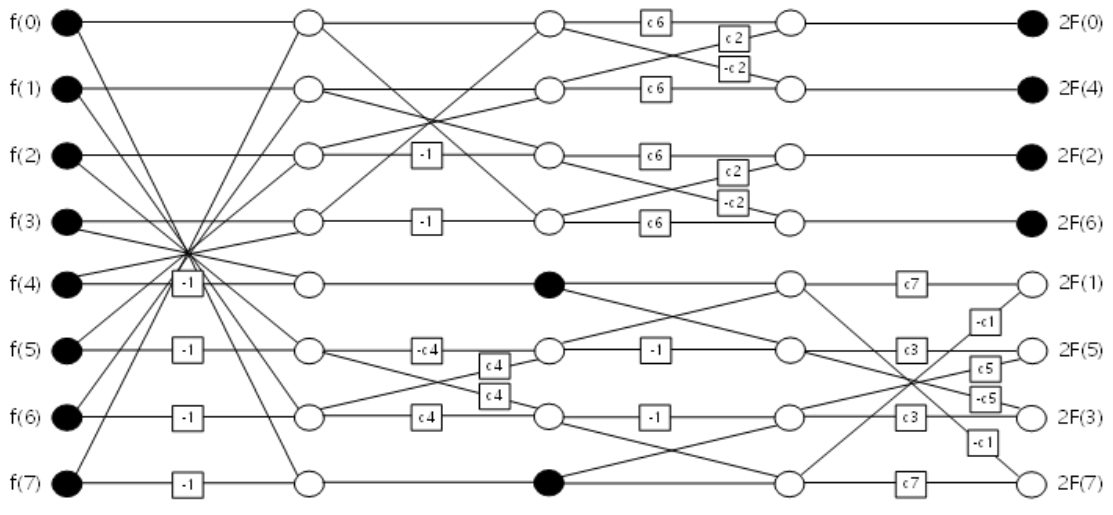-1 : -1을 곱한다
cX : cos(Xπ/16)를 곱한다
원모양 : 더한다
ex) C6 = 6π/16 = 3π/8
ex) D2 = (f(1)+f(6)) - (f(2)+f(5)) = f(1)+f(6)-f(2)-f(5)
