강의 동영상 Lecture 7: Convolutional Networks
s슬라이드 및 이미지 참고 slides

이전까지 보았던 linear classifier와 neural network model은 pixel값들을 flat하게 펄쳐 연산하였기 때문에 이미지의 공간적 정보를 살릴 수는 없었다. 공간적 정보란 예를 들면, 가까운 픽셀은 값이 비슷하거나, RGB의 각 채널은 서로 밀접하게 관련되어 있거나, 거리가 먼 픽셀끼리는 별 연관이 없는 등 3차원 속에서 의미를 갖는 본질적인 패턴을 말한다.

이전 강의에서 보았던 matrix valued backprop도 matrix form으로 연산을 하지만 결국 flat한 것과 다를바 없어 공간적정보를 커버하지 못한다. 이러한 문제를 해결하기 위해 합성곱을 사용하여 형상을 유지한다.

Convolutional Network

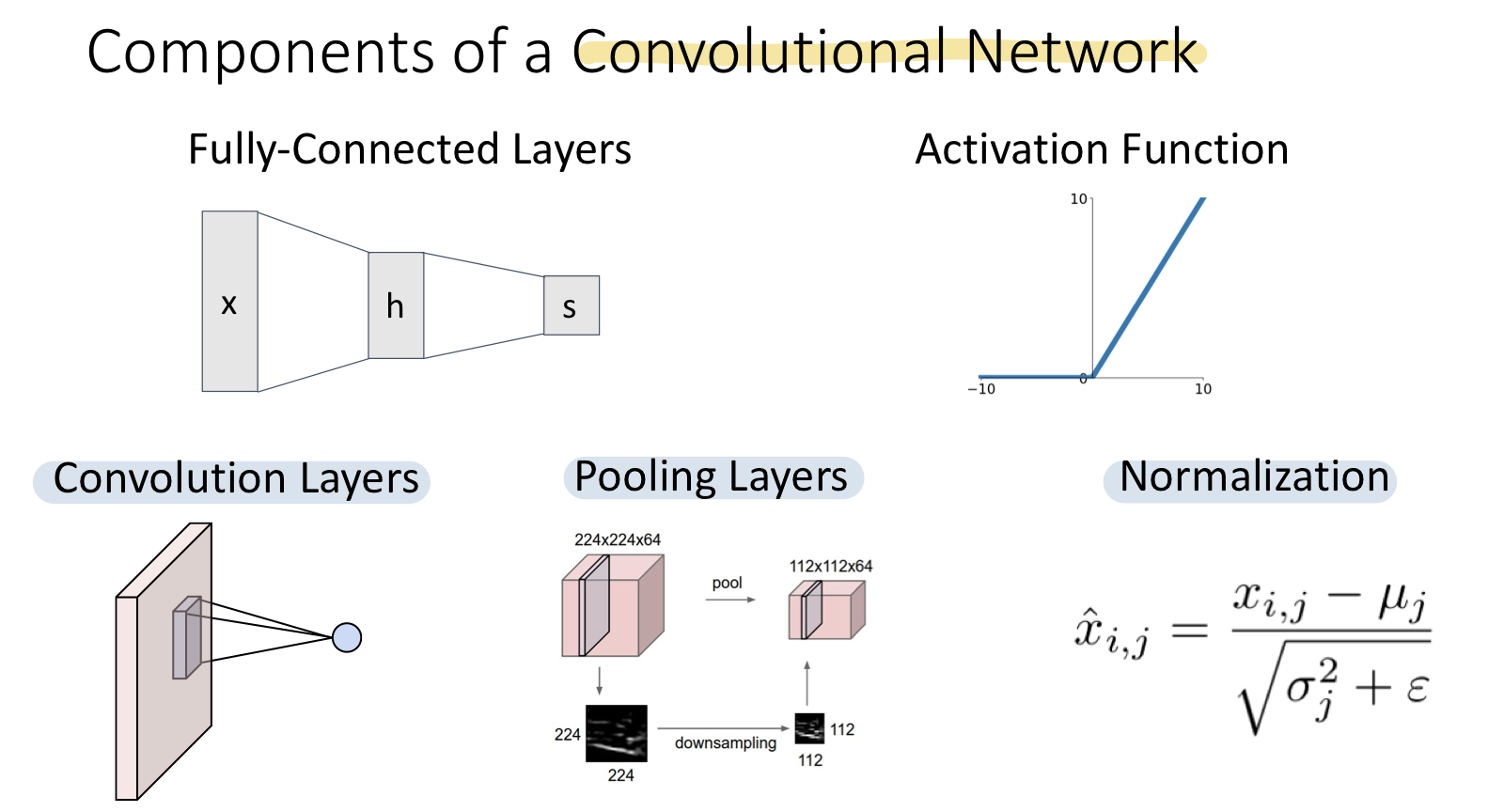
이전에 Fully-Connected Network는 Fully-Connected Layers와 Activation Function으로 구성되어 있었다. Convolutional Network에서는 계산그래프에서 사용되는 Convolution Layers, Pooling Layers, Normalization으로 구성되어 있다. 이러한 몇가지 operation은 Fully-Connected Network를 Convolutional Network형태로 변환시켜준다.

Convolution Layer

• Weight matrix는 일종의 3-dimensional spatial structure를 갖는데 이러한 weight matrix를 filter라고 한다. 문헌에 따라 커널이라 칭하기도 한다.
• 필터는 input 이미지와 같은 크기의 채널을 갖고 이미지의 모든 spatial position을 돌아다니며 dot product연산을 한다.
• 합성곱연산은 입력 데이터에 필터를 적용한다.

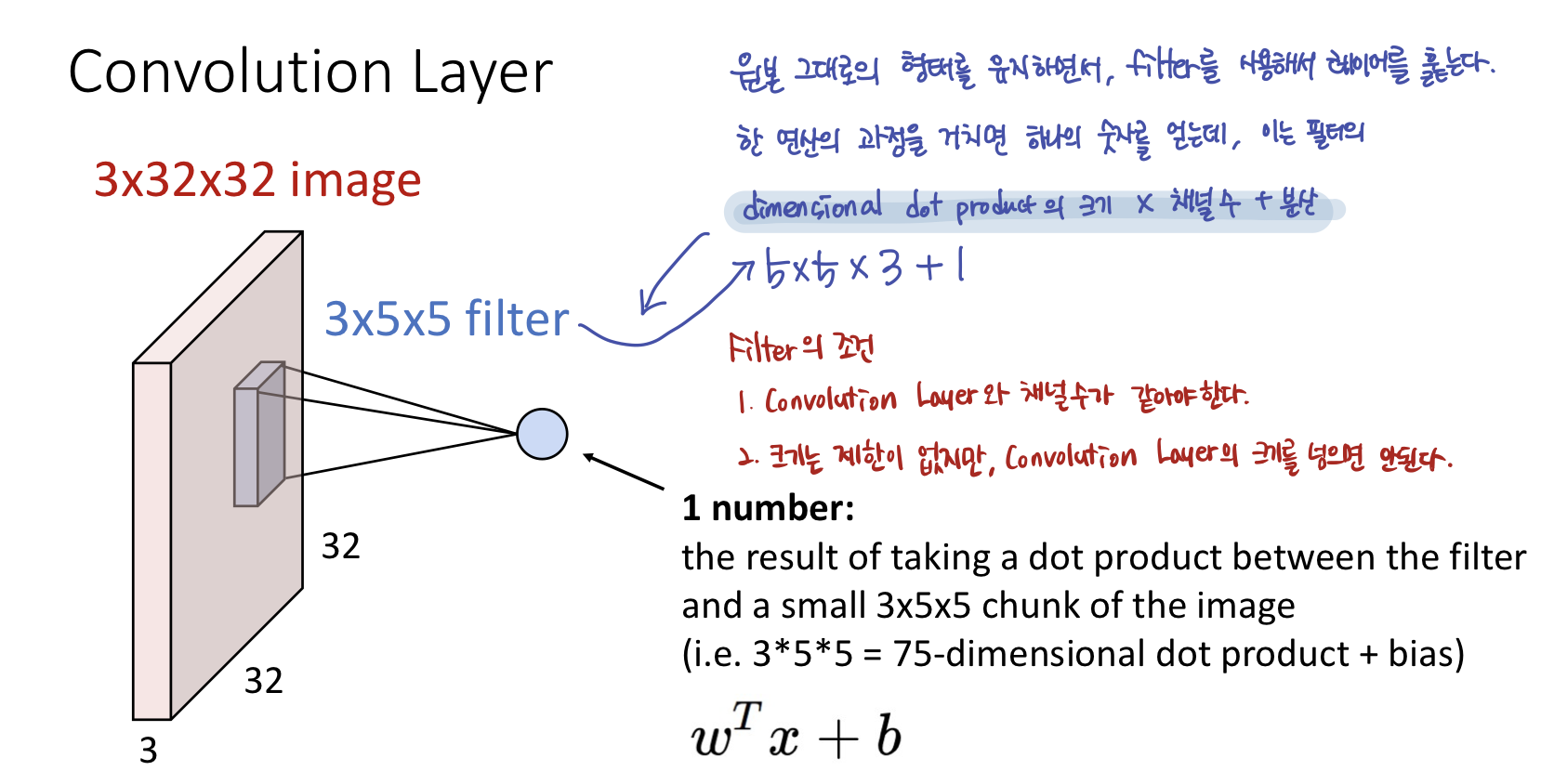
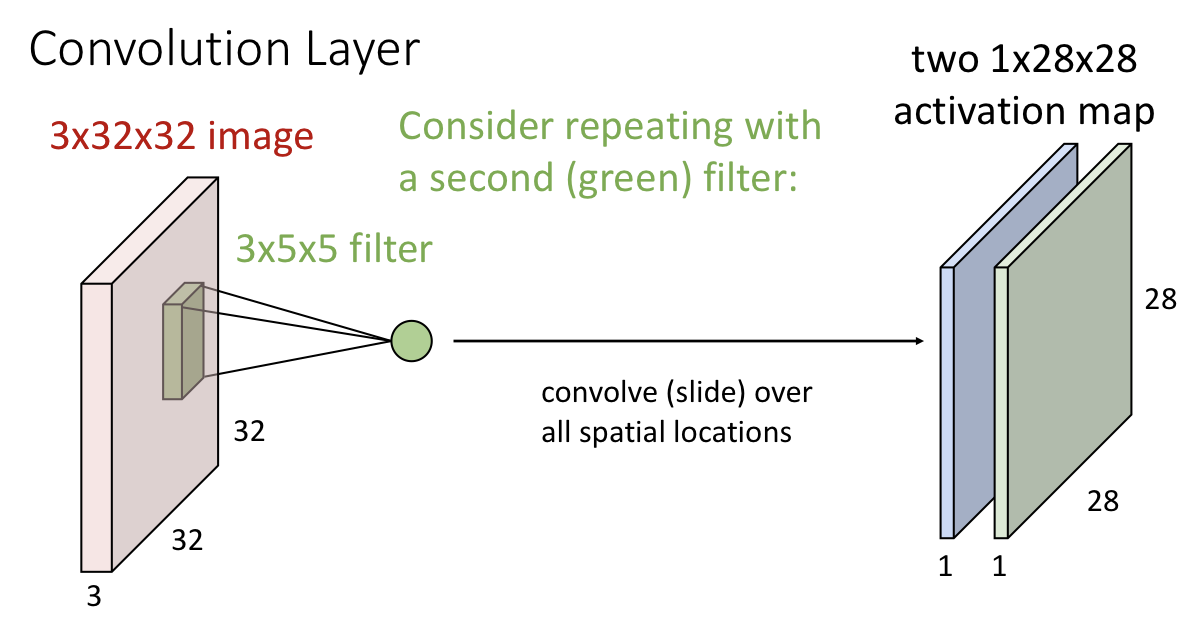
• 1개의 필터로 이러한 과정을 거치면 1채널의 activation map 1개를 얻게 되고, 필터는 각각 다른 특징을 추출한다.
• 각각의 activation map은 input 이미지의 각 spatial position이 얼마나 각각의 filter에 영향을 받았는가를 나타낸다.

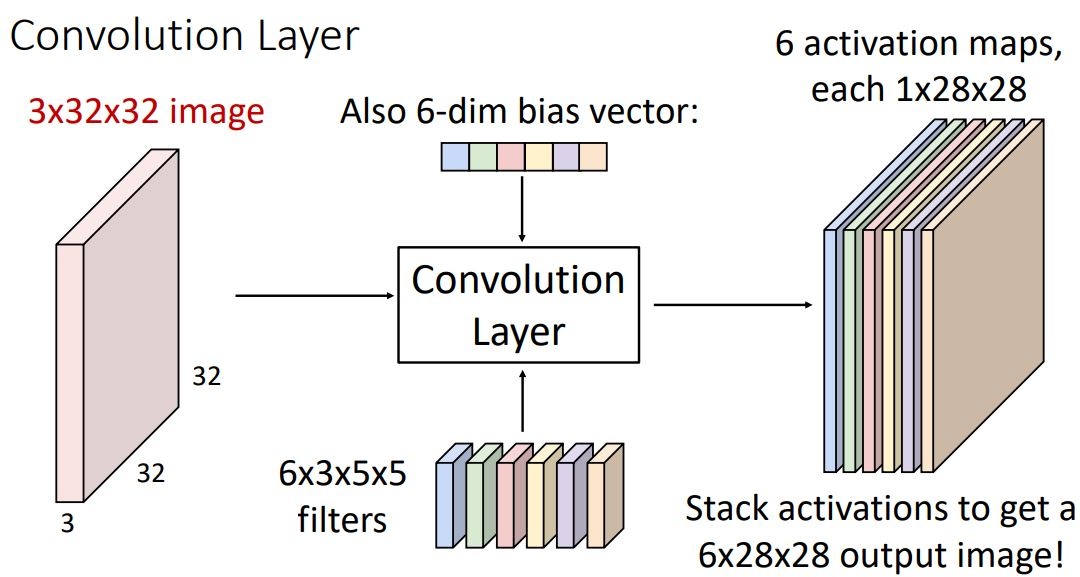
이때의 activation map들을 concatenate시켜 하나의 (depth dimension이 3인) 3-dimensional tensor로 나타낼 수 있으며 그림의 예시같은 경우 6x28x28형태를 갖게된다.

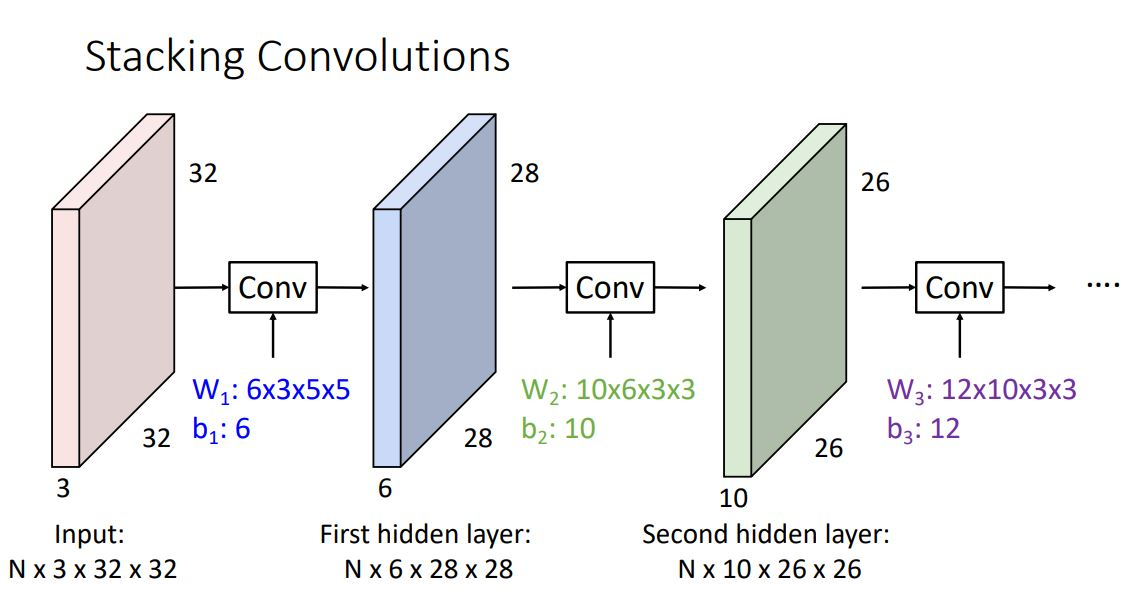
각 conv layer에있는 filter 수만큼 output이 나오게 되며 이는 다음 layer의 inout으로 들어가게 되는 형태이다. 이때 각 layer의 input과 output이 되는 activation map 들은 fully-connected network에서와 같이 hidden layer라고 말한다.

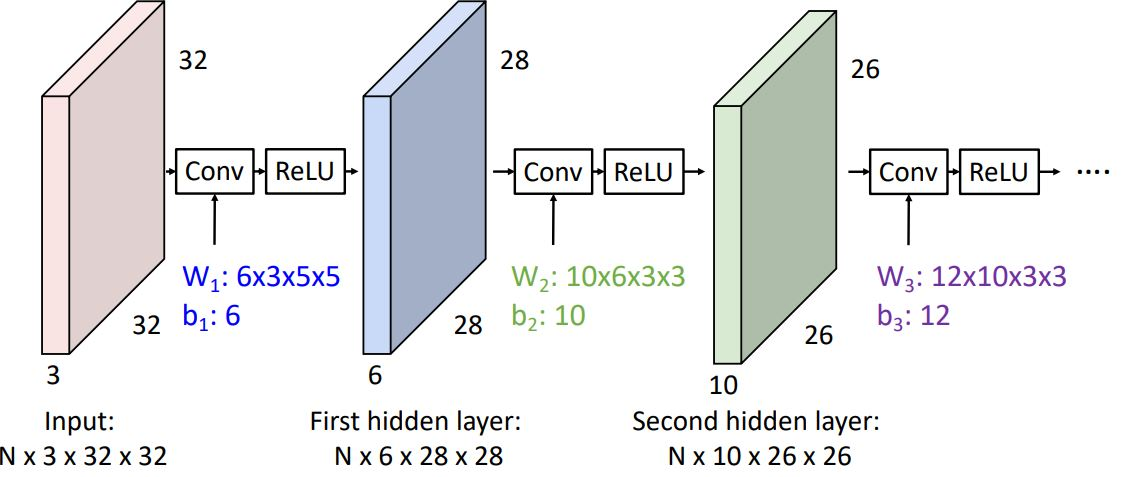
하지만 이런 형태의 convolution network는 각각의 convolution operator가 fully-connected network에서의 각 layer와 같이 linear operator에 지나지 않는다. 그렇기에 우리는 아래의 그림처럼 conv operator 직후에 (non-linear인) activation function을 취해준다.

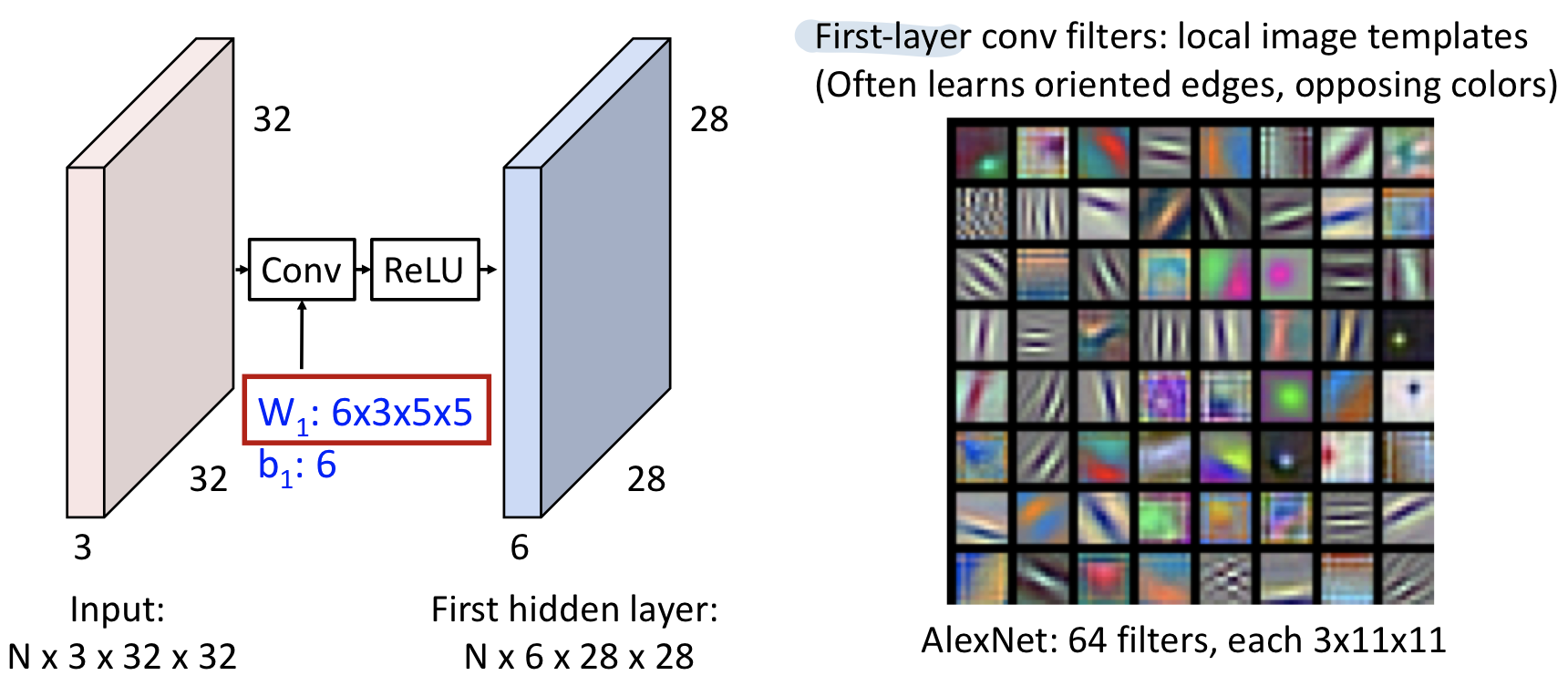
• Linear classifier는 클래스별 하나의 weight vector만 가지고 있기에 클래스별 하나의 템플릿만 가진 형태로 볼 수 있었다.
• 위의 그림은 AlexNet의 11x11 RGB image를 학습한 첫번째 layer의 filters이다. 이 각각의 filter들은 oriented edge정보와 opposing color정보 등 low-level feature를 학습한 것으로 볼 수 있다.
• 이러한 각각의 filter들은 oriented edge, opposing color로 해석되는 정보를 통해 input image의 각 position이 얼마나 다음 hidden layer에 영향을 미치는 정도를 나타낸다.
• 다른 표현으론 64-dimensional feature vector가 있고 각각의 vector는 하나의 input position에서의 64개의 feature를 학습한 형태로 생각해 볼 수 있다

In general:

• Input : W
• Filter : K
• Output : W - K + 1

input의 edge(corner) position을 커널이 커버하지 못하여 매 convolution operation을 거치면서 점점 spatial dimension이 줄면서 pixel의 손실이 일어난다. 이러한 문제를 해결하기위해 이미지에 패딩을 적용해준다.

padding

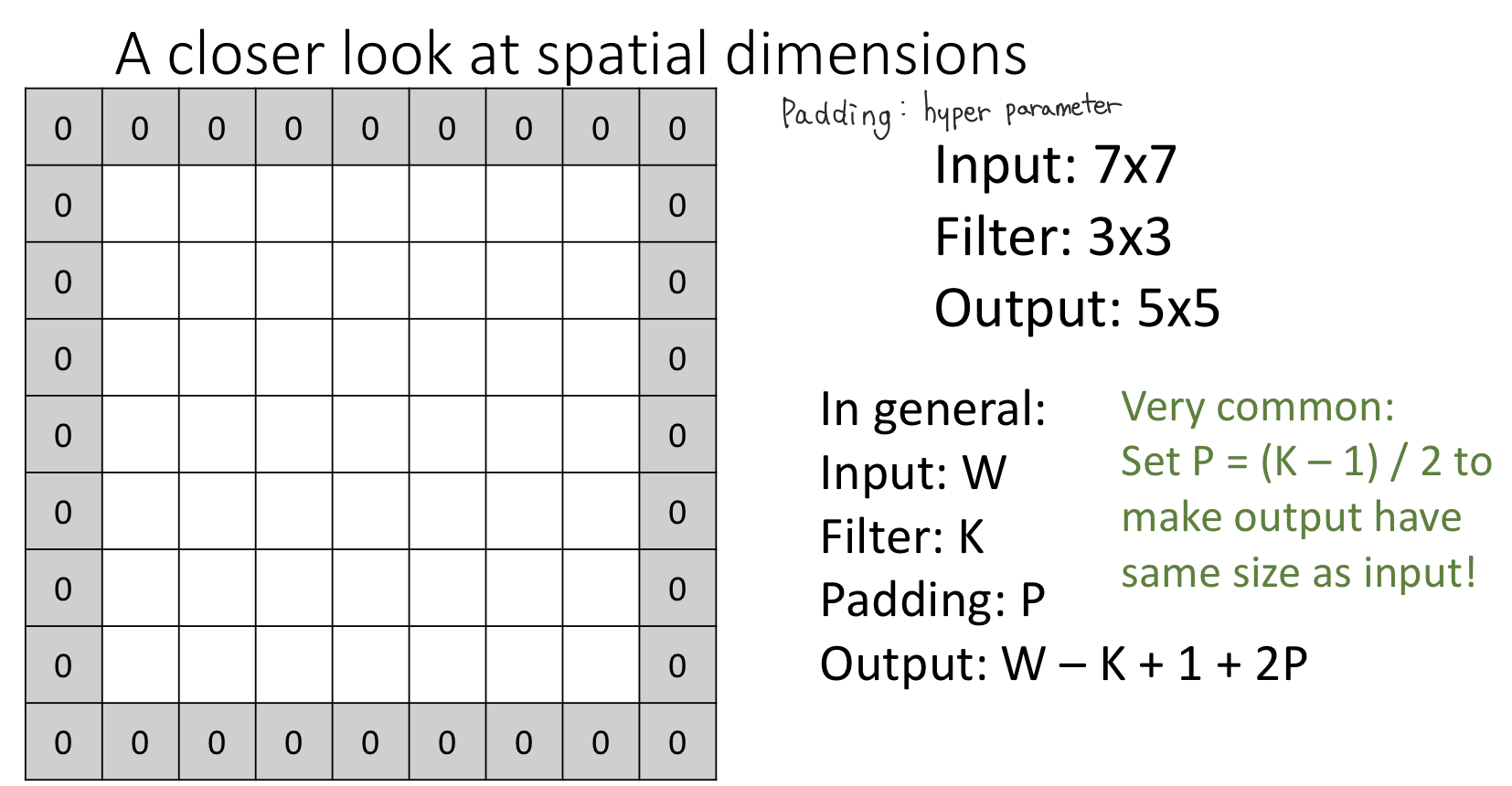
• 패딩은 주로 출력 크기를 조종할 목적으로 사용된다.
• 예를 들어 (4,4) 입력데이터에 (3,3)필터를 적용하면 출력은 (2,2)가 되어 입력보다 2만큼 줄어드는데, 이는 합성곱 연산을 몇 번이나 되풀이하는 심층신경망에서는 문제가 될 수 있다. 합성곱 연산을 거칠 때마다 크기가 작아지면 어느 시점 출력 크기가 1이 되어 더이상 합성곱 연산을 적용할 수 없게 된다. 이러한 사태를 막기위해 패딩을 사용한다.
• (4,4)패딩에 패딩 1을 적용하면 (6,6)이 되는데 이에 (3,3)필터를 적용하면 출력데이터는 (4,4)가 되어 입력데이터와 같은 크기를 유지할 수 있게 된다. 즉, 입력데이터의 공간적 크기를 고정한채로 다음 계층에 전달할 수 있게 된 것이다.
• Input image size, filter size, 추가로 stride에 따라 적용할 수 있는 padding size가 정해져있는데 stride개념을 무시했을때(stride가 1일때) 일반적으로 (K - 1) / 2 를 padding size로 사용한다.

stride

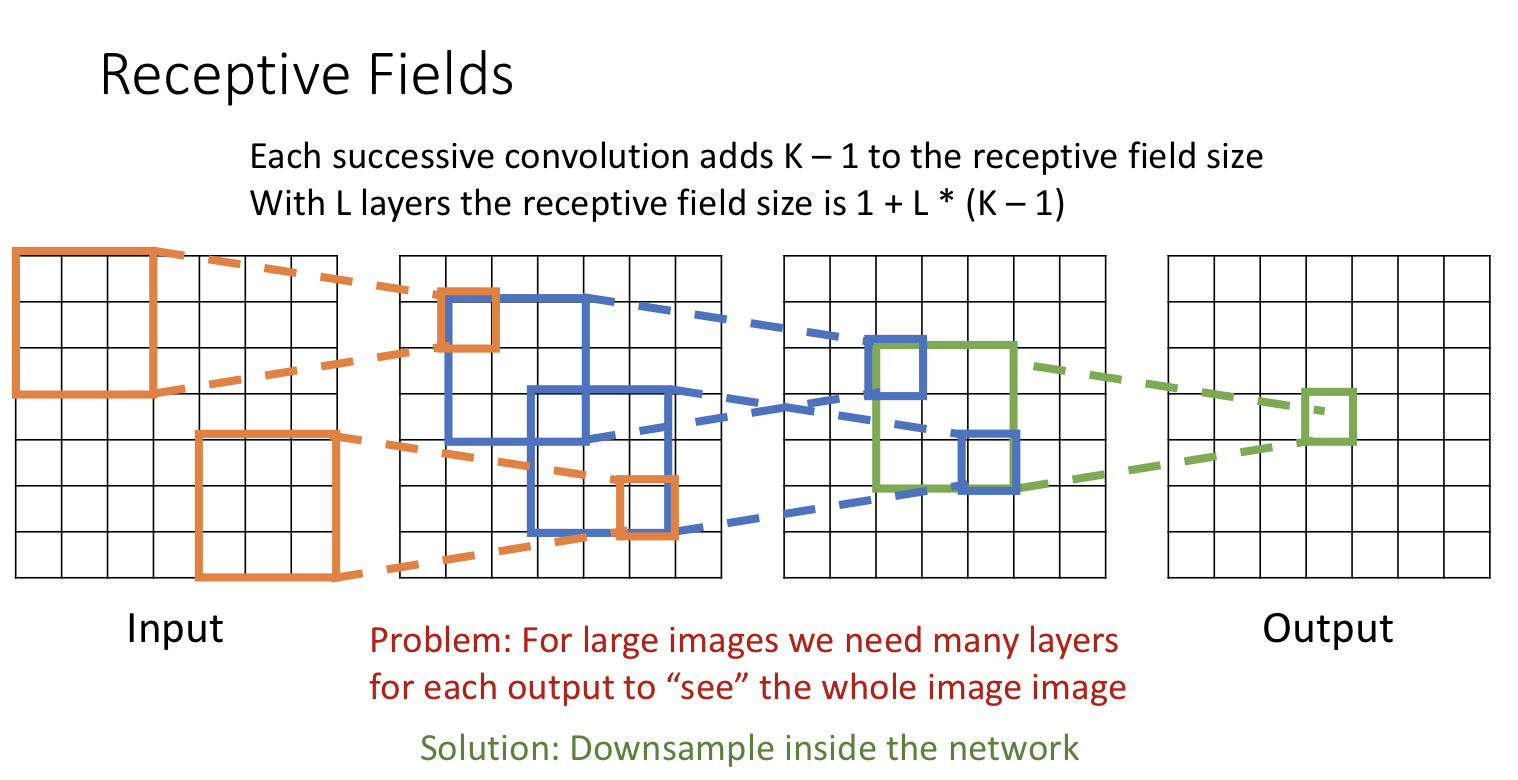
input 이미지가 커질수록 그만큼 많은 conv layer가 필요하게 된다.

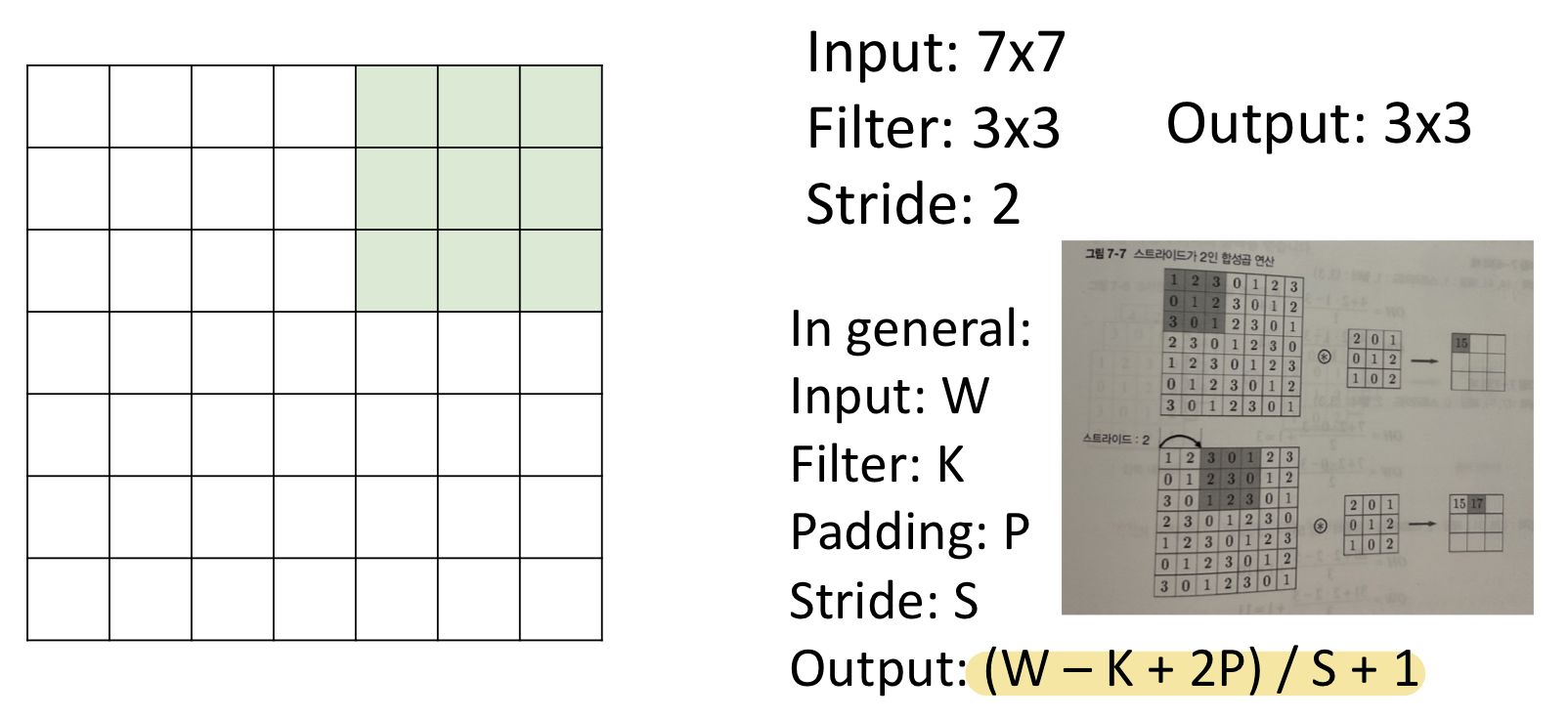
• 필터를 적용하는 위치의 간격을 스트라이드라고 한다.
• 예를 들어 스트라이드를 2로 설정하면 필터를 적용하는 윈도우가 두 칸씩 이동한다.
• 스트라이드 크기 ↑, 출력 크기 ↓

Other types of convolution

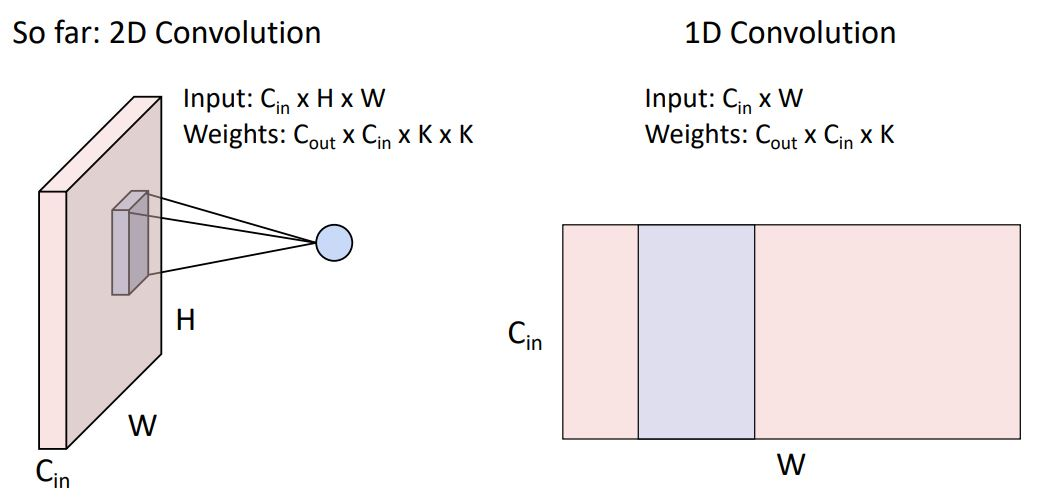
1D conv는 일반적으로 sequence형태의 textural data와 audio data에 많이 사용된다.

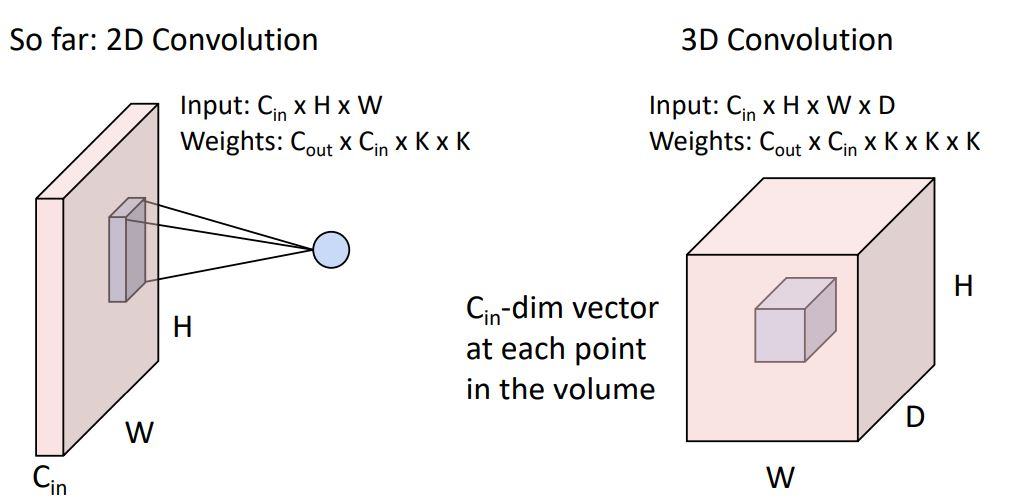
3D conv는 일반적으로 point cloud data 혹은 3d data에 사용된다.

Pooling Layer

pooling layer는 conv layer에서 stride의 역할과 비슷한 또다른 downsample방법이다.

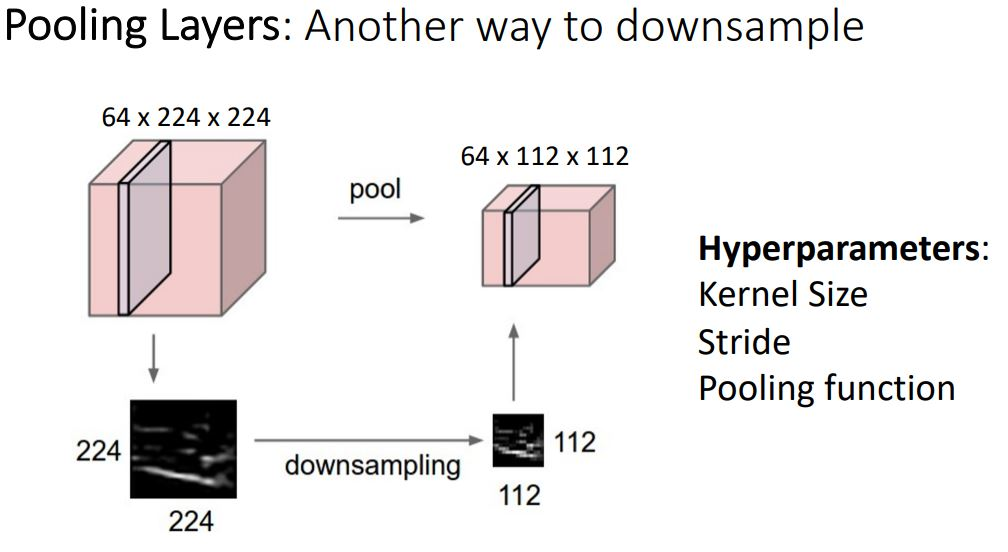
• 폴링은 세로・가로 방향의 공간을 줄이는 연산이다.
• stride와 다른 점은 학습해야할 매개변수가 없다는 점이다.
• pooling layer에서는 hyperparameter로 kernel size와 stride, pooling function만 신경쓰면 된다.
• 폴링 연산은 입력데이터의 채널 수 그대로 출력 데이터로 내보내기 때문에, 채널 수가 변하지 않는다.

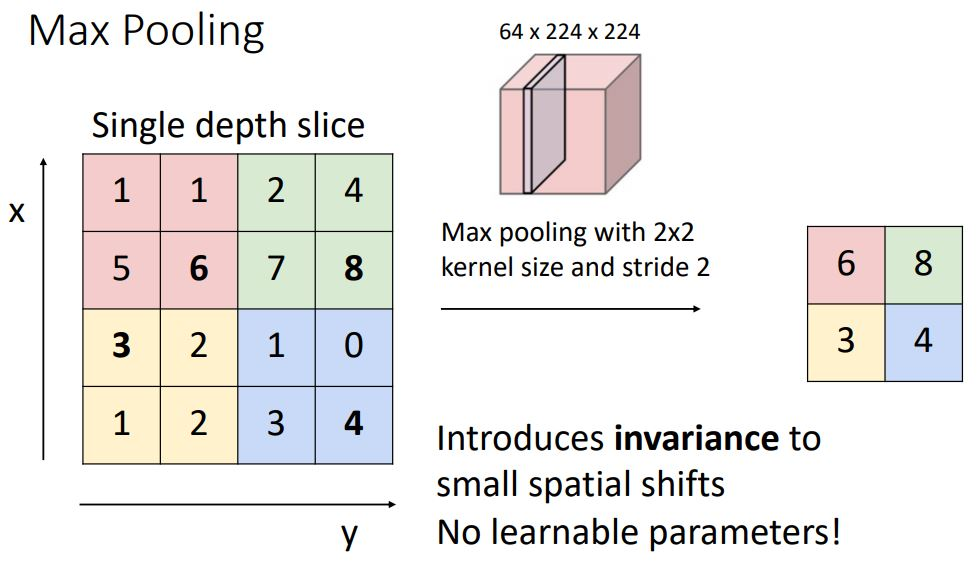
위의 이미지에서는 2x2커널사이즈와 strade가 2인 2x2 Max pooling을 하는 내용이다. 각 영역에서 가장 큰 원소 하나를 꺼내는 것이다.

참고로 풀링의 윈도우크기와 스트라이드 값은 같은 값으로 설정하는 것이 보통이다. 예를 들어 윈도우가 3x3이면 스트라이드는 3, 윈도우가 4x4이면 스트라이드를 4로 설정한다.

폴링은 max 풀링외에도 평균폴링 등이 있다. 이미지 인식 분야에서는 주로 max 풀링을 사용한다.

Normalization

Classical architecture는 매우 커지고 매우 deep해져 매우 큰 data를 학습시키 매우 힘들다는 문제가 있다. 이를 해결하기 위해 normalization 개념이 도입된다.

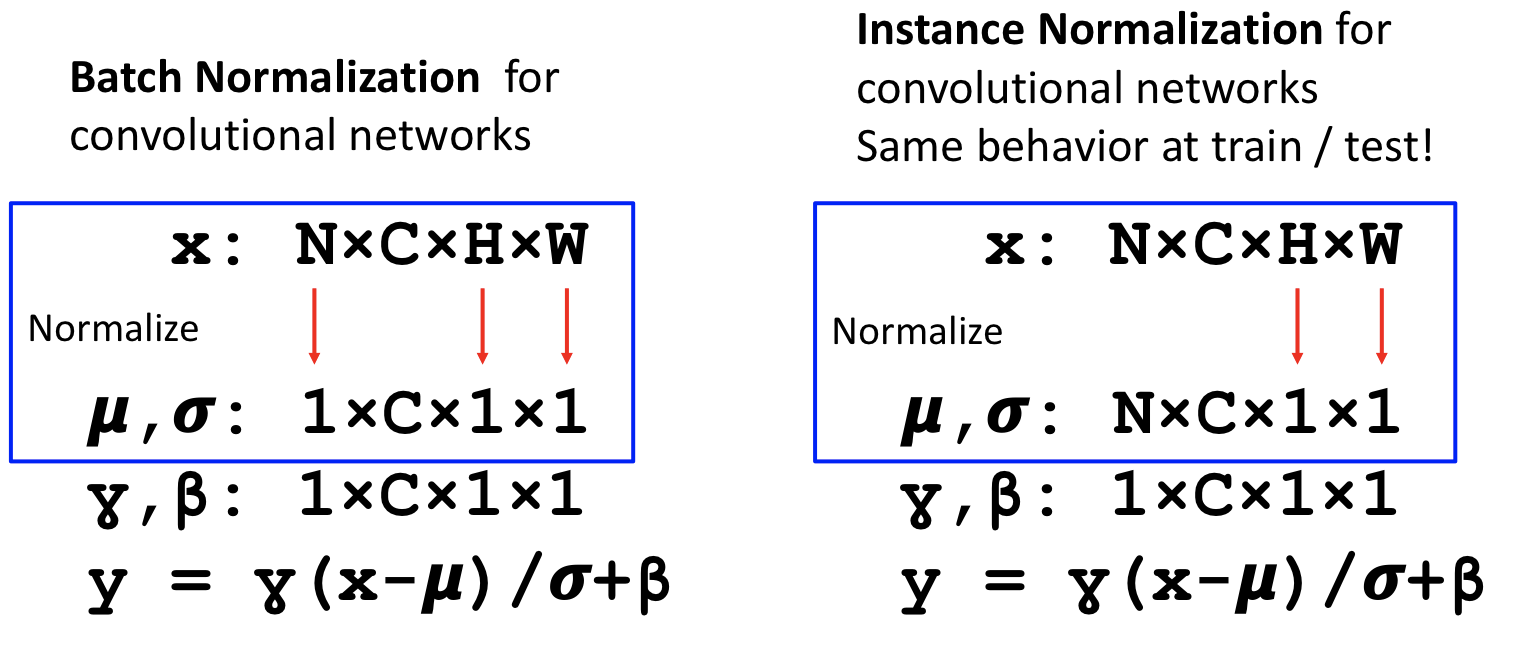
• 직전에 보았듯이 batch전체를 averaging시켜 normalize하는것은 testing 과정에서 허용되지 않는다. 그래서 Conv net에서는 Instance Normalization을 해 준다.

• Instance Normalization은 batch와 partial dimension에 averaging해주지 않고 spatial dimension에만 averaging 시켜 normalizing 해 주고. 추가로 exponentially weighted average를 적용시킨다(test시에).

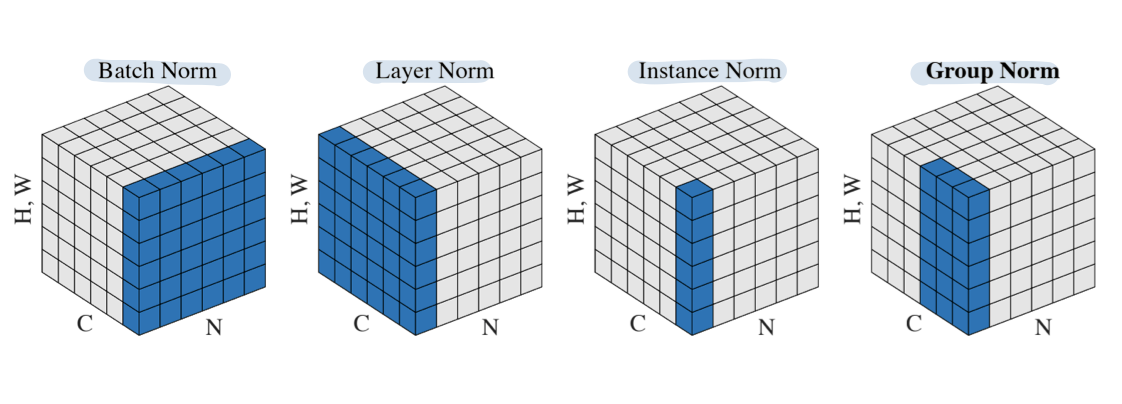
이러한 다른 type별 normalization을 그림으로 나타내면 위와 같다.

참고사이트
https://excelsior-cjh.tistory.com/180
https://aideepml.tistory.com/11
https://velog.io/@kangtae/EECS-498-007-598-005-72.-Normalization
https://warm-uk.tistory.com/47